d라이브러리

이제 본격적으로 타오가 풀었다는 콜라츠 추측에 대해 알아봅시다. 콜라츠 추측은 모든 자연수를 다음 두 조건을 따라 계산했을 때 결국 1이 된다는 추측입니다. 어떤 수가 짝수라면 2로 나누고, 홀수라면 3을 곱하고 1을 더하는 과정을 반복하면 결국 모든 자연수는 1이 될 거라는 거죠. 

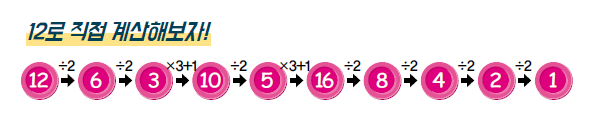
12는 9번의 과정만 거치면 1이 됩니다. 생각보다 쉽다고요? 그렇다면 27을 구해보세요.

27→82→41→124→62→31→94→…수가 계속해서 커지며 1이 될 기미가 보이지 않습니다. 27이 1이 되려면 무려 111번의 과정을 거쳐야 합니다. 그에 반해 9232는 34번 만에 1이 나오지요. 이처럼 수가 작다고 과정이 적고, 크다고 많은 게 아니기 때문에 콜라츠 추측은 풀기가 어렵습니다. 수학자들은 컴퓨터를 이용해 일일이 따져보기도 했는데요, 아주 큰 수까지 1이 된다면 콜라츠 추측이 옳을 가능성이 높으니 믿고 증명에 도전해도 되니까요. 현재 2의 68승까지 모두 성립함을 확인했습니다. 

콜라츠 추측은 누가 만들었을까?

콜라츠 추측은 울람 추측, 우박 수열, 3n+1 추측 등 다양한 이름으로 불리는데요, 그렇다면 누가 언제 떠올린 걸까요?

콜라츠 추측의 가장 오래된 흔적은 1930년대 독일 수학자 로타르 콜라츠의 공책에서 찾을 수 있습니다. 그의 공책엔 콜라츠 추측처럼 함수의 결괏값이 불규칙적으로 크게 왔다 갔다 하는 함수에 관한 메모가 여러 개 남아 있었습니다. 하지만 ‘콜라츠 추측은 이런 거야’ 하고 분명하게 적혀 있진 않았습니다. 1950년 미국 케임브리지에서 열린 세계수학자대회에 참가한 콜라츠가 콜라츠 추측을 수학자들에게 말로 설명했다고 전해지는데요, 이 역시 기록으로 남아 있진 않습니다. 

콜라츠 추측이 글로 정확하게 사람들에게 소개된 것은 1971년 영국의 기하학자 해럴드 콕서터의 강의자료라고 알려져 있습니다. 이전까지 콜라츠 추측은 수학자들의 입에서 입으로만 전해진 거죠. 당시만 해도 수학자의 관심을 끌지 못했나 봅니다. 그러다 1972년 미국 대중 과학 잡지 ‘사이언티픽 아메리칸’의 칼럼을 포함한 6개의 출판물에 등장하며 널리 알려지게 됐습니다.