d라이브러리

타오가 콜라츠 추측을 연구하게 된 계기는 놀랍게도 타오의 블로그에 올라온 익명의 네티즌의 댓글 때문입니다. 지난 2019년 8월 한 네티즌은 콜라츠 추측을 완전하게 풀려고 하기보다는 ‘거의 모든’ 숫자에 대해 풀어보자고 제안했습니다. 이 네티즌이 누군지는 모르지만, 콜라츠 추측에 대해 밝혀진 게 너무 없다 보니, 현존하는 최고의 수학자에게 ‘모든 자연수의 증명이 어렵다면 자연수 대부분이 1이라는 것을 보이자’고 이야기한 걸로 추정됩니다. 이후 타오는 정말로 콜라츠 추측을 연구했고, 의미 있는 결과를 발표했습니다. 

타오의 새로운 아이디어 시러큐스 함수

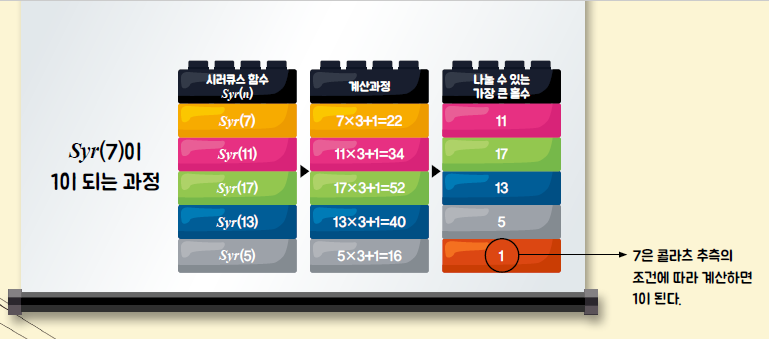
타오는 먼저 콜라츠 추측을 시러큐스 함수로 바꿔서 생각했습니다. 시러큐스 함수란 어떤 수에 3을 곱하고 1을 더한 뒤 그 수를 나눌 수 있는 가장 큰 홀수를 구하는 겁니다. 예를 들어 Syr(7)은 7×3+1=22이고 22를 나눌 수 있는 가장 큰 홀수는 11이므로 Syr(7)=11입니다. 

타오가 시러큐스 함수를 콜라츠 추측 대신 사용한 이유는 시러큐스 함수를 콜라츠 추측처럼 계속 반복했을 때 함숫값이 1이 나오면 콜라츠 추측이 반드시 성립하기 때문입니다. 직접 확인해 보면, Syr(1)은 1×3+1=4이므로 4를 나누는 가장 큰 홀수는 1입니다. Syr(5)는 5×3+1=16이므로 16을 나누는 가장 큰 홀수는 1이죠. 이처럼 어떤 수를 나눌 수 있는 가장 큰 홀수가 1이라는 것은 그 수가 2의 제곱수라는 뜻입니다. 그런데 2의 제곱수는 2로 계속 나눠져 결국 1이 되기 때문에 콜라츠 추측은 반드시 성립합니다. 그래서 타오는 콜라츠 추측을 계산 과정이 좀 더 단순한 시러큐스 함수로 바꿔 문제를 생각한 거죠. 

이제 거의 모든 자연수가 1이 되는지를 보여야 하는데요, 이전의 수학자들은 점근 밀도로 증명하려고 했습니다. 점근 밀도는 ‘1부터 100까지’ 처럼 정해놓은 수들의 모임 안에서 콜라츠 추측이 대부분 성립한다면, ‘1부터 1억까지’, ‘1부터 1조까지’처럼 수의 모임을 점점 키워 모든 자연수를 모아놓은 모임에서도 대부분 성립할 거라고 보는 방법입니다. 수학자들이 이런 확률론적 방법을 떠올렸음에도 콜라츠 추측을 해결하지 못한 이유는 점근 밀도를 구하지 못하는 상황이 많았기 때문입니다.

그래서 타오는 ‘로그 밀도’를 사용해 거의 성립하는 것을 증명했습니다. 로그 밀도는 수들의 밀도를 구하는 또 다른 방법으로, 점근 밀도보다 정확도는 떨어지지만 상황에 따라서는 점근 밀도가 구하지 못하는 밀도를 구할 수 있다는 장점이 있습니다. 결국 타오는 모든 시러큐스 함숫값이 1로 향한다는 완벽한 증명은 하지 못했지만, 어떤 함숫값이 절대 상수보다 작아진다는 것을 증명해 문제를 거의 해결한 겁니다. 

오랜 기간 방향성조차 찾지 못한 문제였기 때문에 타오의 이번 연구는 매우 의미가 있습니다. 하지만 아직 완전한 해결을 위해선 갈 길이 멀어 보입니다. 문제 자체는 너무나 쉬운만큼 풀고 싶은 욕구가 더욱 강해지는 콜라츠 추측! 에르되시 팔의 말처럼 ‘우린 아직 이 문제를 풀 준비가 되지 않은 것’일까요? 여러분이 한번 도전해보면 어떨까요?