다음은 수학자도 못 푼 수수께끼를 푼 아마추어 수학자를 소개…. 어라? 그런데 라이스 씨가 어디 가셨죠? 예? ‘문제 해답은 찾아줄 수 있지만 난 찾지 마세요’ 하고 숨으셨다고요? 이런! 비탈 씨도 나라를 지키느라 바쁘다고 하셨는데 말이죠. 디저트라도 먹으면서 이분들 얘길 하며 기다릴까요?

아마추어 수학자가 많은 건 알겠는데, 진짜 아마추어 수학자가 대단한 발견을 할 수 있는지 의심스럽다고요? 웬걸, 때로는 수학자조차 풀지 못했던 문제를 아마추어 수학자가 풀기도 하는 걸요.
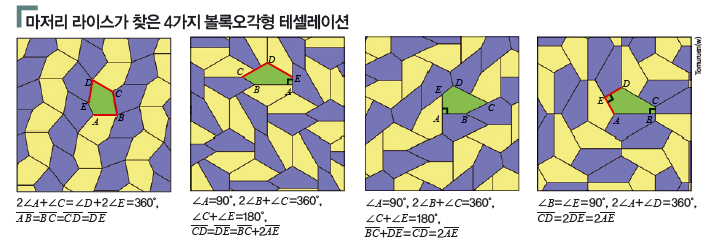
미국 샌디에이고에 살던 주부 마저리 라이스는 과학 잡지 ‘사이언티픽 아메리칸’에서 흥미로운 문제를 발견했어요. 볼록오각형을 겹치지 않게 빈틈 없이 이어 붙여 평면을 다 덮는 ‘테셀레이션’에 관한 것이었죠. 당시 볼록오각형 테셀레이션 방법은 8개뿐이었어요. 처음 볼록오각형 테셀레이션 방법 5가지를 소개한 독일 수학자 칼 라인하르트는 앞으로 테셀레이션이 몇 개나 더 있을지 알 수 없다고 했고, 라인하르트 다음으로 3가지 방법을 더 찾은 리처드 커쉬너 박사는 이 8가지가 전부일 거라고 말했죠.
라이스는 이 문제가 재미있어 보였어요. 정말 8개뿐일까 궁금했고요. 그래서 새로운 무늬를 찾기 시작했지요. 수학을 제대로 배우지 않아서 용어나 기호를 잘 몰랐던 라이스는 자기만의 표기법을 만들어서 테셀레이션을 연구했어요. 그로부터 몇 달 뒤, 새로운 테셀레이션 방법을 4가지나 찾았어요! 전문가가 확인한 결과, 그 내용은 정확했지요.
2017년 7월 프랑스 국립연구소의 미카엘 라오 박사가 볼록오각형 테셀레이션 방법이 오직 15가지밖에 없다는 사실을 컴퓨터를 이용해 증명했으니 라이스는 칼 라인하르트를 빼면 수학자들보다 테셀레이션을 더 많이 찾은 셈이에요. 슈퍼컴퓨터를 쓴 것도 아닌데 수학자를 앞섰다니 대단하죠?
독학한 아마추어 수학자가 어려운 문제를 해결했다는 사실은 미국 전역에 널리 퍼졌어요. 하지만 라이스는 수줍음이 많아 강연이나 발표를 대부분 거절했다고 하네요. 이만하면 자랑 좀 해도 될 텐데 말이에요~.
수학자도 못 푼 문제 해결한 군인
라이스 말고도 수학자가 끙끙 앓았던 어려운 문제를 푼 아마추어 수학자가 또 있어요. 이탈리아
군인이었던 지오다노 비탈이에요.
유클리드가 기원전 3세기에 집필한 ‘원론’에는 다섯 개의 공리가 있어요. 그런데 다섯 개 중 네개는 무척 명확했던 반면, 마지막 ‘평행선 공리’는 뭔가 미심쩍어 보였죠. 수학자들은 명확한 네 가지 공리로 마지막 평행선 공리를 증명할 수 있지 않을까 생각했어요.
공리★
어떤 명제를 증명하기 위해 전제로 쓰는 기본적인 가정
19세기에 니콜라이 로바쳅스키, 카를 가우스, 보여이 야누시가 평행선 공리가 성립하지 않는 ‘비유클리드 기하학’을 증명하기 전까지, 시대마다 가장 뛰어난 수학자들이 평행선 공리 증명에 도전했어요. 그리고 번번히 실패를 겪었죠.
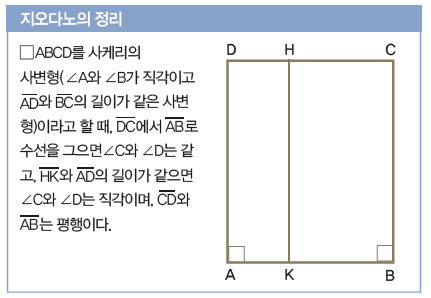
비탈도 평행선 공리에 도전했던 사람 중 하나였어요. 그리고 ‘지오다노의 정리’를 만들어 페르시아 수학자 오마르 하이얌 이후 600년간 제자리였던 평행선 공리를 한 단계 발전시키는 데 성공했어요.

김영욱 고려대학교 수학과 교수는 “현대 관점에서 보면 ‘지오다노의 정리’가 완벽하지는 않지만, 내로라하는 수학자들이 오랫동안 실패했던 문제를 아마추어가 한 단계 발전 시켰다는 건 의미가 있다”라고 말했어요.
▼관련기사를 계속 보시려면?