d라이브러리

실험 방법을 자세하게 소개할게요. 먼저 모나리자 그림을 복사해서 똑같은 그림 두 장을 만들어요. 원본과 복사본을 위아래로 포개면 각 그림을 이루는 모든 점은 자기 자신과 포개져요.

이제 원본은 그대로 두고 복사본을 마음껏 변형해요. 그림을 찢을 수는 없지만 회전하거나 구길 수 있어요. 그 다음 복사본을 다시 원본 위에 놓아 봐요. 여전히 포개지는 점이 있을까요? 포개지는 점이 생길 수 없게 모나리자를 구길 수 있을까요?

네덜란드의 수학자 라위트전 브라우어르는 모나리자를 어떻게 구겨도 원본 위의 점과 복사본 위의 같은 점이 포개지는 경우가 반드시 있다는 것을 증명했어요. 그래서 이 이론을 ‘브라우어르의 고정점 정리’라고 부르지요. 이 정리가 참인지 어떻게 알 수 있을까요?

브라우어르의 고정점 정리는 논리적으로 짝꿍인 정리가 있어요. 바로 1887년에 카미유 조르당이 증명한 곡선 정리예요. 두 정리는 어느 한쪽이 참이면 다른 쪽도 참이어야 하는 사이랍니다. 즉, 조르당의 곡선 정리가 참이면 모나리자 그림은 어떻게 구겨도 적어도 한 점에서는 원본과 겹칠 수밖에 없다고 말할 수 있어요.

논리적인 짝꿍을 보라
‘평면 위에 시작점과 끝점이 같고 중간에 교차하지 않는 곡선을 그리면 평면이 안쪽과 바깥쪽으로 나뉜다’가 조르당이 증명한 곡선 정리랍니다. 당연한 이야기 아니냐고요? 맞아요. 조르당의 곡선 정리는 참이에요. 하지만 시작점과 끝점이 같은 ‘모든’ 곡선이 그렇다고 증명하기는 쉽지 않아요. 아래쪽 미니실험을 보세요. 시작점과 끝점이 같은 미로가 한눈에 보기에도 평면을 안과 밖으로 나누나요? 그렇다면 어디가 안이고 어디가 밖인지도 쉽게 알 수 있어야 해요.

수학에서 말하는 정리는 어떤 경우든 참이어야 논란이 없기 때문에 수학자들은 당연히 맞는 것처럼 들리는 말도 수학적인 언어로 엄밀하게 증명하려고 노력해요. 이렇게 증명된 조르당 곡선 정리와 브라우어르의 고정점 정리는 그 밖의 다양한 정리를 수학적인 언어로 증명하는 데 다시 쓰입니다.

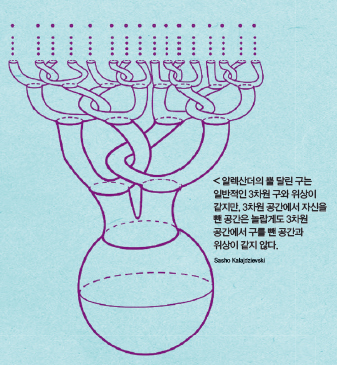
마지막으로 이러한 노력이 빛을 발한 사례를 하나 더 소개할게요. 바로 ‘알렉산더의 뿔 달린 구’! 3차원 공간을 안과 밖으로 나누는 이 구는 직관을 비껴가는 독특한 성질을 가지고 있답니다.