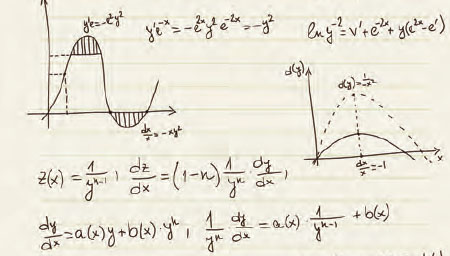d라이브러리

자기 모순에 빠진 인공지능은 프로그램을 무한히 실행한다. 보통 프로그램이 정상적으로 종료되지 않으면 컴퓨터는 화면에 ‘프로그램이 응답하지 않습니다’라는 메시지를 띄운다. 이 프로그램이 소비하는 에너지가 아깝다면 ‘일정 시간 뒤에도 작동하는 프로그램은 스스로 종료하라’는 명령을 입력할 수는 있다. 그러나 이것만으로는 인공지능이 자기 모순을 해결했다고 말하기 어렵다. 인공지능에게는 모순이 발생하는 이유에 대한 더욱 근본적인 정보가 필요하다.

모순 피하는 인공지능 설계법
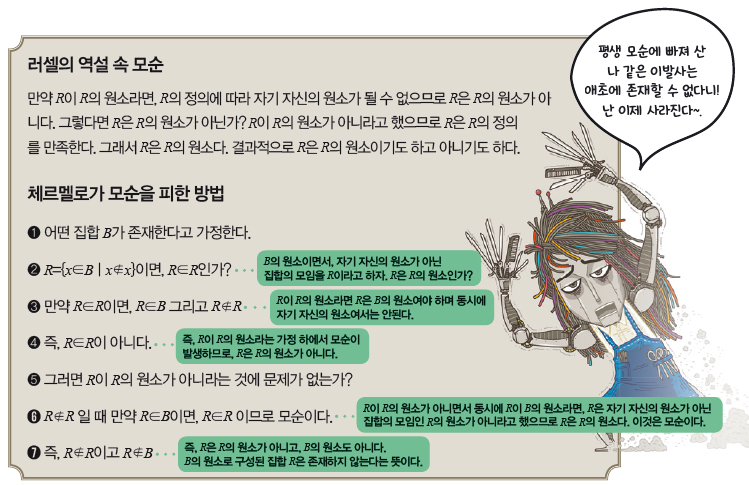
이발사의 역설은 수학자 버트런드 러셀이 스스로 고안한 집합과 원소에 관한 역설인 ‘러셀의 역설’을 설명하기 위해 1918년에 만들어낸 이야기다. 러셀의 역설을 프로그래밍한다면 왼쪽의 논리식처럼 인공지능이 무한히 실행하는 프로그램이 된다. 그런데 아주 간단한 방법으로 러셀의 역설에서 생긴 모순을 피해 다른 결론을 내리는 인공지능을 만들 수 있다.

모순을 피해갈 방법을 마련한 사람은 독일의 수학자 에른스트 체르멜로다. 체르멜로는 새로운 집합에 관한 전제 조건을 하나 추가하는 간단한 방법으로 사람들이 자주 맞닥뜨리는 모순을 피해갔다. 이로써 인공지능도 ‘집합 R이 R의 원소이기도 하고, 원소가 아니기도 하다’는 결론의 허점을 기계가 이해할 수 있는 언어로 쓸 수 있다.

그럼 이발사의 역설에서는 어떤 결론을 얻어낼 수 있을까? 자신의 머리를 스스로 자를 수 없는 모든 이의 머리는 잘라주지만 머리를 스스로 자르는 이의 머리는 잘라주지 않는 이발사는 결국 존재하지 않는다. 그 이발사가 아무리 뛰어난 인공지능일지라도.

인공지능도 ‘불완전성의 정리’는 못 이겨
이 방법대로라면 세 번째 유형의 역설도 나름대로 해결할 수 있는 인공지능을 만들 수 있다. 그렇다면 언젠가는 모든 역설을 해결할 수 있는 인공지능도 만들 수 있지 않을까? 그건 불가능하다. 20세기 수학자 쿠르트 괴델이 내놓은 ‘불완전성의 정리’ 때문이다.

괴델은 자연수에 관한 대부분을 이해하는 논리적인 시스템을 만들고자 했다. 괴델은 ➊오류를 일으키지 않고, ➋덧셈과 곱셈을 설명할 수 있으며, ➌어떤 명제를 입력받았을 때 공리★인지 아닌지를 유한 시간 안에 알아볼 수 있는 시스템이 논리적으로 잘 짜인 시스템이라고 가정했다. 그러나 불완전성의 정리는 이 시스템이 자연수에 관한 모든 명제의 참거짓을 결정할 수는 없다는 것이다. 현대 수학계는 괴델이 증명한 불완전성의 정리를 참으로 받아들인다.

불완전성의 정리에 따르면, 참인지 거짓인지 결정되지 않은 역설 또는 미해결 난제는 인공지능도 해결하기 어렵다. 과연 그런 문제가 남아있을까? 김병한 연세대학교 수학과 교수는 아직 참거짓을 판단할 수 없는 명제인 ‘골드바흐의 추측’과 ‘연속체 가설’을 예로 들었다.

공리★ 시스템이 기본적으로 작동할 수 있도록 증명 없이 참으로 인정하는 명제.


인간만이 참거짓을 결정한다
골드바흐의 추측은 ‘2보다 큰 모든 짝수는 두 소수의 합으로 표현가능하다’인데, 18세기에 만들어졌지만 아직까지도 참이라고 할 수도, 거짓이라고 할 수도 없는 명제로 남아있다.

연속체 가설은 ‘자연수의 집합보다 크고 실수의 집합보다 작은 집합을 찾을 수 없다’는 것이다. 집합의 크기를 비교할 때 집합의 ‘기수’를 쓰는데, 자연수 집합의 기수보다 크고 실수의 기수보다 작은 기수를 갖는 집합이 있다는 수학자도 있고, 없다는 수학자도 있다. 만약 타당한 추론을 통해 그런 집합을 찾을 수 있거나 그런 집합은 없다는 것이 증명되면 연속체 가설은 콰인의 유형 중 참된 역설이나 거짓된 역설로 분류될 것이다.
 

김 교수는 “불완전성의 정리는 인공지능이 골드바흐의 추측이나 연속체 가설처럼 아직 참거짓이 결정되지 않은 명제를 해결할 수 없다는 사실을 보장한다”면서, “다만 인간이 참거짓을 결정한 문제는 인공지능도 인간을 흉내 내서 해결할 수 있을 것”이라고 말했다. 어떤 유형의 역설이든 인간이 해결하지 못한 역설을 인공지능이 앞서 해결할 수는 없다는 뜻이다. 역설적이게도, 인공지능을 두려워한 인간만이 모든 역설을 정복할 수 있는 유일한 존재다.