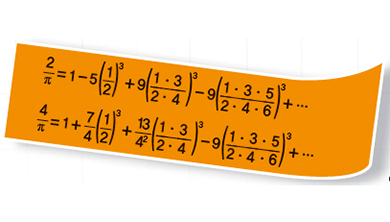d라이브러리 2017년 04호 수학동아

역설은 공통적으로 어딘가 앞뒤가 안 맞아 보인다. 그러나 우리가 느끼지 못한 사이에도 세상은 역설대로 작동한다. 투표 제도부터 게임 전략까지, 역설은 현실을 보여주는 힌트다.

다가오는 5월 9일, 제19대 대통령 선거가 열린다. 만 19세 이상인 모든 국민이 한 표씩 행사하고, 가장 많은 표를 얻은 후보 한 명이 대통령이 된다. 그런데 이런 단순한 최다득표제로는 국민의 선호도를 완벽하게 반영하지 못한다.

예를 들어, 세 후보 A, B, C가 출마한 선거에서 투표권을 가진 국민인 정혜인 씨, 이경환 씨, 박다솔 씨가 각 후보를 다음과 같은 순서로 선호한다고 가정해 보자.

《정혜인 씨는 후보 A를 가장 선호하고, 후보 C가 가장 별로라고 생각한다. 이경환 씨는 B, A, C 순서로 각 후보를 선호한다. 박다솔 씨의 후보 선호도는 순서대로 C, B, A다. 유권자 3명이 자신이 생각하는 최고의 후보에게 투표할 경우 당선자를 예측할 수 없다. 그러나 가장 많은 유권자가 만족할 후보는 이미 정해졌다. 과연 누굴까?》

인기 없는 후보가 당선되는 이유
유권자의 선호도를 바탕으로 후보가 둘씩 맞붙었을 때 누가 이길지 따져보면 후보 B는 A를 2번, C를 2번 이긴다. 후보 A는 B를 1번, C를 2번 이기고 후보 C는 A를 1번, B를 1번 이긴다. 이기는 경우에 승점을 1점씩 얻는다면 후보 B가 당선된다. 이 결과는 ‘누구만 아니라면, 후보 B도 괜찮다’는 유권자도 만족할 수 있다. 그러나 단순한 최다득표제에서는 후보 A나 C가 당선될 수도 있다. 다수결이 다수의 선호를 반영하지 못한다는 것이 바로 ‘투표의 역설’이다.

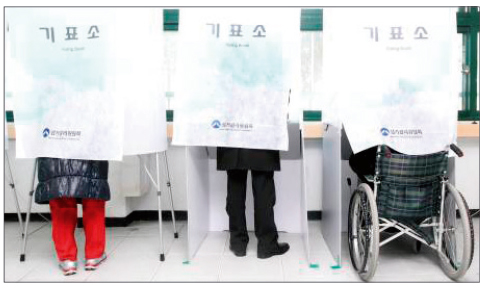
모든 유권자를 위한 완벽한 투표 제도는 없다.
모든 유권자가 선호도가 높은 순서대로 후보를 줄 세우는 제도는
오로지 특정 후보 한 명만 선호하는 유권자의 의견은 반영할 수 없다.

차가 막히면 도로를 없애라고?
십여 년 전까지만 해도 서울 도심에는 청계 고가 도로가 있었다. 이 도로는 신호등 없이 청계천 1가와 서울의 동쪽인 마장동을 연결했는데, 하루에만 자동차 12만 대가 몰려 극심한 교통 체증이 계속됐다.

2003년, 서울시는 청계천 복원 사업을 시작하면서 청계 고가 도로를 철거하기로 결정했다. 그러자 ‘도로를 없애면 지금보다 더 심한 교통 정체가 일어날 것’이라는 우려가 쏟아졌다.

2005년 10월, 청계 고가 도로가 있던 자리는 지금의 청계천으로 탈바꿈했다.

그러나 청계 고가 도로를 완전히 철거한 이후, 서울 도심의 교통 흐름은 오히려 철거 이전보다 원활해졌다. 도로를 없앴더니 오히려 교통 체증이 풀린다는 명제는 독일의 수학자 디트리히 브라에스의 이름을 딴 ‘브라에스의 역설’이다. 교통 체증을 해결하기 위해 도로를 추가하면 지름길로 가려는 운전자가 몰려들어 체증이 심해진다. 반면 도로의 수를 줄여서 어느 길로 가더라도 걸리는 시간은 비슷한 상태가 되면 도로망의 체증이 전체적으로 줄어든다.

혼자 살아도 죽고, 함께 살아도 죽는다면?
변형균류는 물에 떠다니거나 나무에 붙어 살면서 모습을 수시로 바꾸는 미생물이다. 이들은 혼자서 살면 나쁜 서식 환경에서 협력할 동료가 없어 결국 죽음에 이른다. 그렇다고 무리를 지어 살면 주변 환경에 적응하기는 쉽지만 심각한 먹이 경쟁으로 다 같이 죽을 수 있다. 그렇다면 변형균류가 살아남기 위해 선택한 전략은 무엇일까?

생명과학 전문 저널인 ‘이라이프’는 2017년 1월 13일에 변형균류의 역설적인 생존 방법에 관한 논문을 공개했다. 논문을 쓴 미국 예일대학교 학부생 종 쉬앤 탄과 캉 하오 청 싱가포르 공과대학 교수는 변형균류가 혼자서 살다가 무리지어 살고, 다시 혼자서 살기를 반복하면서 번성할 수 있었다고 밝혔다. 연구팀은 개체 수와 성장률 변수를 활용해 변형균류의 삶을 수학 모델로 만들었다. 그리고 삶의 형태를 계속 바꾸면 변형균류가 어떤 이익을 얻는지 분석했다.

변형균류는 혼자 살다가 환경이 나빠지면 협력 가능한 무리로 가서 원래 살던 서식지의 자원이 다시 회복될 때까지 버틴다. 그러다가 무리가 점점 커져 먹이 경쟁이 심각해지면 자원이 풍족한 서식지로 돌아와 혼자 생활한다.

변형균류의 삶은 생태계에서 발견한 ‘파론도의 역설’이라고 볼 수 있다. 스페인 물리학자 후안 파론도가 1996년에 발견한 이 역설은 ‘무한 번 시도했을 때 결국 패할 확률이 아주 높은 두 가지 게임을 교대로 하면 결국 게임에서 이길 수 있다’는 내용이다.

인생의 정답은 없다
컴퓨터가 사람의 생각과 습관을 파악하는 수준이 되면 이런 게임이 등장할지 모른다. 게임 서버에 접속하면 컴퓨터가 조종하는 캐릭터가 상자 A와 B를 보여준다. 상자 A는 투명해서 안에 든 게임머니 1억이 눈에 보인다. 반면 상자 B는 나무로 만들어져 안에 뭐가 들어있는지 모른다. 게임 참가자는 상자 A와 B를 둘 다 가질지, 상자 B만 가질지 결정해야 한다.

그런데 이 캐릭터는 참가자의 마음을 아주 잘 읽는다. 그래서 참가자가 상자 B만 갖기로 결심하는 즉시 상자 B에 게임머니 10억을 두고 사라진다. 반면 참가자가 상자 A와 B를 모두 갖기로 결심한다면 캐릭터는 상자 B에 쓸모없는 아이템만 두고 사라진다. 당신은 어떤 선택을 내릴 것인가?

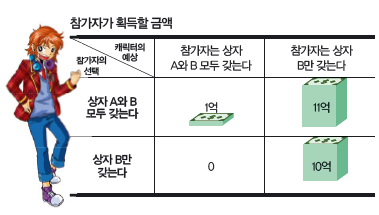
‘뉴컴의 역설’이라 불리는 이 문제에서 참가자의 선택은 갈린다. 어떤 사람은 상자 B만 갖기로 한다. 그러면 높은 확률로 10억을 가질 수 있다. 또 어떤 사람은 상자 A, B를 모두 갖기로 한다. 선택하는 시점에 상자 B의 내용물은 이미 정해져 있기 때문이다. 즉, 무엇이 들어 있든 적어도 상자 A에 든 1억을 더 가질 수 있다. 둘 중 어느 하나를 정답이라 할 수 없다. 이처럼 현실에서 마주하는 여러 문제도 뚜렷한 정답이 없는 경우가 대부분이다.

d라이브러리

Part 2. 현실을 비추는 거울, 역설