
만나서 반갑습니다. 전 ‘Mr. 착시’입니다. 본명은 신경 쓰지 마시고, 전 예술가니까 Mr. 착시라고 불러주세요. 착시를 일으키는 작품을 보면 눈이 즐겁지만 직접 만드는 건 어렵다고요? 착시는 수학적인 예술이에요. 보는 사람의 시선을 따라 조금만 계산하면 생생한 착시를 만들 수 있지요. <;수학동아>; 독자에게 특별히 몇 가지 노하우를 소개해 보겠습니다.

먼저 왼쪽 작품을 보세요. 이 작품은 벨기에의 화가 데이비드 맥도날드가 세상에 없는 불가능한 도형에서 영감을 얻어 만들었어요. 작품 속 삼각형은 영국의 수학자 로저 펜로즈 경의 이름을 딴 ‘펜로즈 삼각형’으로 유명하지만 이 삼각형을 최초로 만든 사람은 오스카 로이터스바르드라는 스웨덴의 그래픽 작가랍니다.
로이터스바르드는 어린 시절에 난독증 진단을 받아 사물의 크기와 거리를 정확하게 보기가 힘들었어요. 하지만 그런 장애를 딛고 1934년에 만든 불가능한 삼각형을 포함해서 살아있는 동안 2500가지나 되는 불가능한 도형을 만들었어요. 펜로즈 경은 로이터스바르드보다 늦었지만 독자적으로 불가능한 삼각형을 만들었다는군요.
마우리츠 에스허르와 같은 화가도 불가능한 도형에서 영감을 얻어 재미있는 작품을 그렸어요. 수직으로 떨어지는 폭포의 시작점과 끝점이 같은 평면에
있는 작품 ‘폭포’도 그 중 하나지요. 불가능한 도형은 화가뿐만 아니라 수학자, 심리학자에게도 재미난 연구 주제랍니다.
간단한 조작으로 불가능 도형 만들기
불가능한 도형을 만드는 방법을 알면 데이비드 맥도날드나 마우리츠 에스허르처럼 독특한 착시 그림을 그릴 수 있어요. 하지만 불가능한 도형은 실제로는 절대 만들 수 없어요. 실제로 만들려고 블록을 쌓다 보면 멀리 떨어진 두 블록을 무조건 연결해야만 하는 불가능한 상황이 나타나요. 독일 뮌헨에 있는 국립독일박물관의 펜로즈 삼각형 구조물도 특정한 각도에서 봐야만 삼각형으로 보여요. 즉, 불가능한 도형은 사실 모든 부분이 연결된 것처럼 보이게 그린 것일 뿐이지요.
2014년 브릿지스 컨퍼런스에서 당시 워털루대 소속이었던 티파니 잉글리스 박사는 블록으로 만든 평범한 입체도형을 불가능한 도형으로 바꾸는 방법을 발표했어요. 그 비결은 바로 멀리 떨어져 있는 블록과 가까이 있는 블록을 똑같은 크기로 그리는 거예요. 그러면 우리 눈은 블록 사이의 거리를 인식하지 못하고 두 블록이 마치 가까이 있는 것처럼 착각한답니다.
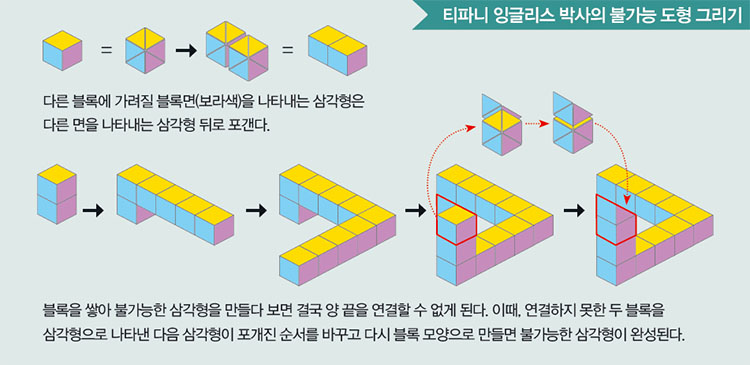
잉글리스 박사는 입체도형을 이루는 블록의 모든 면을 크기가 비슷한 삼각형으로 나타냈어요. 그 다음 블록을 쌓듯 삼각형을 차례차례 포개 블록의 구조를 표현했어요. 눈에 보이는 블록면을 나타내는 삼각형이 앞으로 나오게 포개면 돼요. 만약 블록끼리 붙어있지 않더라도 보는 방향에 따라 다른 블록에 가려진 블록이 있다면 이 부분 역시 삼각형을 포개 나타낼 수 있답니다.
블록을 삼각형으로 나타내는 방법을 이해했으면 이제 아쉽게 펜로즈 삼각형이 되지 못한 입체도형에서 포개진 삼각형을 찾아 포갠 순서를 바꿔 보세요. 이 과정은 다른 블록에 가려서 보이지 않던 면이 눈에 보이도록 블록 배치를 바꾼다는 뜻이에요.
어때요, 절대 연결할 수 없는 두 블록이 자연스럽게 연결된 것처럼 보이지요? 이런 방법으로 불가능한 도형을 다양하게 만들 수 있어요!

그림 속에 숨은 또 다른 그림
둥근 거울에 비추면 새로운 그림이 나타나는 기술도 있답니다. 바로 ‘애너모포시스’입니다. ‘왜상 화
법’이라고도 하지요. 그림을 쉽게 알아볼 수 없도록 늘리거나 찌그러트리는 이 기법은 특정한 위치
에서 보거나 거울과 같은 도구가 있어야만 제대로 볼 수 있어요.
거울 반사를 이용한 애너모포시스 이론을 가장 먼저 수학적으로 정리한 인물은 17세기 프랑스 파리의 수도사 장 프랑수아 니세롱이에요. 유명한 수학자였던 페르마, 데카르트, 카발리에리 등과 어울리며 최신 기하학과 광학을 익힌 니세롱은 1638년에 애너모포시스 이론을 정리한 최초의 책 <;신기한 원근법>;을 발표했어요.
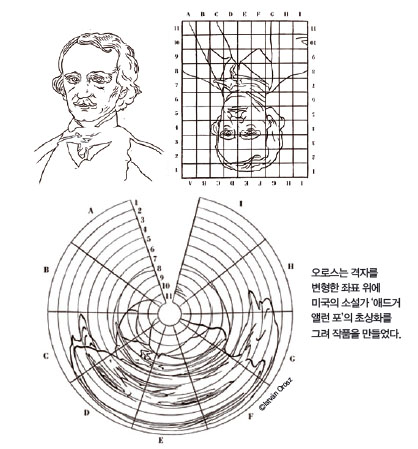
헝가리의 그래픽 디자이너 이스트반 오로스는 거울 반사를 이용한 왜상 화법의 대표 주자예요. 오로스에게 물어보니 작품을 만들 때 니세롱의 책을 참고한다더군요. 오로스의 그림은 거울에 비추기 전 상태라 해도 그 자체로 멋진 풍경화랍니다. 원기둥 거울에 비추기 전에는 어지러운 방 안의 모습인데 이 그림 한 가운데에 거울 기둥을 두니 거울 속에 아인슈타인이 나타났지요? 그렇게 어렵지 않는 수학으로 이런 작품을 만들 수 있다고 하니 착시 설계자로서 소개하지 않을 수 없지요!

거울 속에서만 제대로 볼 수 있다
오로스는 거울 중에서도 원기둥 거울이 있어야 제대로 볼 수 있는 작품을 주로 만들어요. 그림을 그리기에 앞서 바탕이 되는 격자를 원기둥 거울을 중심으로 부채꼴 모양이 되도록 길게 늘이지요. 그리고 그 격자 안에 그림을 그려요. 그러면 그림이 마치 부채꼴의 중심을 에워싼 것처럼 보인답니다. 격자 각각을 중심각이 몇 도인 부채꼴로 나타낼지는 격자의 개수로 계산할 수 있지요.
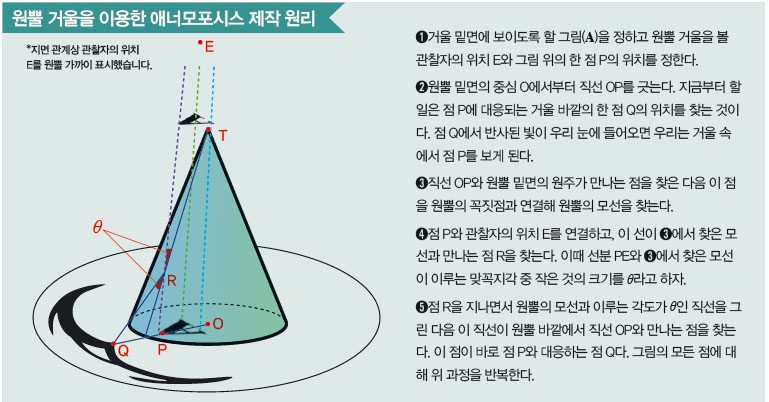
원뿔 거울을 가진 사람만 제대로 볼 수 있는 그림도 있어요. 이렇게 원뿔 거울 위에서 봐야만 하는 작품은 원기둥 거울보다 반사되기 전 그림이 훨씬 더 많이 찌그러져요. 제가 준비한 설명서를 따라하면 고리포터도 거울 반사를 이용한 애너모포시스와 한층 더 가까워질 거예요!

이번에는 또 다른 애너모포시스를 소개할게요. 거울을 쓰는 애너모포시스와 구분해 ‘기하학적 애너모포시스’라고 부르는 기법을 알려드리죠.
이 기법을 쓰면 작가가 의도한 특정한 위치에서만 숨어 있는 그림을 제대로 볼 수 있어요. 작가가 의도한 위치 밖에서는 진짜 그림이 보이지 않기 때문에 함부로 보여줄 수 없는 정보를 숨기는 수단으로도 쓰였답니다. 르네상스 시대에 활동한 독일의 화가 에르하르트 쇤은 자신과 정치적인 견해가 달랐던 황제 네 명의 초상화를 이 기법으로 그려서 감췄어요.
최근 이 기법을 적용한 작품을 쉽게 만날 수 있는 장소는 바로 트릭아트 미술관이에요. 트릭아트 미술관에 가면 마치 땅이 꺼지고 동물이 벽을 뚫고 나올 것만 같지요. 그건 작품이 그렇게 보이도록 작가가 계산한 위치를 따라 관람객이 이동하게 만들었기 때문이에요. 그런 위치를 일부러 감추려 했던 사람들과는 정 반대지요?

좌표가 변하면 트릭이 시작된다
넓은 도로나 벽을 캔버스로 삼아 그린 트릭아트 작품을 다른 위치에서 보면 어떻게 될까요? 네덜란드의 화가 레온 키어가 도로에 그린 작품 ‘레고 테라코타 군대’를 예로 들어 볼게요. 그림을 앞쪽에서 보면 진시황의 병마용을 재현한 레고 캐릭터가 생생하게 보입니다. 마치 땅을 파고 레고를 세워놓은 것 같아요.
하지만 그림을 뒤쪽에서 보면 줄맞춰 서 있던 작은 레고가 통나무처럼 길게 늘어난 것처럼 보이지요? 자세히 보면 그림이 제대로 보이는 지점을 중심으로 그림이 변형돼 있답니다.
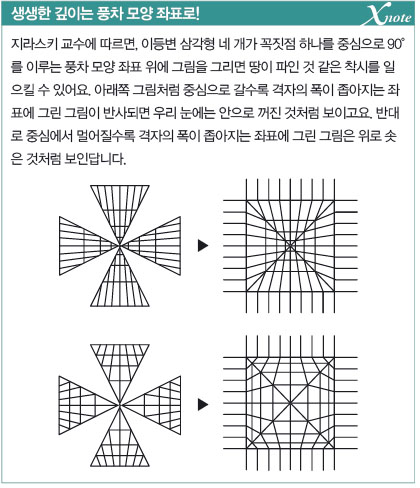
폴란드 크라쿠프공대 그래픽 공학과의 앤드류 지라스키 교수는 그림을 그릴 좌표의 생김새에 따라 착시 효과를 결정할 수 있다는 연구 결과를 발표했어요. 관람객은 누구나 자신이 서 있는 자리에서 보이는 대로 그림을 인식해요. 관람객의 시야를 가상의 벽이라고 가정하면, 그림에서 반사된 빛이 이 가상의 벽에 부딪혀서 만드는 상이 곧 관람객이 인식하는 그림이랍니다.
그래서 실제로는 사다리꼴 모양인 좌표 위에 그린 그림도 특정 위치에서 보면 마치 흔한 사각형 좌표 위에 그린 그림처럼 보이는 거지요. 이렇게 시야를 계산하면 의도한 그림이 잘 보이는 위치와 그렇지 않은 위치를 알 수 있어요. 많은 관객이 착시 그림을 가장 잘 볼 수 있도록 작품을 전시하는 것도 착시 설계자의 중요한 덕목이랍니다.




일본 메이지대 고등수학연구원 코키치 수기하라 교수는 2010년과 2013년에 각각 1위, 2015년에 2위를 했어요. 수기하라 교수의 작품은 종이와 풀, 가위만 있으면 쉽게 만들 수 있답니다. 고리포터도 저를 따라 만들어 보세요!
➊ 모호한 차고 지붕
차고 안에 노란 차가 서 있어요. 끝이 뾰족한 지붕은 특별할 것이 없고요. 그런데 거울을 보세요. 눈을 비비고 다시 봐도 차고의 지붕이 마치 산등성이처럼 울퉁불퉁하지요? 이게 어떻게 된 일일까요?
수기하라 교수는 특정 방향에서 본 지붕의 모서리가 마치 지붕에 수직인 평면으로 지붕을 잘랐을 때 나타나는 단면처럼 보이기 때문이라고 설명했어요. 지붕을 이루는 사각형 네 개 중 가운데 두 개는 사실 직사각형이 아닌 평행사변형이에요. 특정 방향에서만 지붕이 사진처럼 보일 뿐 실제로는 모서리가 들쭉날쭉하고 한 평면 위에 있지도 않아요. 종이비행기나 새 같기도 해요.
모호한 차고 지붕을 만드는 방법은 간단해요. 지붕과 지지대의 전개도를 오린 다음 실선과 점선을 따라 접고, 지지대를 지붕 밑에 붙여 형태를 고정하면 완성!

❷ 자석을 품은 미끄럼틀
이 미끄럼틀에는 어떤 착시현상이 숨어 있을까요? 맨 꼭대기에 빽빽하게 들어찬 공 여러 개가 아래로
굴러 떨어지지 않고 있어요. 놀랍게도 공을 미끄럼틀의 맨 끝에 두면 마치 자석에 끌리듯 위로 올라간답니다.
2010년 수상작인 이 미끄럼틀도 특정 방향에서만 평범한 미끄럼틀로 보이는 착시를 이용했어요. 다른 각도에서 보면 맨 꼭대기인줄 알았던 평평한 부분이 사실은 밑으로 움푹 들어가 있답니다. 그래서 공이 모두 이 부분으로 굴러가는 거랍니다.
이 작품도 미끄럼대와 미끄럼대를 받치는 지지대의 전개도를 오리고 붙여서 쉽게 만들 수 있어요. 실제로 각각 다른 각도로 기울어 있는 지지대가 모두 평행하게 보이는 위치를 찾아야만 신기한 미끄럼틀을 볼 수 있다는 점 잊지 마세요!


▼관련기사를 계속 보시려면?
INTRO. 당신의 눈을 속이는 착시 설계자
PART 1. 착시 설계자 따라잡기
PART 2. 아무도 몰랐던 착시의 비밀
사진 제공 및 도움 : 커트 베너, 데이비드 맥도날드, 이스트반 오로스, 레온키어, 코키치 수기하라, 파올로 디 라짜로
참고 문헌 : 티파니 잉글리스의 논문 ‘Constructing Drawings of Impossible Figures with xonometric Blocks and Pseudo-3D Manipulations’, 다니엘레 무라와 파올로 디 라짜로의 논문 ‘Figurative art, perception and hidden images in inverse perspective’, 안드레아스 니더의 논문 ‘Seeing more than meets the eye: processing of illusory contours in animals’, 이언 스튜어트의 책 <;생명의 수학>;











