d라이브러리

오는 10월 1일 파리에서 이스탄불로 가는 마술열차에 죽음의 마법을 걸었다.
- 에이스 -

설마 지난 몇 년 동안 벌어진 연쇄 살인 사건의 용의자 에이스?!
현장에 표식을 남긴 적은 있지만, 이렇게 사건을 미리 알린 적은 단 한 번도 없었다. 그렇다면 모방 범죄? 아니면 장난? 그런데 왜 내게 이런 초대장을 보낸 걸까?

마술 1 용의자의 위치를 찾아라!

마술열차에 오신 것을 환영합니다! 전 마술사 돈 가퍼필드입니다. 제 마술을 도와 주실 분이 필요한데요, 원하시는 분은 손을 들어 주세요. 아! 거기 첫 번째 줄에 안경 쓰신 남자 분, 나와 주세요.

이제 이 분은 어떤 사건의 용의자입니다. 저는 용의자를 검거해야 하는 형사죠. 여기 5장의 카드가 붙은 방 중 한 곳에 용의자가 숨을 겁니다. 숨으셨나요? 여러분도 용의자가 되어 마음속으로 한 곳을 정하세요.

사실 이곳에는 방이 총 9개 있습니다. 각 방마다 카드가 붙어 있죠. 방에는 동서남북 4곳에 문이 나 있어 다른 방으로 이동할 수 있습니다. 당연히 범인은 형사에게 잡히지 않기 위해 방과 방 사이를 이동합니다.

용의자, 3칸을 움직이세요. 용의자가 3칸을 움직였을 때쯤 형사가 어느 한 방으로 들어가 소리를 내면 용의자는 더 이상 움직일 수 없게 됩니다. 용의자는 어느 방향으로도 갈 수 있고, 머물렀던 곳으로 다시 돌아와도 상관없습니다. 다만, 무조건 3칸을 움직여야 합니다. 용의자, 이동하셨죠?
 
자, 이제 형사인 제가 촉을 바짝 세워 용의자의 위치를 추리해야겠군요. 아마도 용의자는 클로버 에이스(A)가 붙은 방에는 있지 않을 거예요. 따라서 저는 이 방을 폐쇄합니다.

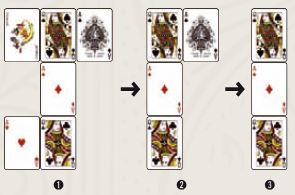
용의자 이번에도 3칸을 움직이세요. 흠…, 제 직감에 의하면 용의자는 다이아몬드 퀸(Q)과 하트 퀸, 이 두 곳에도 있지 않습니다. 따라서 폐쇄합니다.(➊)

이번엔 1칸을 움직이세요. 용의자가 이동하고 나면 하트 에이스와 조커가 붙은 방을 폐쇄할 겁니다.(➋) 이제 용의자가 갈 수 있는 방은 단 4곳입니다. 하하, 제가 용케도 빈 방만을 골라 폐쇄하고 있지요. 용의자 이제 2칸을 움직이세요. 전 스페이스 에이스 방을 폐쇄해야겠군요.(➌)

드디어 용의자를 잡을 시간이 다가왔습니다. 용의자는 이제 3칸을 움직이세요. 이동했죠? 그럼 제가 용의자의 위치를 파악해 방문을 열죠. 용의자는 바로, 다이아몬드 에이스에 있습니다!
 
범인 잡는 마술의 핵심은 홀짝성!

악! 하는 비명소리가 열차 전체를 뒤흔든다. 뒤늦게 방을 확인한 마술사는 너무 놀라 말조차 하지 못한다. 방 안에는 마술을 도와 준 남성이 싸늘한 시체가 되어 축 늘어져 있었기 때문이다. 이때 수학탐정 M에게 전화가 걸려온다.
“내 선물은 어땠소? 으하하~, 열차를 세우면 폭탄이 터질 것이오.”

당신 도대체! (전화가 끊어진다.) 역시 에이스인가? 사건 현장에 항상 에이스 카드를 남겨 두기 때문에 붙은 별명 에이스. 하지만 그의 모습을 본 사람은 단 한명도 없었다. 그는 언제나 한 치의 실수도 없이 사건 현장을 떠났다. 그렇다면 이번에도 계획적으로 다이아몬드 에이스 방에 시체를 갖다둔 것일까? 분명 에이스는 카드 마술의 트릭을 알고 있거나, 마술사와 한패! 우선 마술의 트릭을 밝혀 작은 단서라도 찾아야 해!

주어진 9장의 카드는 홀짝성을 갖는다. 홀짝성이란 두 집합 A, B가 어떤 시행을 했을 때 홀수, 짝수와 같이 항상 상반되는 두 가지 그룹으로 나뉘는 것을 말한다. 예를 들어 정수와 홀수의 집합이 있을 때 덧셈(시행)을 하면 정수가 홀수일 때는 짝수가 되고, 정수가 짝수일 때는 홀수가 된다. 이런 홀짝성은 그래프 이론이나 이산수학의 문제를 풀 때 많이 활용된다.

돈 가퍼필드의 카드 마술에서는 홀짝성을 이용해 9개의 방을 두 집합으로 나눌 수 있다. 편리하게 ○, ×라고 하자. 그러면 신기하게도 용의자가 ○에 숨었을 때 홀수 번 움직이면 무조건 ×자리에, 짝수 번 움직이면 ○자리에 가게 된다.
 
➊에서 3번 움직였을 때 갈 수 있는 경로
➊→➋→➌→➏, ➊→➋→➌→➋, ➊→➋→➊→➋, ➊→➋→➎→➑,
➊→➋→➎→➏, ➊→➋→➎→➋, ➊→➋→➎→➍, ➊→➍→➐→➑,
➊→➍→➐→➍, ➊→➍→➊→➍, ➊→➍→➎→➋, ➊→➍→➎→➍,
➊→➍→➎→➏, ➊→➍→➎→➑

예를 들어 범인이 처음에 조커 자리(➊)에 숨었다고 가정하자. 3번 움직여서 갈 수 있는 경우는 총 14가지다. 최종 도착지는 ➋, ➍, ➏, ➑ 중 하나로, 모두 ×집합에 속한다. 반대로 용의자가 ×에 숨었을 때 홀수 번 움직이면 무조건 ○자리에, 짝수 번 움직이면 ×자리에 위치한다.

눈치빠른 사람들은 알겠지만 돈 가퍼필드는 처음에 5개의 방만 공개하며, 용의자가 무조건 ○자리에 숨도록 했다. 따라서 이후부터는 마술사가 마음대로 용의자의 위치를 정할 수 있다. 즉 자기가 말한 숫자가 홀수인지, 짝수인지에 따라 용의자가 어느 곳에 있는지 파악하고 한 곳 또는 두 곳씩 방을 폐쇄하면 된다. 주의할 점은 마지막에 남은 방이 연달아 있는 세 칸이어야 한다는 것이다. 그리고 이때 ○, ×, ○방이 남았다면 ×에 위치하도록, ×, ○, ×방이 남았다면 ○에 위치하도록 숫자를 말해야 한다.

마술을 할 때 긴장감을 살리려면 방을 폐쇄할 때마다 고민을 하는 모습을 보이고, 틀린 답을 말했다가 재빨리 수정하는 방법을 사용해도 좋다.

이번 마술의 비밀은 홀짝성! 처음부터 끝까지 마술사가 용의자의 위치를 조종할 수 있지. 범인이 이 사실을 안다고 해도, 마술사가 폐쇄하는 방에 따라서 용의자의 최종 위치는 달라진다. 따라서 살인 사건은 마술사가 마지막 방을 폐쇄하고 방을 공개할 때까지 약 3분 동안 벌어진 셈이다.
그런데 건장한 남자를 그 짧은 시간에 살해했다는 건 말이 안 돼. 결국 범인은 마술사와 한패라는 건가! 마술사의 협조 없이는 사건이 일어날 수 없다고.
조 형사, 지금 그 마술사 어디에 있지? 뭐? 시체가 사라졌다고? 그리고 그 시체는 에이스가 1년 전 살해한 사람의 동생이라고?!

마술 2 상대방이 고른 카드를 알아맞혀라!

시체는 감쪽같이 사라졌고, 살인범은 아직 열차 안에 있다. 수학탐정 M은 돈 가퍼필드를 취조하고 있고, 형사들은 폭탄의 행방을 찾고 있다. 형사들의 취조 결과 용의선상에서 벗어난 마술사들과 승객들은 정해진 객실에 머무르고 있다. 마술사들은 승객들을 안정시키기 위해 각자 자신의 대표 마술을 선보이는데….

카드 알아맞히기 마술을 선보일 마술사 엘리스입니다. 열차 안이 조금 뒤숭숭하지만, 이런 위기를 환상적인 마술로 극복하자고요! 제게는 15장의 카드가 있습니다. 손님, 카드를 섞어 주시겠습니까?

손님께서 섞으신 카드를 순서대로 5행 3열로 놓겠습니다. 15장의 카드 중에서 한 장을 고르세요. 제가 알면 안 되니까 말은 하지 마시고요. 고르신 카드가 어느 열에 있는 지만 알려 주세요.
“3열이요.”

카드를 하나로 모은 뒤 다시 5행 3열로 늘어놓는다.

제가 카드를 뒤죽박죽으로 섞어 봤습니다. 이번엔 손님께서 고른 카드가 몇 열에 있나요?
“1열에 있어요.”

다시 카드를 하나로 모은 뒤, 5행 3열로 늘어놓는다.

마지막으로 손님께서 고른 카드는 어느 열에 있나요?
“2열이요.”
손님이 고르신 카드는…. 바로 다이아몬드 에이스입니다!
“어…, 어떻게 알았죠?”

이때 수학탐정 M에게 다시 전화가 걸려 온다.
“두 번째 선물을 준비했소. 마술사 엘리스에게서 힌트를 얻으시오.”
수학탐정은 급하게 엘리스를 찾는다. 엘리스는 카드 알아맞히기 마술을 하고 있었을 뿐 자신은 아무것도 모른다고 말하는데….

카드 알아맞히기 마술의 비밀은 행렬!

카드 알아맞히는 마술의 비밀은 상대방이 말한 열의 위치를 바탕으로, 그 카드가 3행에 오도록 행렬의 위치를 바꾸는 것이다. 행렬이란, 행과 열에 수를 배열하여 직사각형을 이루는 수의 집합이다. 행은 가로 줄, 열은 세로 줄을 의미한다. 11은 1행 1열, 21은 2행 1열을 뜻한다. 마술에 쓰인 방법은 다음과 같다.
 
카드 위치 바꾸기

❶ 15장의 카드를 5행 3열로 놓은 뒤 5×3 행렬로 표시한다.
❷ 상대방이 열의 위치를 말하면, 그 열이 가운데 오도록 카드를 모은다. 여기서는 3열이라고 했으므로, 1열, 3열, 2열 순으로 카드를 모은다.
카드를 모을 때는 아래에서 위로, 즉 51, 41, 31, 21, 11순으로 카드를 걷어들여 11이 위에 오도록 걷는다. 그러면 15장의 카드를 다 모았을 때, 12, 즉 클로버 잭 카드가 맨 위에 놓인다.
❸ 15장의 카드를 순서대로 놓는다. 이때 행을 먼저 채운다. 그러면 1행 1열에는 12(클로버 잭)가, 5행 3열에는 51(다이아몬드 잭)이 위치한다.

카드를 이렇게 놓는 이유는 상대방이 고른 카드가 3행에 오도록 하기 위해서다. 3열의 카드가 총 5장 있으므로 한 번 자리를 바꿔서는 2행과 3행, 4행까지 카드가 걸쳐 있게 된다. 따라서 같은 방법으로 한 번 더 자리를 바꿔야 한다.

즉 상대방에게 다시 열의 위치를 묻고, 카드를 모았다가 나열한다. 이번에는 1열이라고 대답했으므로 2열, 1열, 3열 순으로 카드를 아래서 위로 모으고 행부터 채워 5행 3열로 늘어놓는다. 그러면 32(스페이스 킹)가 1행 1열에, 41(스페이스 잭)이 5행 3열에 놓인다. 답이 될 수 있는 후보는 맨처음 3열에 있던 (13, 23, 33, 43, 53) 중 카드의 위치가 바뀐 뒤 1열로 옮겨진 (23, 53)이다. 마지막으로 열의 위치를 물었을 때 2열이라고 했으므로 정답은 23, 다이아몬드 에이스다.

카드 알아맞히기의 트릭은 상대방이 고른 카드를 3행에 위치하도록 만드는 것! 그렇다면 숫자 3과 무슨 관련이 있는 건 아닐까? 조 형사, 재빨리 3호차로 가 보지. 앗! 또다른 시체다!

카드 마술의 핵심은 불변량!

마술열차 안에서만 벌써 두 사람이 죽었지만, 범인의 행방은 전혀 알 수가 없다. 돈 가퍼필드를 포함해 열차 안에 있는 모든 사람이 알리바이가 있는 상황이다. 아무리 찾아도 나오지 않는 폭탄은 열차에 없다고 판단하고, 더 이상의 희생자를 막기 위해 가까운 역에 열차를 세우기로 한다. 무언가 단서를 놓치고 있다고 생각한 수학탐정 M은 유일한 단서인 카드를 섞으며 범인의 행적을 따지고 있다.

어? 방금 내가 카드를 섞지 않았나? 어째서 카드의 순서가 같은 거지? 현재 스페이스 에이스 세 장 뒤에 하트 퀸이 있다. 다시 한 번 리플 셔틀을 해 보아도, 어라? 이번에도 마찬가지네. 리플 셔틀은 반으로 나눈 카드를 좌르륵 소리를 내며 양손에서 번갈아가며 한 장씩 떨어지도록 하는 기술. 이 리플 셔틀이 혹시 *불변량이란 말인가?!

n개의 카드가 차곡차곡 쌓여 있다고 가정하자. 위에서부터 셌을 때 두 장의 카드가 a와 b의 위치에 있다면 둘의 관계를 b-a로 나타낼 수 있다. 그런데 카드 한 더미에서 일부분을 떼어낸 뒤, 맨 밑에 있는 카드 아래에 놓아도 카드의 순서는 바뀌지 않는다.

예를 들어 10장의 카드가 있을 때, 하트 에이스와 클로버 잭이 위에서부터 각각 2번째와 5번째 위치한다고 하자. 그러면 차이는 3이다. 두 번째 위치에서 카드를 떼어 맨 아래 놓으면, 하트 에이스의 위치는 10이고 잭은 위치는 3으로 옮겨간다. 즉 차이는 3-10=-7이지만 카드 더미는 맨 밑에서 맨 위로 연결되기 때문에 -7은 3과 같다. 차례대로 카드가 섞이는 리플 셔틀도 마찬가지 성질을 갖는다.

카드를 떼어낸 뒤, 뒤에 붙이거나 리플 셔틀을 하면 카드의 순서는 바뀌지 않지만 사람들은 카드를 섞고 있다고 생각한다. 따라서 마술사들이 트릭으로 많이 사용한다.

앗! 그러고 보니 에이스는 한 번도 경고 살인을 한 적이 없었어. 범인은 에이스가 아니야! 에이스가 범인이라고 여기게 하고 싶은 또 다른 자라구! 그래서 다이아몬드 에이스를 사건과 계속 관련시켰던 거야. 그렇다면 범인은? 사라진 시체! 시체가 범인이었기 때문에 단서를 찾을 수 없었던 거야. 범인이 시체인 척한 거라구! 그럼 두 번째 시체가 진짜 에이스?!

우후훗, 나는 이번 부다페스트역에서 내린다. 난 내 형을 죽인 에이스를 용서할 수 없었어! 하지만 경찰은 에이스의 존재조차 밝히지 못했지. 흐흐흐…. 수학탐정 M, 넌 결코 날 찾을 수 없을 거야!

*불변량 : 방금 일어난 일에 상관없이 원래의 값을 유지하는 성질을 말한다.