d라이브러리

우리는 각을 재고 싶을 때, 각도기를 이용한다. 각도기에는 0°부터 360°까지 표시되어 있어 편리하게 각의 크기를 잴 수 있기 때문이다. 그런데 언제부터 각의 크기를 1°, 2°와 같이 쟀을까? 그리고 왜 한 바퀴를 완전히 회전한 각의 크기는 100°나 200°가 아니라 360°라고 정했을까? 그 이유를 알려면 인류가 처음 각의 크기를 생각한 고대 바빌로니아로 거슬러 가야 한다.

위치를 나타내는 거리와 각도

흔히 거리를 말할 때는 미터, 킬로미터 등의 단위를 쓰고, 방향을 말할 때는 동서남북을 이용한다. 학교가 집으로부터 동쪽으로 3km의 거리에 있다고 하면 집을 기준으로 해서 학교가 어디쯤 있는지 쉽게 짐작할 수 있다. 그러나 동서남북 방향을 알기 어려운 곳에서는 위치를 표현하기 위해 시계를 이용하기도 한다. 가령 공원이 2시방향에 있다고 하면 정면에서 약간 오른쪽에 있다는 뜻이다. 그리고 우리는 시계 눈금 한 칸이 30°임을 알기 때문에 2시 방향은 대략 오른쪽으로 60°정도라는 것을 알 수 있다. 이것을 좀 더 정확히 표현하면 진행 방향으로 뻗은 선과 지금 위치와 공원을 이은 선이 이루는 각이 60°라는 것이다.
 

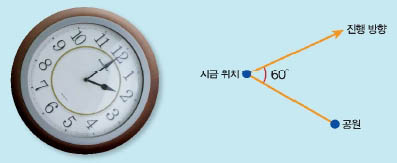
그런데 시계에서 한 시간 동안 움직인 각이 30°라는 것은 무엇을 의미할까? 시계의 중심에서 이웃하는 두 숫자에 선을 그었을 때, 그 선이 이루는 각이 30°도라는 것인데 그 이유는 한 바퀴를 360°로 정했기 때문이다. 360이라는 기준은 아주 오래 전에 고대 바빌로니아에서 정해졌다. 기원전 사용했던 각의 단위를 지금까지 쓰고 있다니 매우 놀랍고 신기한 일이다.

왜 360° 일까?

아주 오래 전부터 사람들은 1년을 주기로 계절과 날씨가 반복된다는 것을 깨달았다. 사람들은 농사를 지으면서 정착생활을 시작했고, 따라서 때를 정확히 아는 것은 매우 중요한 일이었다. 1년의 길이를 알기 위해 그림자의 길이가 똑같아질 때까지의 날을 세기도 하고, 별이 똑같은 자리에 올 때까지의 날을 세기도 했다. 이렇게 1년의 날을 정한 뒤 12달로 나누어 달력을 만들면서 천문학과 역법이 발달했다. 나라마다 1년의 길이가 조금씩 달랐는데 페르시아는 1년을 360일로, 이집트는 365일로 달력을 만들었다. 그 당시 정확한 달은 권력을 의미했기 때문에 대부분의 나라는 1년이 365일 정도라는 것을 알고 있었다.

이처럼 고대인에게 별이 제자리로 돌아오는 데 걸리는 약 360일이란 숫자가 매우 중요했기 때문에, 한 바퀴 도는 각도를 360°로 생각한 것은 자연스러운 일이다. 즉 1년에 한 바퀴 도는 항성이 하루에 움직이는 각도를 1°로 결정한 것이다.

한편, 고대 바빌로니아에서는 원의 반지름으로 원주를 차례차례 잘라 나가면 여섯번 만에 제자리로 돌아온다는 사실을 알고 있었다. 더구나 360을 6으로 나누면 그들이 사용했던 육십진법의 기본수 60이 된다.

고대 기하학의 발달
 

한편, 오늘날에도 그렇듯이 고대 학자들도 문명이 앞선 나라에 가서 선진문물을 배우곤 했다. 기하학의 창시자라고 하는 탈레스는 이집트를 여행하면서 그리스보다 먼저 발달한 기하학을 접했다. 이집트에서는 기하학을 이용해 농지 경계를 정하고, 피라미드와 같이 거대한 건축물을 만드는 실용적인 수학이 발달해 있었다. 그러나 여행을 마친 탈레스는 기하학을 이론적인 수학으로 정리했다. 바빌로니아와 이집트에서는 생활에서 필요한 각의 크기를 재고 계산하는 데 쓰였다면 탈레스는 각의 성질을 증명하는 데 초점을 둔 것이다. 탈레스는 두 직선이 만날 때 맞꼭지각이 같다는 것과 이등변삼각형에서 두 밑각의 크기가 같다는 것을 증명했다.

각을 재는 또 다른 단위, 호도법

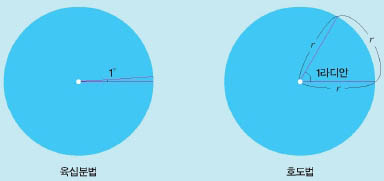
육십분법에서 1°는 원주(원의 둘레)를 360등분한 각 호에 대한 중심각으로 정했다. 그런데 근대에 와서 자연과학과 공학이 발달하면서 새로운 각의 단위가 필요했다. 1714년에 로저 코테스가 만든 ‘호도법’은 호를 이용해서 각을 측정하는 방법으로 그 단위는 ‘라디안’이다. 호도법에서 1라디안은 반지름과 호의 길이가 같을 때의 각의 크기로 정한다. 1라디안의 값을 알기 위해 부채꼴과 원의 각과 호의 길이로 비례식을 세우면 다음과 같다.

1라디안 : r = 360° : 2πr
(부채꼴의 중심각) (호의 길이) (중심각) (원주)
 

그런데 360°가 한 바퀴를 회전한 각도를 의미한다면 2회전이나 3회전은 어떻게 나타낼 수 있을까? 이런 문제를 해결하기 위해 각의 뜻이 더 확장되었다. 각은 360°에서 끝나는 것이 아니라 두 바퀴를 돌면 720°, 세 바퀴를 돌면 1080°로 말할 수 있다. 또 방향이 반대일 때는 음의 부호를 이용해서 표현할 수 있다. 예를 들면, -180°는 반대방향으로 180°를 의미한다.

우리가 쓰고 있는 각의 단위인 육십분법이 고대 바빌로니아인들의 발견부터 시작되었다니 고대인의 지혜에 감탄을 금할 수 없다. 그러나 각의 단위에는 육십분법뿐 아니라 자연과학과 공학에 쓰이는 호도법도 있으니 어떤 단위를 사용하든 그 단위가 무엇인지 확실히 알고 사용해야 한다.