d라이브러리

코앞으로 다가온 크리스마스에 오일러와 학생들은 크리스마스트리를 장식하기로 했다. 수학을 사랑하는 오일러답게 트리 장식품도 수와 기호 등 온통 수학이다. 그런데 수 장식을 보며 하나 학생이 재밌는 문제를 떠올렸다. 일명 ‘경로의 최대 합 문제’다.

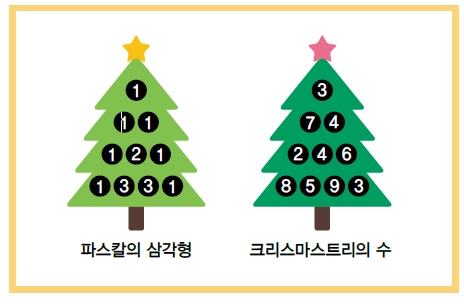
트리를 장식하던 하나는 수들이 마치 ‘파스칼의 삼각형’ 모양으로 나열된 것을 발견했다. 파스칼의 삼각형은 이름처럼 수를 삼각형 모양으로 배열해 놓은 것이다. 1을 시작으로 아랫줄로 내려가면서 수의 개수를 하나씩 늘려 삼각형 모양으로 수를 나열한다. 이때 양 끝에는 항상 1이 오며, 윗줄의 두 수를 더한 값을 바로 아랫줄에 적는다.

트리의 수들은 파스칼의 삼각형처럼 일정한 규칙을 갖진 않지만, 모두 한 자릿수로 삼각형 모양을
이루고 있다. 이윽고 하나는 삼각형의 꼭대기에서 시작해 인접한 수를 따라 내려갈 때, 지나는 수들의 합이 가장 큰 경로는 무엇일지 궁금해졌다. 한 걸음 더 나아가 한 자릿수들이 무작위로 삼각형 모양으로 나열돼 있을 때 항상 최댓값을 가지는 경로를 찾는 방법을 알고 싶어졌다.

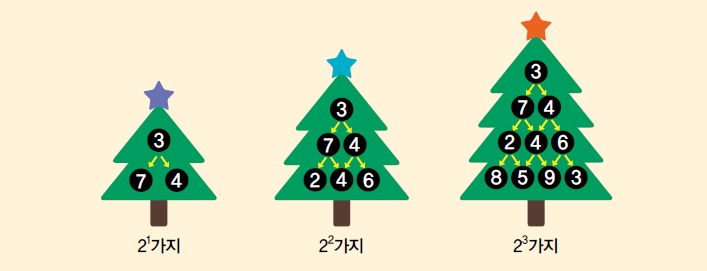
200억 년을 1분 이내로 줄이는 방법

수를 읽기 힘들 정도로 많은 가짓수에 놀란 학생들에게 오일러는 좀 더 효율적으로 계산하는 방
법을 소개했다. 중간 합을 구하는 방법이다.

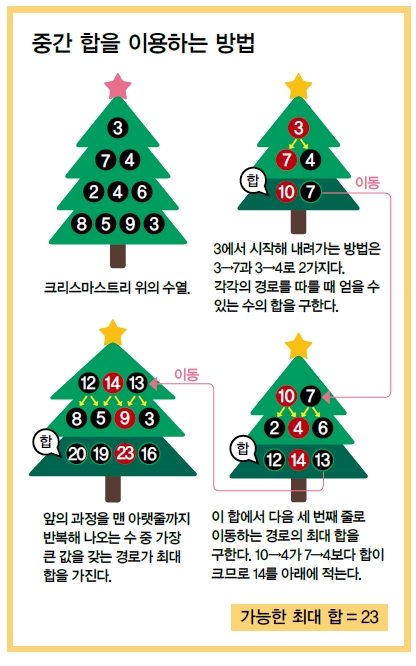
두 번째는 맨 아래에서 위로 이동하면서 경로를 찾는 방법이다. 트리의 세 번째 줄부터 시작해보자. 2에서 아래로 내려가는 경우는 8 또는 5다. 이때 5보다 8이 더 크므로 2→5로 가는 경로를 없앤다. 이 방식으로 세 번째 줄에서 네 번째 줄로 가는 가능한 경로를 정리하면 아래와 같다.

세 번째 줄의 수들을 앞서 고른 경로에 따른 중간 합으로 대체한다. 그리고 바로 윗줄에서 내려오는 경로 중 높은 합의 경로만 남기고 나머지를 지운다. 이 과정을 반복하면 3+20=23이 최대 합이라는 걸 알 수 있다.

이 두 가지 해결 방법은 100줄의 삼각형 수열에서 최대 합을 가지는 경로를 찾는 오일러 프로젝트 67번 문제에 적용할 수 있다. 꼭대기에서 바닥에 이르는 경로의 합 중 최댓값은 얼마일지, 코딩을 이용해 구해보자.

●오일러 프로젝트 67번 문제를 해결하려면?

100줄인 삼각형의 꼭대기부터 맨 아래까지 내려가는 경우의 수는 정말 많아서, 아무리 컴퓨터라고 해도 하나하나 계산하는 것은 무리예요. 이렇게 무작정 계산하는 것을 코딩에서는 ‘Brute-force 방법’이라고 부르는데, 우리말로 하면 ‘우격다짐’ 정도 됩니다. 계산할 양이 적다면 쓸 수 있지만, 규모가 커지면 통하지 않아 머리를 써야 하지요. 그래서 이번 문제에는 본문에 나왔던 두 가지 방법을 써야 해요.

하지만 이 방법을 쓸 때도 특별한 전략이 필요해요. 예시로 나왔던 삼각형 수열의 꼭대기에서 셋째 줄까지 이동하는 네 가지의 경로를 살펴볼까요?

3+7+2, 3+7+4, 3+4+4, 3+4+6

가만히 보면 3+7이나 3+4 같은 계산이 반복되는 걸 알 수 있지요. 그러니 이런 중간 합들을 어딘가에 기록해 둔다면 계산이 훨씬 빨라지겠죠? 이 방식을 이용해 삼각형을 구성하는 수 데이터는 줄별로 T라는 목록에 담겨 있다고 하고 코드를 만들어볼게요.

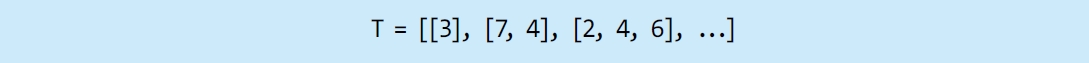
주의해야 할 점이 컴퓨터에서는 0이 첫 번째고, 그다음 1이 두 번째를 뜻해요. 그래서 T 목록에서 위에서 2번째 줄, 1번째 숫자 ‘7’은 (1, 0)이어서 T[1][0]으로 나타낼 수 있어요. 이제 위부터 x번째 줄, y번째에 있는 (x, y)의 중간 합은, (x-1, y-1)의 값과 (x-1, y)의 값을 현재의 (x, y) 값에다가 더하는 것과 같아요. 다만 이때 왼쪽 가장자리나 오른쪽 가장자리에서 리스트의 첨자가 범위를 벗어나지 않게 하려고 max(0, y-1)이나 min(x-1, y) 같은 식으로 보호해요. 이런점을 생각한 다음에 한번 스스로 코드를 만들어보고, 정답은 수학동아 블로그(mathdonga.blog.me)에서 확인해보세요!