d라이브러리

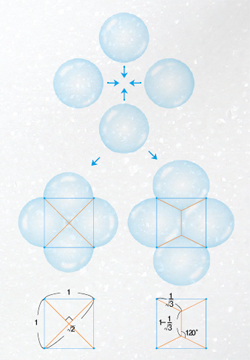
비눗방울이 여럿 모인 것이 비누거품이다. 비눗방울은 겉넓이를 최소화하려는 성질 때문에 동그랗다. 그러나 비눗방울이 동그래야 한다는 사실은 1950년대에 와서야 수학적으로 증명됐다. 비눗방울이 하나 있을 때는 동그란 곡면만 있지만 비눗방울이 여럿 모인 비누거품에서는 곡면이 3개 모이는 곡선이 생겨난다. 방울 4개가 만나더라도 곡면 4개가 모이는 곡선은 생기지 않는다. 왜 그럴까.

정사각형의 꼭짓점에 있는 점 4개를 생각해 보자. 이들 점을 잇는 가장 짧은 선분은 무엇일까. 얼핏 생각해 보면 서로 대각선에 위치한 점들을 잇는 직선 2개일 것 같다. 한 변의 길이가 1이라면 ‘X’자 형태로 점들을 잇는 선분 길이의 합은 2 2이고 두 선분 사이의 각도는 90°다. 그러나 점 4개를 잇는 가장 짧은 경로는 두 지점에서 선분 3개가 서로 120°의 각도로 만나는 형태다. 길이를 계산해 보면 ‘1+ 3 ’(≒2.732)으로 2 2(≒2.828)보다 짧다.

최소의 밀랍으로 최대의 집을 만들려면

겉넓이를 최소화하려는 비누거품은 결국 길이를 최소로 만들기 때문에 비누거품의 세곡면은 곡선을 따라서 120°의 각도를 이루게 된다. 두 유리 사이에 끼인 비누거품을 보면 120° 구조를 갖고 있고, 이를 건축에 응용한 베이징 올림픽 수영장 ‘워터큐브’의 거품구조는 유명하다. 벌집도 대표적인 120° 구조인데, 이는 최소의 밀랍으로 최대의 집을 만들어야 하기 때문이다. 현무암 표면에서도 이런 패턴을 볼 수 있다. 용암이 굳으며 수축할 때 120°로 쪼개져야 쪼개진 면을 최소화하면서 안정해질 수 있기 때문이다.

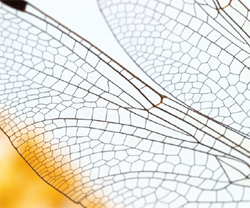
한편 비누거품이 철사처럼 견고한 구조와 만날 때는 90°를 이룬다. 이 경우 90°로 만나야 곡면의 넓이, 곡선의 길이가 최소가 되기 때문이다. 이런 패턴은 생물체에서도 만날 수 있다. 예를 들어 잠자리 날개를 보면 얇은 줄(날개맥)끼리는 120°를 이루지만 굵은
줄과 얇은 줄이 만날 때는 90°를 이룬다.

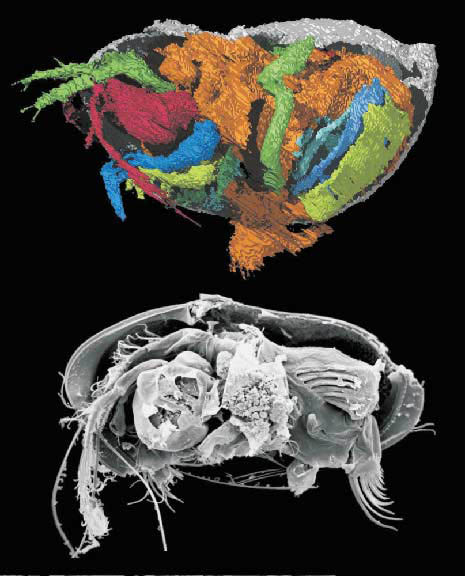
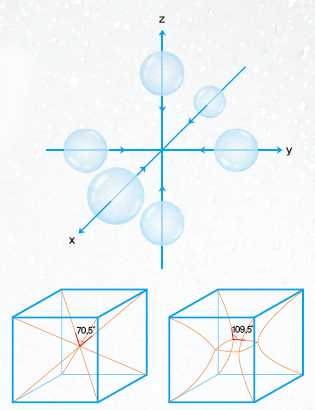
비누거품을 자세히 관찰해 보면 곡면 3개가 120°의 각도로 한 곡선을 따라 서로 모이고, 다시 이런 곡선 4개는 서로 일정한 각도로 한 점에서 모인다. 이들 곡선 4개 중 2개씩 이루는 각도는 모두가 109.5°다. 이는 정사면체의 중심에서 네 꼭짓점으로 잇는 선분들이 이루는 각도다. 독일의 생물학자 에른스트 헤켈이 스케치한 원생동물 방산충의 뼈대를 보면 중심의 방울만 없다면 정사면체에서 중심과 모서리를 잇는 평면들로 이뤄졌음을 알 수 있다.

여기서 우리는 곡면끼리 120°로, 곡선끼리 109.5°로 만나고 있다는 사실을 관찰할 수 있다. 살아 있는 방산충은 원형질의 거품이 많이 있는데, 그 속의 고형물질은 거품의 구석진 곳에 쌓이게 된다. 방산충이 죽은 뒤에는 이 고형 물질만 뼈대로 남아 방산충의 거품구조를 생생하게 보여준다.

우리가 일상생활에서 보는 다양한 거품에는 이 두 각도 120°와 109.5°가 항상 나타난다. 심지어 폭이 수십억 광년이 되는 우주의 3차원 지도를 보면 은하들이 모여 있는 모습도 거대한 거품 구조를 이루고 있음을 알 수 있다. 즉 은하가 우주 공간에 골고루 퍼져 있는 게 아니라 거품 막에 해당하는 부분에 주로 있고 거품 안은 텅 비어 있다.




철 망 을 비 눗 물 에 담 글 때

그러면 비누거품에서는 120°와 109.5° 이외의 다른 각도는 볼 수 없을까. 120°와 109.5°는 각각 정삼각형과 정사면체의 중심에서 생기는 각도이므로, 비누거품에 다른 각도가 생긴다면 그 가능성이 가장 큰 것은 정육면체에서 생기는 각도일 것이다. 즉 정육면체의 중심에서 각 꼭짓점으로 잇는 8개의 선분들이 이루는 각도인 70.5°일 가능성이다.

그러나 실제로 정육면체의 모서리 형태로 만든 철사를 비눗물에 담갔다가 꺼내면 다른 형태의 거품 막이 나타난다. 그 이유는 이 비누거품 막의 넓이가 정육면체에서 8개의 선
분들이 이루는 평면의 넓이보다 작기 때문이다. 그래서 비누거품에서는 70.5°의 각도가 생기지 않는다.이처럼 다른 각도가 비누거품에서 생기지 않음을 보이기 위해서는 먼저 구면에서 120°로 만나는 철망을 만들어야 한다. 이런 철망을 만들 수 있는 가짓수는 9가지가 있다. 이 철망으로 비누거품을 만들어 보면 구면의 중심으로부터 철망에 이르는 선분들의 집합(즉 중심과 철망을 지나는 부채꼴들의 집합)과 일치하는 경우는 2가지밖에 없다. 그래서 이 2가지에서 생기는 각도 120°와 109.5° 이외의 각도는 비누거품에 나타나지 않는다. 이에 대한 수학적인 증명은 1976년에야 완성됐다.



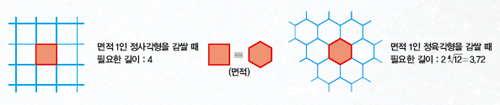
비누거품 구조는 평면과 공간의 분할 문제와 밀접하게 관련돼 있다. 평면을 효율적으로 분할하는 방법은 정사각형 구조가 아니고 벌집과 같은 정육각형 구조다. 여기서 한 구조가 평면을 효율적으로 분할한다는 말은 분할되는 영역들의 넓이가 모두 같을 때 단위
넓이당 그 구조의 둘레가 가장 짧다는 뜻이다. 길이가 최소가 되려면 90°의 사각형이 아니라 120°의 육각형이어야 하고, 가장 효율적으로 평면을 나누려면 변의 길이가 같은 정육각형이어야 하기 때문이다.

벌 은 뛰 어 난 수 학 자



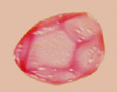
한편 양면, 즉 두 층으로 된 벌집에서는 두 면의 벌집이 서로 만나는 중간 부분에서 효율적으로 공간을 분할해야 하는 문제가 생긴다. 벌들은 마름모 3개를 이용해 두 방을 나눴다. 그런데 1964년에 한 수학자는 벌집보다 0.1% 작은 넓이의 구획방법을 발견했다. 그러나 이미 수억 년 전에 계산기 없이 이런 것을 발견한 벌들에 비해 인간의 업적은 미미해 보인다.

그러면 3차원 공간을 가장 효율적으로 분할하는 방법은 무엇인가. 벽돌과 같은 정육면체인가. 아니면 마름모로 이뤄진 12면체인가. 아니면 정사각형 6개와 정육각형 8개로 된 14면체인가. 정육면체는 각도가 90°여서 효율적 분할이 될 수 없고, 12면체와 14면체는 모서리 각도가 120°이지만 꼭짓점에서 생기는 각도는 109.5°가 아니어서 이 역시 효율적 분할이 아니다.









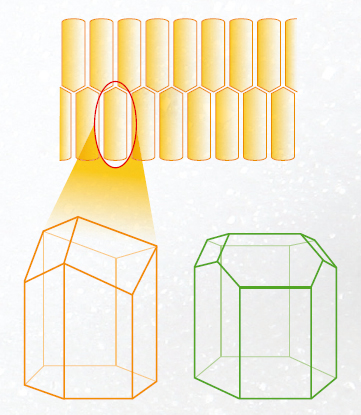
흥미롭게도 해답은 식물에서 찾을 수 있다. 딱총나무의 고갱이에는 같은 모양의 세포들이 유별나게 규칙적으로 쌓여 있다. 이 세포들은 대부분이 14면체이고 나머지는 12, 13, 15, 16면체들인데, 면의 평균 개수는 13.96임이 알려져 있다. 이와 관련돼 19세기 물
리학자 켈빈 경은 3차원 공간의 최적 분할 문제의 해결방안을 다음과 같이 제시했다.

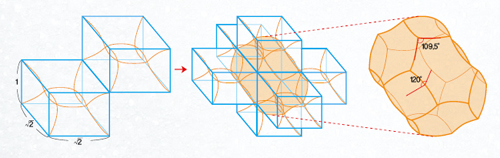
직육면체(밑면은 변의 길이가 2인 정사각형, 높이는 1)의 모서리 형태로 만든 철망을 비눗물에 담갔다 꺼내면 비누거품 막이 생긴다. 이런 직육면체 벽돌을 상하 좌우 앞뒤 각각의 방향으로 하나씩 건너뛴 채 배열해 거품 막을 연결하면 3차원 공간을 같은 모양으로 분할한 거품들이 생긴다. 이 공간분할은 면이 휘어진 벽돌이 반복적으로 쌓인 것이다. 이 벽돌의 표면은 14면체인데, 120°와 109.5°의 구조를 가지므로 벽돌 하나만 놓고 볼 때 넓이가 최소다. 그러나 전체적으로도 최소 넓이인지는 아직 증명되지 않았다.

4 차 원 거 품 에 서 가 능 한 각 도

마지막으로 우리가 살고 있는 3차원 공간보다 차원이 높은 고차원 공간에 대해 생각해 보자. 4차원의 비누거품에는 어떠한 각도가 있는지 알아보기 위해 우선 저차원에서 120°와 109.5°가 어떻게 생겼는지 검토할 필요가 있다. 120°는 2차원 평면의 정삼각형에서 생겼고 109.5°는 3차원 공간의 정사면체에서 생겼다. 그렇다면 4차원 공간에서의 비누거품 각도는 정오입방체에서 찾을 수 있을 것이다.







정오입방체의 중심에서 각 꼭짓점에 이르는 다섯 개의 선분들이 이루는 각도는 얼마일까. 2차원 정삼각형의 120°는 코사인 값이 -1/2인 각도이고 3차원 정사면체의 109.5°는
코사인 값이 -1/3인 각도다. 그러므로 4차원 정오입방체에서 나타나는 각도는 코사인 값이 -1/4이어야 할것이다(이것을 보이는 것은 재미있는 문제이니 한번 생각해 보고 오른쪽 설명(Tip)을 보시오). 이 각도는 바로 104.5°다.

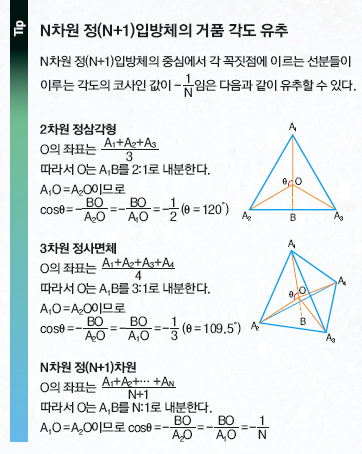
이것을 일반화하면 N차원 공간의 비누거품에서 나타나는 각도는 정(N+1)입방체의 중심에서 생기는 각도이므로 코사인 값이 -1/N이어야 할 것임을 쉽게 유추할 수 있다. 그런데 뜻밖에도 1991년에 4차원 비누거품에서 이와는 다른 새로운 각도가 발견됐다. 평면의 정사각형과 3차원 공간의 정육면체에 대응되는 도형으로 4차원 공간에는 정팔입방체가 있다. 정사각형의 중심에서 네 꼭짓점을 잇는 선분들이 이루는 각도는 90°이고, 정육면체의 중심에서 8개의 꼭짓점을 잇는 선분들이 이루는 각도는 70.5°다. 이들의 반각, 즉 45°와 35.25°의 탄젠트 값은 각각 1/1,1/√2이다.

이 방법을 확장하면 정팔입방체의 중심에서 16개의 꼭짓점을 잇는 선분들이 이루는 각도의 반각은 탄젠트 값이 1/√3임을 어렵지 않게 보일 수있다. 그러므로 이 선분들이 이루는 각도는 다름 아닌 60°다. 2차원 정사각형의 90°, 3차원 정육면체의 70.5°는 비누거품의 각도가 될 수 없으나, 60°는 4차원 비누거품의 각도가 된다는 사실이 18년 전에 발견된 것이다. 아울러 4차원 이상의 N차원 공간에서 정2N입방체에 대응되는 각도도 비누거품에 나타난다는 사실이 증명됐는데, 이 각도의 반각은 탄젠트 값이 1/√N-1이다. 고차원 비누거품에는 이 두 가지 각도 외에 여러 각도가 있을 것이나 아직은 발견되지 않았다.

우리 인생이 한낱 물거품처럼 끝날지는 몰라도, 거품이 오묘한 진리를 담고 있듯이 우리 삶도 신비로운 의미를 품고 있을 것이다










동영상 보기










▼관련기사를 계속 보시려면?

식품 속 거품의 핵심은 계면활성제
딱총나무 세포에서 배우는 거품의 수학
고체 거품 삶의 질 높인다