d라이브러리

‘점’에 속았다고요? 더 놀라운 게 있어요. 선 몇 개로도 놀라운 착시를 만들어 낼 수 있거든요. 과연 어떤 건지, 그 비밀을 지금부터 알려드릴게요.

평행선의 마법사 르네 마그리트

19세기~20세기 벨기에의 화가인 르네 마그리트는 ‘초현실주의’ 화가로 유명해요. 초현실주의란 현실을 초월한 꿈의 세계를 표현하는 예술을 말해요. 마그리트는 우리 눈이 실제 세상과 그림 속 세상을 구분하지 못하도록 착시를 일으키는 작품을 여럿 그렸어요. 이때 ‘평행선’을 이용했지요.

위쪽 그림 속 방 안의 창문이 활짝 열려있어요. 창문 바깥으론 아름다운 들판이 펼쳐져 있는 듯해요. 아니, 잠깐! 눈을 비비고 다시 보니 창가에 이젤이 세워져 있어요. 그림 그릴 때 쓰는 도구인데. 그러고 보니 이젤 위엔 캔버스가 놓여있어요. 그렇다면 우리가 보고 있는 저 풍경은 과연 캔버스 위에 그려진 그림일까요? 아니면 창문 밖 실제 풍경일까요?

우리 눈이 캔버스 속 그림과 창문 밖 풍경을 구분할 수 없는 이유는 바로 평행선 때문이에요. 직사각형 캔버스의 윗변과 아랫변을 이루는 두 개의 평행선은 바깥 풍경 속 평행선과 쭉 이어져 있어요.

오른쪽 그림을 보세요. 원뿔 모양의 건물 지붕 바로 옆에 그와 똑같이 생긴 원뿔이 하나 더 있는 것 같아요. 하지만 자세히 보면 그건 사실 멀리 이어진 큰길이에요. 길을 이루는 두 개의 선이 끝에서 만나, 마치 꼭짓점이 하나 있는 원뿔로 보여요.

고대 그리스의 수학자 유클리드는 평행선을 ‘아무리 길게 늘여도 절대 만날 수 없는 직선’이라고 정의^★했어요. 그런데 원근법을 이용한 그림에서는 두 개의 평행한 직선이 소실점이라는 한 점에서 만나지요. 마그리트는 이렇게 평행선이 미술 속에서는 만날 수 있음을 표현한 거예요. 이 작품 역시 창문 안쪽의 캔버스와 창문 밖 바깥 풍경을 구분할 수 없지요.

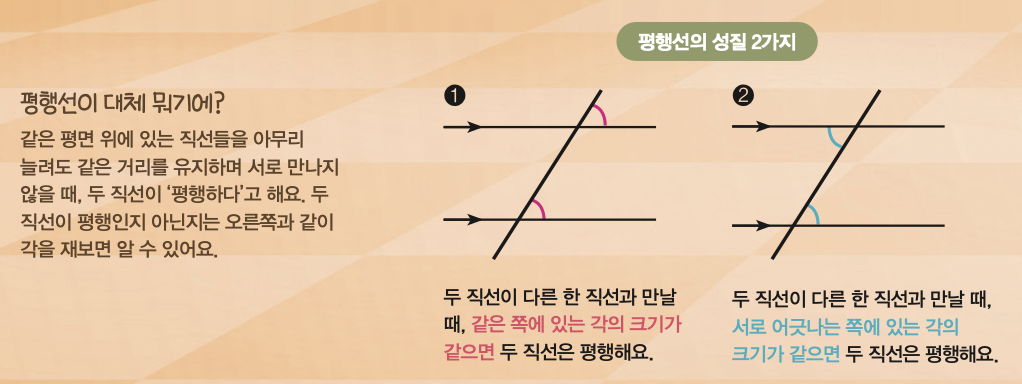
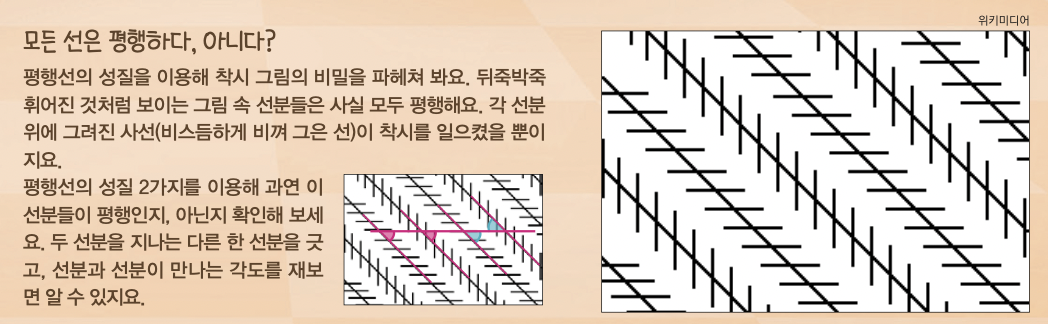
용어 설명

정의^★ 어떤 말이나 사물의 뜻을 뚜렷하게 정하는 거예요.