d라이브러리

0.99999…로 소수점 아래 수가 무한히 이어지면 1이 될까요? 아니면 1보다는 작고 0.99999…보다는 큰 수가 따로 있을까요? 이 질문의 답을 찾기 위해 등비수열과 그 합에 대해서 이야기해볼게요. 

이와 같이 수열의 항이 1/10배씩 줄어들면, 초항이 0.9고 등비가 1/10인 등비수열이 돼요. 0.99999…는 이 등비수열의 합과 같지요. 일반적으로 초항이 a이고 등비가 r이면, n번째 항은 ar^{n - 1}이에요. 이제 등비수열의 합 공식을 유도해볼게요.

여기서 r의 절대값이 1보다 작으면 n이 무한대로 갈 때 rⁿ은 0으로 수렴합니다. 그러면 등비수열의 합은 a/(1-r)이 됩니다. 

처음 봤던 등비수열의 초항은 0.9이고 등비는 1/10이었어요. 이 경우 등비의 절댓값이 1보다 작기 때문에 a/(1-r)에 대입해보면, 아래와 같아요.

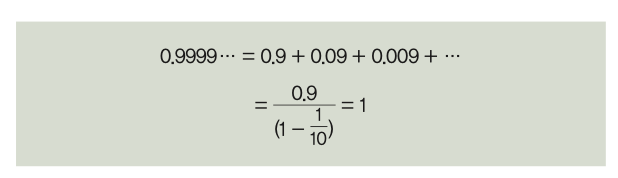
이 등비수열의 합 0.9999…는 1에 수렴해요. 그런데 여기서 수렴한다(converge)는 말의 의미를 조금 더 자세히 알아볼게요. 수렴이란 차이가 한없이 작아져서 특정 값에 한없이 가까워진다는 말이에요. 특정 수열 a_n의 수렴하는 값이 a라는 것을 조금 더 수학적으로 정의해보면 다음과 같아요. 

수학에서 정의를 명확히 하는 까닭은 무엇일까요? 2화에서 언급했지만, 개념을 명확하게 정의해야 그에 관한 수학 명제를 만들 수 있기 때문이에요. 명제가 정확한 표현을 담고 있어야 엄밀하게 증명할 수 있지요. 수렴도 마찬가지입니다.

사실 수학뿐만이 아니에요. 축구에서 골인의 정의를 수학적으로 생각해 볼게요. ‘아주 얇은 종이가 존재해서 그 종이를 좌우 골대 안에 있는 끝 선(end line)에 수직으로 세워서 공이 그 종이를 넘어가면 골인’이라고 할 수 있어요. 실제 축구 경기에선 종이 대신 레이저를 사용해 공이 레이저 빛을 기준으로 어디에 놓였는지를 보고 골인 여부를 판단해요. VAR이라고 부르는 영상을 이용하는 심판 시스템이 나오기 훨씬 이전부터 이 기술을 사용했습니다.

다시 수학의 수렴 이야기로 돌아올게요. 수렴의 영역에서는 그동안 우리가 유한한 대상에 사용했던 수학 공식을 바로 적용할 수 없어요. 공식에 항상 적용이  안 된다는 것은 아니고, 적용할 수 있는지, 없는지를 알아보고 써야 한다는 거예요. 즉 적용할 수 있는 상황에 관한 별도의 증명이 필요하지요. 수학자는 이 모든 것들을 세밀하게 증명해요. 

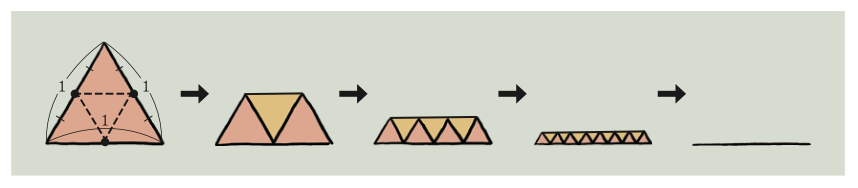
만화에 나오는 삼각형을 계속 접을 때도 접는 횟수가 무한하다면 삼각형의 좌우 윗변은 밑변으로 수렴하지만, 좌우 윗변의 길이의 합은 밑변의 길이로 수렴하지 않아요. 수렴의 영역에서는 이런 이상한 일도 생긴 답니다.

말만 들어도 복잡하지요? 그래도 그런 복잡함이 수학을 더 재미있게 하고 수학자가 진실을 추구하는 기쁨을 더 크게 누리게 한답니다. 그런데 저는 수학이 우리가 사는 세상만큼 복잡하지는 않다고 여겨요. 수학에는 거짓이 자리 잡을 만한 공간이 없으니까요.