d라이브러리

경로 찾기 문제라…. 이건 좀 복잡해 보이는군. 이쪽, 저쪽 경우의 수가 상당히 많은 걸? 후훗. 하지만 나는 이보다 더 어려운 문제도 푼 적이 있지. 어디 한번 시작해 볼까?

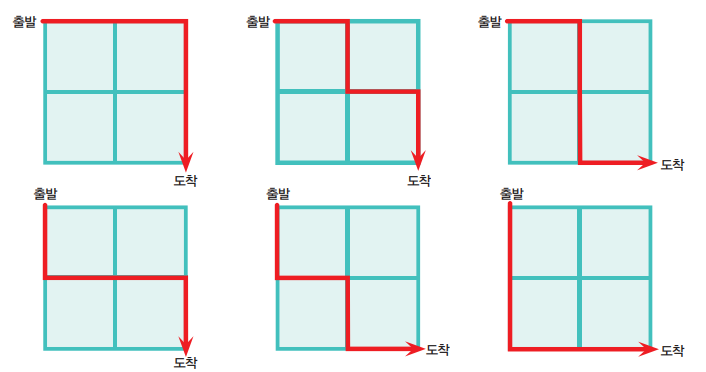
오일러 프로젝트 15번 문제는 격자 위에서 경로를 찾는 것이다. 아래 그림처럼 정사각형이 가로, 세로 2개씩 있는 2×2 격자의 출발점에서 도착점까지 이동하는 방법은 몇 개일까? 이동은 오른쪽과 아래 방향으로만 할 수 있다. 하나씩 따져보면 이동 방법은 아래 그림처럼 총 6가지라는 것을 알 수 있다.

그렇다면 격자의 수를 늘려서 가로, 세로 20개씩 있는 20×20 격자의 왼쪽 위에서 오른쪽 아래 끝부분으로 가는 경로는 총 몇 가지나 될까? 오일러 프로젝트 15번 문제는 바로 이 경우의 수를 계산하는 문제다.

경로 찾기 문제에서 시작된 그래프 이론

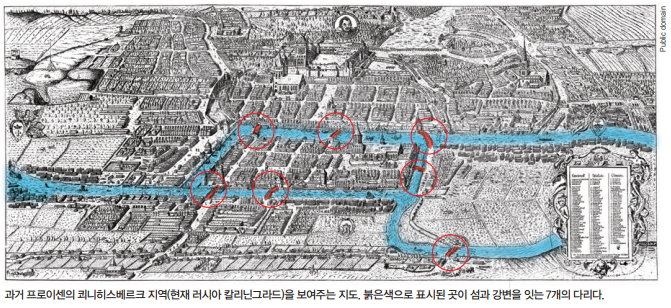
경로 찾기 문제는 레온하르트 오일러가 큰 관심을 가졌던 문제 가운데 하나다. 오일러는 스위스에서 태어났지만 러시아에 살면서 대부분의 연구를 했다. 그가 머물던 쾨니히스베르크 지역에는 도시를 지나는 강에 작은 섬 2개와 섬과 강변을 잇는 다리 7개가 놓여 있었는데, 사람들 사이에서 이 다리를 한 번씩만 건너면서 모든 다리를 건너 제자리로 돌아오는 방법이 있는지를 찾는 문제가 유행했다.

사람들이 답을 찾지 못하자 오일러가 나섰다. 오일러는 섬과 강변을 점으로, 다리를 선으로 나타내 문제를 그래프 형태로 바꿔 단순하게 만들었다. 그래프의 선을 한 번씩만 지나면서 원래의 출발점으로 돌아오는 방법을 찾는 것이다. 오일러는 그 방법이 없음을 증명했다. 오늘날에는 이런 문제를 ‘한붓그리기 문제’라고 부른다.

오일러의 이 연구는 수학에서 ‘그래프 이론’이라는 새로운 분야를 개척했다. 오일러가 의도한 것은 아니었지만 많은 수학자가 오일러의 연구에 관심을 가지면서 새로운 후속 연구가 줄줄이 이어져 수학의 중요한 연구 분야로 자리 잡게 된 것이다.

수학과 공학, 다방면에서 활약하는 그래프 이론

경로 찾기 문제에서 출발한 그래프 이론은 현재 수학뿐 아니라 다양한 과학과 공학 분야에서 활발하게 응용되고 있다. 대표적인 분야가 통신 네트워크와 반도체 회로 설계다. 스마트폰 같은 무선 이동통신을 이용하려면 무선 신호를 전송하는 장치를 전국 곳곳에 설치해야 하는데, 통신사 입장에서는 장치를 효율적으로 설치해서 통신 품질을 가장 좋게 만드는 것이 중요하다. 이처럼 통신 장치를 효율적으로 설치하는 데 그래프 이론을 활용한다.

반도체로 만든 집적회로(위 사진)의 경우 작은 면적에 회로의 폭이 나노미터(nm·10억 분의 1m) 단위로 좁게 복잡한 모양의 회로를 그려 넣어야 한다. 이때 원하는 요소를 포함한 회로를 효율적으로 설계하기 위해 그래프 이론을 쓴다. 

이처럼 경로 찾기 문제는 단순히 점과 선 위에서 길을 찾는 문제에 불과하지만 활용도가 무궁무진하게 넓은 분야라는 걸 생각하며 20×20 격자의 경로 찾기를 풀어 보자.

오일러 프로젝트 15번 문제를 해결하려면?

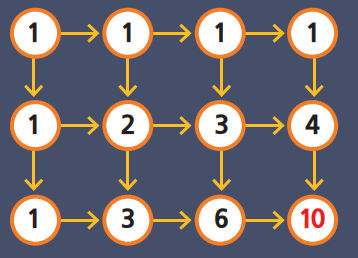
경로 찾기 문제는 어떤 관점으로 보는지에 따라서 여러 가지 해법이 있을 수 있답니다. 가장 많이 쓰는 해법은 각 교차점으로 가는 방법을 차례로 더하는 거예요. 오른쪽 그림을 보면 ‘아하~’ 하면서 무릎을 치는 친구들도 있을 것 같군요.

하지만 20x20 격자를 이렇게 손으로 계산하려면 꽤 큰 종이와 상당한 인내심이 필요할 거예요. 똑같은 계산을 프로그램으로 짜서 컴퓨터에 맡기면 훨씬 편하고 빠르게 답을 구할 수 있답니다. 이때 주의할 점은, 경로의 수를 계산하다 보면 일반적인 정수 범위(32비트)를 넘는 큰 수가 나오기 때문에 ‘큰 수’에 적합한 *자료형을 써야 한다는 점이에요.

위 그림에 나온 격자를 조금 다른 관점으로 한번 볼까요? 출발점에서 도착점까지 가는 어떤 경로를 택하더라도, 그 경로는 항상 오른쪽(→) 3번, 아래쪽(↓) 2번으로 이뤄져 있어요. 예를 들어 ‘→→→↓↓’라든지, ‘→↓→↓→’ 같은 식이죠. 

오일러 프로젝트 15번 문제는 결국 3개의 →와 2개의 ↓를 나열하는 모든 경우의 수를 찾는 거랍니다. 즉 같은 것이 있는 순열의 수로 풀 수 있어요. 순열이란 서로 다른 물건들 중에서 몇 가지를 뽑아 일렬로 나열하는 것을 말해요.

이런 경우의 수를 계산하다 보면 자연수의 계승(팩토리얼, 기호 ‘!’)을 구해야 해요. 어떤 수보다 작거나 같은 수를 모두 곱하는 거에요. 예를 들어 3!은 3×2×1을 뜻합니다. 이때 효율적으로 계산하려면 ‘같은 계산 다시 하지 않기’를 기억하는 것이 좋아요. 예를 들어 5!을 계산할 때 이전에 계산한 4!의 결과 값을 기억하고 있다가 재활용하는 거지요. 이렇게 하면 실행 시간이 획기적으로 단축되기 때문에, 수많은 계산 알고리듬에서 이 기법을 이용하고 있어요.