d라이브러리

인문학자 고대 그리스에서 무한으로 어떤 탐구를 했는지 짧게 살펴봤는데요. 오늘날 수학자는 무한을 어떻게 정의하나요?

수학자 앞서 무한은 수의 개념이 아니라 영원히 끝이 안 나는 상태에 가깝다고 했는데요. 아무리 큰 자연수가 있어도 그 수에 1을 더하면 새로운 자연수가 나타나잖아요. 그래서 가장 큰 자연수를 구하라는 질문에 대답할 수 없어요.

수학에서 이러한 부분을 엄밀하게 다루는 분야를 ‘집합론’이라고 합니다. 수학에서는 무한을 정의할 때 먼저 원소의 개수가 무한한 집합을 찾고, 그 집합의 크기를 무한이라고 이야기해요. 자연수 집합이 대표적이지요.

인문학자 그러니까 무한을 다루기 위해서 적절한 대상의 집합을 설정하고, 그 집합의 크기를 일종의 무한이라고 생각한 거네요. 그 말씀을 듣고 보니까 끝이 없는 무한을 크기로 표현한다는 게 너무 재미있는 생각 같아요. 그러면 더 큰 무한과 더 작은 무한으로 나눌 수도 있을까요?

수학자 그렇죠. 그 부분이 무한을 이해하는 핵심이에요. 자연수 집합 안에 짝수 집합이 포함돼 있어요. 그러면 자연수 집합과 짝수 집합 중 어느 집합이 클까요?

대다수가 아무 의심 없이 자연수 집합이 더 크다고 생각할 거예요. 그런데 두 집합의 크기는 똑같아요. ‘한 집합이 다른 하나를 포함하고 있다’와 ‘한 집합이 다른 집합보다 크다’는 같은 문장이 아니에요.

그렇다면 무한 집합은 어떻게 크기를 비교할까요? 수학자들은 어떤 집합과 다른 집합이 일대일대응이 된다면 이 두 집합의 크기가 같다는 개념을 내세워요.

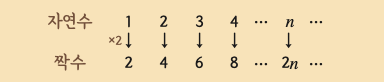
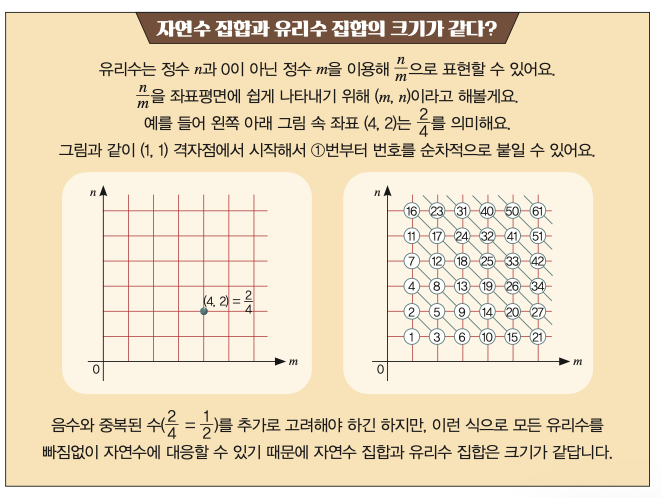
자연수 집합과 짝수 집합을 한번 비교해볼게요. 자연수 집합에서 1, 2, 3, 4에 2를 곱한 짝수를 대응하면 빠지는 숫자가 없이 모두 일대일대응이 돼요. 그렇기 때문에 두 집합의 크기가 같아요.

자연수 집합과 유리수 집합의 크기가 같다는 것도 비슷한 방식으로 보일 수 있어요. 그렇다면 모든 무한 집합은 크기가 모두 같을까요? 놀랍게도 독일 수학자 게오르크 칸토어(1845~1918)가 실수 집합은 자연수 집합보다 크다는 사실을 증명했어요. 더 작은 무한과 더 큰 무한이 존재한다는 거예요. 그리고 이런 무한의 크기조차도 무한하다는 게 현대 수학에서 이해하고 있는 무한입니다.

인문학자  수학자는 복잡한 무한을 어떻게 다루나요?

수학자 예를 들어서 설명해볼게요. A는 자신보다 100m 앞서가는 B보다 2배 빠른 속도로 B를 따라잡으려고 해요. 그런데 A가 100m를 가는 동안 B는 다시 50m를 가고, 이어 A가 50m를 가는 동안 다시 B는 25m를 더 가지요. 이렇게 A가 B를 따라잡으려고 애써도, B 역시 계속 움직이므로 A는 영원히 B를 따라잡을 수 없는 것처럼 보입니다.

이것이 기원전 5세기에 나온 ‘제논의 역설’입니다. 현대 수학을 이용해 이 논리가 틀림을 보일 수 있지만, 19세기 전까지는 이를 깨트릴 방법이 없었습니다.

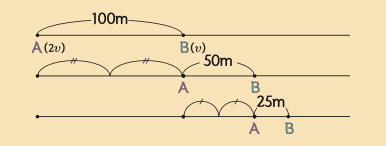
앞서가는 사람이 처음의 절반을 가고 또 절반을 무한히 간다고 생각하면 끝이 없어 보이지만, 수로 나타내면  1/2+1/4 +1/8 +・・・ 이에요. 이를 계산하면 1이라는 아주 간단한 수가 나오기 때문에 언젠가는 A가 B를 따라잡습니다.

이로써 인류는 무한한 덧셈을 걱정할 필요가 없습니다. 무한한 덧셈이라도 유한한 값으로 수렴하면 그 값을 그대로 이해하고 쓸 수 있으니까요. 이렇듯 수학자는 무한급수를 이용해 무한을 다룹니다.

다른 예시를 하나 더 들어볼게요. 수학자가 하는 일 중 하나는 증명이잖아요. ‘1부터 n까지 자연수의 합은 언제나 n(n+1) /2 이다’라는 명제를 증명한다고 생각해보세요. 이 명제가 참이려면 n이 어떤 수이건 모두 참이어야 해요. 이러한 명제를 증명하는 방법 중 하나가 ‘수학적 귀납법’이 이에요. n = 1일 때 성립함을 보이고, n = k일 때 성립한다고 가정한 뒤 n = k + 1이 성립함을 보이면 어떤 무한한 계산이라도 참과 거짓을 증명할 수 있지요.