d라이브러리

‘수학 미술관’ 큐레이터 손인하 기자입니다! 인사할 시간도 없습니다. 여러분은 지금부터 작품 속에 있는 수학을 모두 찾아야 이 미술관에서 탈출할 수 있습니다. 작품은 총 6개! 설명을 잘 읽고 수학 질문의 답을 맞혀보세요.

공원이나 욕실에서 비눗방울 놀이를 할 때 비눗물을 묻힌 막대에 생긴 비누막은 수학적으로 의미가 있어요. 면적이 최소가 되는 ‘극소곡면’이거든요. 라우라 니카 작가는 독일 수학자 하인리히 셰르크가 발견한 극소곡면을 조각품으로 만들었어요.

정답 : 극소곡면

안두리엘 위드마크 작가는 대칭과 패턴에 관심이 많아요. 주로 막대들을 쌓거나 엮어서 작품을 만들지요. 이 작품은 유리 막대 30개로 5개의 사면체를 교차해 만들었어요. 내부가 잘 보이는 것이 특징이에요. 각 꼭짓점을 이으면 한 면이 정오각형인 정십이면체가 나타나요.

정답 : 오각형

양궁의 과녁처럼 보이는 동심원의 각 원 사이에는 수열이 숨어 있어요. 데이비드 라이먼 미국 알비온칼리지 교수는 ‘랭포드 수열’의 수를 각 색에 대응해서 동심원을 26개 만들었어요. 랭포드 수열은 모든 정수 n에 대해 2개의 n 사이에 n개의 수가 있는 수열을 말해요. 예를 들어 (3, 1, 2, 1, 3, 2)는 n이 3인 랭포드 수열로, 3과 3 사이에 3개의 수가 있고, 2와 2사이에는 2개의 수가 있지요. 라이먼 교수는 7가지 색으로 n이 7인 랭포드 수열을 표현했어요. 왼쪽 가장 위에 있는 원을 예로 들어보면 주황색이 2에 해당해요. 두 주황색 원 사이에 노란색 원과 초록색 원이 하나씩 있으니까요.

정답 : 5

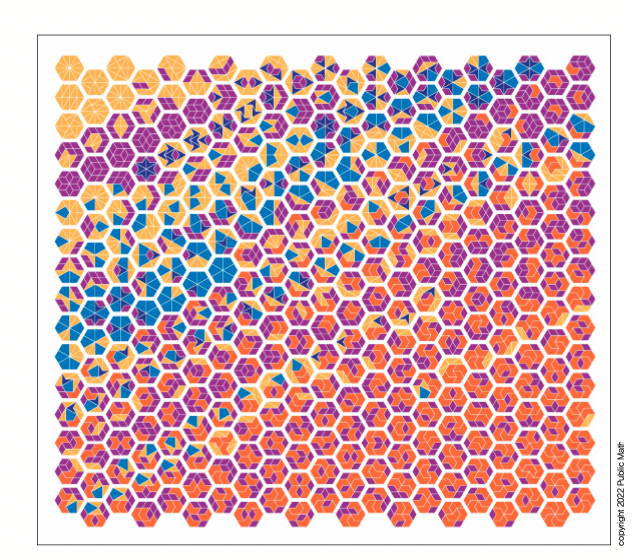
미국의 ‘공동 수학(Public Math) 연구소’는 SNS를 통해 육각형 만들기 챌린지를 진행했어요. 어린이들이 노란색, 주황색, 자주색, 파란색, 남색의 서로 다른 모양의 도형을 직접 조합해 하나의 육각형을 만들어 인증하는 챌린지이지요.

2019년 미네소타주립박람회에서 처음 시작된 이 챌린지에서는 2년 동안 336개의 육각형을 만들었어요. 육각형들을 모두 모아서 이 작품을 만들었지요.

정답 : 사각형

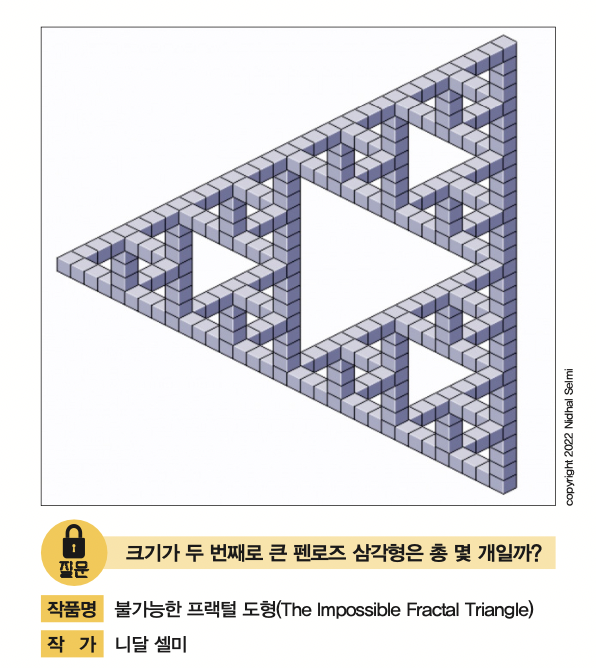
이 작품은 어느 한 지점에서 시작해도 모서리를 따라 쭉 가다 보면 어느새 원래 자리로 돌아옵니다. 이런 구조를 ‘펜로즈 삼각형’이라고 하는데요. 2차원 평면에선 가능해 보이지만, 3차원에서는 절대 만들 수 없는 모양이에요. 니달 셀미 미국 애리조나주립대학교 연구원은 닮은 도형이 반복되는 프랙털과 펜로즈 삼각형에 영감을 받아 펜로즈의 삼각형을 여러 개 이어 붙여서 이 작품을 만들었어요.

정답 : 4

격자무늬 식탁보가 떠오르는 이 작품은 미국 켄터키대학교 수학연구소에서 문자 4개로 이뤄진 집합의 대칭을 표현한 퀼트 작품이에요. 예를 들어 1, 2, 3, 4 이렇게 4개의 숫자가 있을 때 이 숫자를 나열하는 방법의 수는 4 ｘ 3 ｘ 2 ｘ 1 = 24예요. 그 경우의 수를 가로, 세로 각 줄에 서로 다르게 나타내면 24 ｘ 24 크기의 표가 만들어져요. 이 작품은 총 24가지의 색의 천을 바느질해 만들었어요.

정답 : 576개

와, 정말 대단해요. 작품에 숨은 수학을 모두 찾았군요. 작품 속 수학을 속속들이 찾은 여러분에게 2022 수학예술전 미션 완료 티켓을 드릴게요. 내년 전시회에 참여할 수 있는 입장권이랍니다. 다음에 또 만나요!