d라이브러리

11 하면 어떤 생각이 떠오르니? 11처럼 쭉 뻗은 쌍둥이 빌딩, 2011년 11월 11일의 빼빼로와 가래떡, 첫 번째 쌍둥이 수…. 저마다 다른 무언가를 떠올릴 텐데, 특별히 떠오르는 게 없는 친구도 있을 거야. 걱정하지 마. 11로 떠나는 여행이 있으니까. 숫자 11을 향해 출발~!

제1코스 시침과 분침의 움직임을 주목하라
빈칸을 포함한 다음 11개의 시간들은 어떤 규칙으로 이뤄졌을까? 그리고 빈칸에 들어갈 알맞은 시간은 무엇일까?

1:38 2:44 3:49 4:55 (__:__) 7:05 8:11 9:16 10:22 11:27 12:33

아마도 눈썰미가 있는 독자라면 빈칸에 들어갈 시간을 ‘6:00’라고 생각했을 것이다. 이는 1:38과 2:44의 차이가 1:06, 2:44와 3:49의 차이가 1:05, 3:49와 4:55의 차이가 1:06이므로, 두 시간의 차이가 1:06, 1:05가 반복된다고 추측한 게 아닐까. 그런데 빈칸에 6:00을 넣으면 그 다음 시간인 7:05와의 차이가 1:06이 아닌 1:05가 돼 버려서 예상했던 규칙에서 벗어나게 된다.

이는 더 그럴듯한 이유, 즉 다른 규칙이 있다는 얘기다. 무엇일까? 힌트는 아날로그 시계다. 숫자로 표시되는 디지털 시계와 달리 아날로그 시계는 시침과 분침, 초침으로 시간을 연속해 보여준다. 그리고 이 아날로그 시계의 시침과 분침이 이루는 각도가 180°일 때 시간을 반올림해 분 단위까지 나타내면 앞에서와 같은 11개의 시간이 나온다.

이렇게 반올림한 숫자들은 간격이 약간 차이를 보이지만 실제로 분침과 시침이 180°를 이루는 시간 사이의 간격은 항상 일정하다. 반올림하지 않으면 같다는 얘기다. 그 이유는 시침과 분침이 일정한 속도로 움직이기 때문이다.

시계의 움직임을 자세히 살펴보면 정확한 시간 차이를 구할 수 있다. 1시간, 즉 60분마다 시침은 30°씩 움직이고, 분침은 360°씩 움직인다. 이를 식으로 표현하면 x분 뒤에 시침이 움직인 각도는 30/60x=1/2x, 분침이 움직인 각도는 360/60x=6x, 따라서 시침과 분침사이의 각도의 변화량은 6x-1/2x이다.

처음 시침과 분침이 180°를 이룬 뒤 다시 180°를 이루려면 이 변화량이 한 바퀴, 즉 360°가 돼야 한다. 실제로 분침이 시침보다 빨리 움직이기 때문에 시침과 분침이 처음으로 180°를 이룬 뒤에는 움직임이 더 빠른 분침이 시침을 따라잡는다. 그리고 분침과 시침이 만난 뒤에는 다시 분침이 시침을앞서 나간다.

따라서 다시 180°가 되는 시각은 방정식 6x-1/2x=360을 만족시키는 x의 값에서 찾을 수 있다. 이 방정식의 해를 구하면 x=720/11분이다. 즉 시침과 분침이 처음 180°를 이룬 뒤 다시 180°를 이루는 데는 항상 1시간 60/11분이 걸리는 것을 알 수 있다.
 

tip
11번째 시간

‘11번째 시간(The 11th Hour)’은 영화배우로 유명한 레오나르도 디카프리오가 제작하고 조연으로 참여한 환경 다큐멘터리 영화다. 칸 국제영화제 2007년 특별상영작인 이 영화의 제목은 지구에 남겨진 시간을 12시간으로 봤을 때, 현재는 마지막 기회에 해당하는 11번째 시간이라는 의미를 가지고 있다. 지구온난화의 심각성을 알리고, 이를 극복하기 위해 우리의 결단을 촉구하는 메시지를 담고 있다.

제2코스 숫자의 데칼코마니, 회문수
 

회문수는 대칭수라고도 하며, 123321처럼 순서대로 읽었을 때와 거꾸로 읽었을 때 똑같은 수를 말한다. 11은 회문수이면서 동시에 소수이기 때문에 회문 소수라고 불린다. 소수는 1과 자기 자신으로만 나눠떨어지는 수를 말한다.

회문 소수에는 다음과 같은 수들이 있는데, 신기하게도 11 외에는 모두 한 자리나 세 자리, 다섯 자리 등 홀수 자리로 이뤄진 것을 확인할 수 있다.

2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919,
929, 10301, 10501, 10601, 11311, …

실제로 짝수 자리를 가지는 회문 소수는 11밖에 없다. 짝수 자리로 이뤄진 회문수는 모두 11의 배수이기 때문이다. 예를 들어 44, 3773, 261162처럼 짝수 자리로 이뤄진 회문수는 모두 11의 배수다. 그런데 이 수들이 11의 배수인 것을 어떻게 알까? 직접 나눠보지 않고도 쉽게 알아내는 방법이 있을까?바로 홀수 자리 수의 합과 짝수 자리 수의 합의 차를 확인하는 방법이 있다. 그 둘의 차가 0 또는 11의 배수면 그 수는 11의 배수고, 그렇지 않으면 11의 배수가 아니다. 이런 방법을 11의 배수 판정법이라고 한다.
예를 들어 주어진 수가 의 네 자리 수인 경우, 다음과 같이 나타낼 수 있다.

ABCD=A×10³+B×10²+C×10+D=A×(10³+1-1)+B×(10²-1+1)+C×(10+1-1)+D
= A×(10³+1)+B(10²-1)+C(10+1)-(A-B+C-D)
 

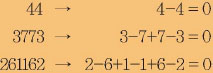
이때 10³+1이나 10¹+1과 같이 10의 홀수제곱에 1을 더한 값은 항상 11의 배수다. 또 10²-1과 같이10의 짝수제곱에서 1을 뺀 값도 항상 11의 배수다. 이 때문에 밑줄 친 부분은 모두 11의 배수다. 따라서 ABCD가 11의 배수가 되려면 A-B+C-D, 즉 홀수 자리 수인 A와 C의 합과 짝수 자리 수인 B와 D의 합의 차가 0또는 11의 배수가 돼야 한다. 이 방법으로 44, 3773, 261162의 홀수 자리 수의 합과 짝수자리 수의 합의 차를 구하면 모두 0이 된다. 따라서 모두 11의 배수가 된다는 것을 알 수 있다. 혹시라도 의심이 된다면 11로 나눠보면 된다. 이처럼 짝수 자리로 이뤄진 회문수 중에서 11이 아닌 수는 모두 11을 약수로 가지는 합성수다. 따라서 짝수 자리로 이뤄진 회문수 중에서 11을 제외하면 회문 소수는 존재하지 않는다.
 

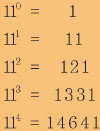
11을 곱해서 회문수를 새로 만들 수도 있는데, 11을 제곱하면 121, 11을 3제곱하면 1331, 11을 4제곱하면 14641로 연달아 회문수가 만들어진다. 11은 0제곱부터 4제곱까지가 회문수다.
 

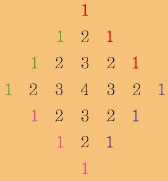
여기서 잠깐 회문수와 관련된 퀴즈를 풀어보자. 다음 그림에서 1234321의 순서대로 지날 수 있는 경로의 수는 모두 몇 가지일까? 단, 한 숫자에서 다음 숫자로 이동할 때는 상, 하, 좌, 우, 대각선 방향으로 1칸씩만 움직일 수 있다.

다음과 같이 자유자재로 이동할 수도 있고, 이미 지나간 숫자를 다시 지나가도 된다.
 

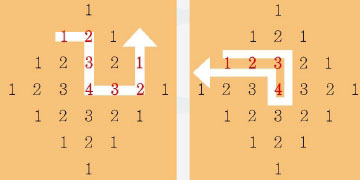
정답은 784가지다. 어떻게 알 수 있을까? 위 그림에서 4라는 숫자는 1개밖에 없으므로 1234321의 순서대로 통과하려면 12개의 1에서 1을 1개 선택해 1, 2, 3, 4의 순서대로 한가운데의 4까지 간 뒤 다시 4에서 4, 3, 2, 1의 순서대로 이동하면 된다. 따라서 1에서 4까지 가는 방법의 수를 제곱하면 된다.

이때 아래 그림처럼 4등분해 생각하면 1에서 4까지 가는 방법의 수를 더 간단하게 구할 수 있다.먼저 붉은색으로 된 1에서 4까지 가는 방법의 총 경우의 수를 직접 경로를 그려서 구하면 7(=1+3+3)가지다. 따라서 1에서 4까지 가는 총 방법의 수는 28(=7×4)가지가 된다. 그러므로 정답은 ${28}^{2}$, 즉 784가지다.
 

X note
1에서 9까지의 배수판정법

2의 배수 : 일의 자리 수가 0이거나 2의 배수이면 그 수는 2의 배수다.
3의 배수 : 각 자리 수의 합이 3의 배수이면 그 수는 3의 배수다. 예를 들어 702는 7+0+2=9가 3의 배수이므로 이 수는 3의 배수다. 반면 326은 3+2+6=11이 3의 배수가 아니므로 이 수 또한 3의 배수가 아니다.
4의 배수 : 십의 자리 이하의 수가 4의 배수이면 그 수는 4의 배수다. 예로 724에서 24는 4의 배수이므로 이 수는 4의 배수다. 반면 8150에서 50은 4의 배수가 아니므로 이 수는 4의 배수가 아니다.
5의 배수 : 일의 자리 수가 0 또는 5이면 그 수는 5의 배수다.
6의 배수 : 6은 2×3과 같으므로 2의 배수이면서 동시에 3의 배수인 수는 6의 배수다.
8의 배수 : 백의 자리 이하의 수가 8의 배수이면 그 수는 8의 배수다. 예로 7816에서 816이 8의 배수이므로 이 수는 8의 배수다. 반면 1436에서 436이 8의 배수가 아니므로 이 수는 8의 배수가 아니다.
9의 배수 : 각 자리 수의 합이 9의 배수이면 그 수는 9의 배수다. 예로 1881은 1+8+8+1=18이 9의 배수이므로 이 수는 9의 배수다. 반면 271은 2+7+1=10이 9의 배수가 아니므로 이 수는 9의 배수가 아니다.

제3코스 주민등록번호에 숨은 체크숫자의 비밀
 

주민등록번호는 13자리의 숫자로 이뤄져 있다. 이 중 앞의 6자리의 숫자는 태어난 생년월일을 뜻하고,뒤의 7자리는 성별과 태어난 지역 등을 숫자로 표현하고 있다.

뒤의 7자리 숫자를 자세히 살펴보자. 우선 첫 자리 숫자는 성별을 나타낸다. 1과 3은 남자, 2와 4는 여자를 의미하는데, 2000년 이후에 태어난 남자와 여자가 각각 3과 4의 숫자를 사용한다. 그 다음 4자리는 태어난 시·도·구·군을 가리키는 지역번호다. 6번째 숫자는 해당 지역에서 주민등록번호 발행 순서를 나타내며, 마지막 숫자는 체크숫자다. 인터넷에서 어떤 사이트에 가입하거나 정보를 입력할 때 실명확인을 할 경우 주민등록번호를 입력하게 되는데, 이때 주민등록번호에 오류가 있는지 확인하는 방법도 이 체크숫자가 만들어진 원리를 이용한다.

마지막 체크숫자를 정하는 원리는 다소 복잡한 편인데, 다음과 같은 여러 단계를 거친다. 13자리 주민등록번호 중 앞의 12자리는 태어난 때와 성별, 장소에 따라 이미 정해진 상태다. 앞의 12자리의 각수에 차례로 2, 3, 4, 5, 6, 7, 8, 9, 2, 3, 4, 5를 곱해 합을 계산한다. 이렇게 계산한 합을 11로 나눠 나머지를 구한다. 그런 다음 11에서 이 나머지를 빼면 그 수가 바로 마지막 13번째 체크숫자가 된다. 이 값이 10일 때는 0, 11일 때는 1이 체크숫자다.

예를 들어 123456-789012□라는 주민등록번호가 있다고 생각해보자(실제 이런 주민등록번호는 없다). 먼저 각 자리마다 순서대로 가중치 2, 3, 4, 5, 6, 7, 8, 9, 2, 3, 4, 5를 곱해 합을 구하면 272가된다.

(1×2) + (2×3) + (3×4) + (4×5) + (5×6) + (6×7) + (7×8) + (8×9) + (9×2)
+ (0×3) + (1×4) + (2×5) = 272

이렇게 구한 272를 11로 나누면 나머지는 8이 된다. 따라서 마지막 체크숫자는 3(=11-8)이다. 그런데왜 하필이면 이 과정에서 11을 사용하는 것일까?

그 이유는 11이 10보다 큰 소수 11, 13, 17, … 중 가장 작은 수라는 사실에서 찾을 수 있다. 체크숫자의 목적은 주민등록번호에 오류가 발생했을 때, 이것을 최대한 정확하고 효과적으로 찾는 것이다. 따라서 잘못된 주민등록번호가 발생했을 때, 이것을 알아차리지 못하는 확률이 낮을수록 유리하다.

예를 들어 주민등록번호 13자리 중 1자리를 a에서 b로 잘못 입력했을 때, 체크숫자로 이 사실을 못 알아차리는 경우를 생각해보자. a가 차지하는 자리에 곱하는 가중치를 k라고 하면, 나머지 숫자는 모두 같으므로, 원래 주민등록번호와 잘못된 주민등록번호에 각각 가중치를 곱해서 얻은 합의 차는k(a-b)가 된다.

이때 체크숫자로 이 사실을 알아차리지 못하는 경우 중 한 가지는 그 차인 k(a-b)가 11의 배수가 될 때이다. 하지만 주민등록번호와 체크 숫자의 기본 원리에 의해 k는 2 이상 9 이하의 자연수이고, a-b는 0을 제외한 -9 이상 9 이하의 정수이다. 따라서 둘을 곱해도 11의 배수가 되는 경우는 발생하지 않는다.

여기서 왜 11이라는 소수가 유용한지 알 수 있다. 만약 그 수가 소수가 아닌 합성수였다면 k와 a-b의곱으로 표현될 확률이 높아진다. 그만큼 체크숫자로 쓰기에 좋지 않은 수가 된다. 또 소수라 하더라도 10보다 작으면 k(a-b)의 배수가 될 가능성이 있기 때문에 역시 좋지 않다.

하지만 k(a-b)가 11의 배수가 아니어도 오류를 알아차리지 못하는 경우가 있다. 어떤 경우일까? 11이10보다 크다는 점에서 나오는 문제인데, a일 때 가중치를 곱한 합을 11로 나눈 나머지가 0이고, b일 때 가중치를 곱한 합을 11로 나눈 나머지가 10일 때이다. 이것이 문제가 되는 것은 11-0=11과 11-10=1에서 두 경우 모두 체크숫자가 1이 되기 때문이다. 따라서 이런 상황에서는 체크숫자를 이용해도 주민등록번호의 오류를 발견할 수 없다. 이와 같은 현상은 나머지가 반대로 10과 0이 될 때도 마찬가지이다.

그런데 이런 오류가 발생할 확률은 10보다 큰 소수 중에서 11을 사용할 때, 가장 낮아진다. 실제로 11 대신 다른 소수를 사용하면, 그 소수가 클수록 오류가 발생할 확률도 커진다. 예를 들어 11 대신 소수 13을 사용했을 때 이와 같은 오류가 발생하는 경우를 살펴보자. 결국 위의 가정과 같이 다른 숫자 a, b로부터 같은 체크숫자가 나오는 경우를 구하면 된다. 이런 경우는 원래 주민등록번호와 잘못된 주민등록번호로부터 구한 나머지가 각각 (0, 10), (10, 0), (1, 11), (11, 1), (2, 12), (12, 2)일 때인 6가지인데, 소수 11을 사용한 경우의 수와 비교하면 3배로 더 늘어난다. 결국 소수 11은 주민등록번호의 체크숫자가 오류를 잘 잡아내도록 도와주는 일등공신임에 틀림없다.

숫자 11에 대한 여행을 마친 소감이 어때? 머리에 쥐 나는 줄 알았다고? 숫자가 많이 나와 힘들었다고? 개인마다 느낌이나 경험이 다를 거야. 똑같은 여행이라도 사람마다 생각하는 바가 다르고 보는 게 다르기 때문에 경험도 달라지지. 그래도 숫자 11하면 떠오르는 게 많아졌을 거라고 생각해. 숫자 11이 들려준 이야기를 오래 기억하길 바랄게.