d라이브러리

오늘의 마지막 사연은 '한국의 인디아나 존스'를 꿈꾸는 구독자 안디안 님께서 보내주셨습니다. "우리나라에는 수학 문화재가 많지 않을 뿐더러, 오래된 유물은 쓰임새조차 알기 어려운데요. 유물에 수학적인 내용이 담겨 있는지 어떻게 알 수 있나요? 수학적인 가치를 알아보지 못하면 버려질 수도 있잖아요."

문화재와 수학 이야기에서 수학 문화재를 빼놓을 수 없죠. 질문처럼 우리나라에는 수학 문화재가 많지 않은 편입니다. 예를 들어 중국과 일본에서는 이미 오래 전부터 구구단을 외웠던 기록이 남아 있는데 우리나라에서는 발견된 적이 없었죠. 그래서 과거 중국이나 일본보다 수학이 뒤처졌을 거라고 말하는 사람들도 있었습니다.

하지만 그렇지 않습니다. 한국에서도 7세기 초 백제시대에 이미 구구단을 외우고 활용했던 기록이 발견됐거든요. 구구단이 기록된 목간(나무판)입니다. 일본에서 발견된 구구단 기록보다 훨씬 앞선 기록이어서 변명의 여지없이 구구단이 중국에서 한국을 거쳐 일본으로 전파된 것이 확인된 겁니다.

하지만 이 구구단 목간은 그 수학적인 가치가 밝혀지지 못할 뻔했습니다. 2011년 백제의 도읍지였던 충청남도 부여군에서 발견됐지만, 5년이 지난 2016년에야 구구단이 기록됐다는 것을 알게 됐거든요.

사정은 이렇습니다. 유물을 처음 발견한 건 한국문화재재단의 조사팀이었습니다. 당시 현장에서 나무판 세 개가 나왔는데, 백제시대 목간이라고 추정할 뿐 적힌 내용을 알아보기가 어려웠습니다. 적외선 촬영을 통해 한자가 쓰여 있었다는 것을 어렴풋이 알 수 있었지만 판독할 수 있는 글자가 별로 없었습니다. 그렇게 발견된 목간에 어떤 내용이 담겼는지는 알지 못한 채로 보관됐습니다.

우리나라에서 가장 오래된 구구단 기록 발견!

5년이 흐른 2016년. 당시 국립미륵사지 유물 전시관장이었던 이병호 국립중앙박물관 전시과장은 한 학회에서 2011년 부여에서 발굴된 목간에 대한 발표를 듣던 중 적외선 사진에 유독 눈길이 갔습니다. 제대로 보이는 글자가 거의 없었지만 아랫부분에 있는 글자가 마치    ‘三四十二(3×4=12)’라고 쓰여 있는 것 같았습니다.

 집으로 돌아와 초등학생이었던 아들과 함께 목간 사진을 뚫어져라 쳐다보며 나머지 희미한 글자를 판독해 본 이 전시과장은 목간이 구구단을 써놓은 것이라는 확신이 들었습니다. 三四十二 바로 옆에 ‘四:十六(4×4=16)’이 보였고, 다른 숫자들도 눈에 들어왔기 때문입니다. ‘매의 눈’과 구구단에 대한 기초적인 지식이 한국에서 가장 오래된 구구단 유물을 밝힌 순간이었습니다.

이 전시과장을 비롯한 여러 학자들이 분석한 결과 이 목간에 적힌 103자 중에서 98자를 판독할 수 있었고 구구단을 기록한 것이라는 주장이 분명해졌습니다. 특히 구구단 목간은 굉장히 규칙적으로 기록돼 있었습니다. 역삼각형 모양의 직각 부분에 해당하는 부분부터 시작해 아래 방향으로 9단, 8단, 7단의 순서로 기록됐고, 수평 방향으로 행을 나누는 선을 그어 각 단을 구분했습니다.

또 현재와 다르게 9×9=81, 8×9=72, 7×9=63 같은 순서로 표기했고, 특히 8×9=9×8처럼 위에서 한 번 등장한 계산은 생략하는 효율적인 표기법을 도입했습니다. 그러다 보니 아래 단계로 내려올수록 표기할 숫자가 줄어들어 자연스럽게 역삼각형 모양이 만들어졌습니다. 목간 모양이 우연히 삼각형 모양이 아니라 일부러 삼각형 모양으로 자른 것이라고 추측할 수 있는 대목입니다. 

이 전시과장은 “보통 목간은 사각형인데 이 목간만 삼각형”이라며, “사각형 모양의 나무판을 삼각형 두 개로 잘라서 두 개의 구구단 목간으로 만들어 썼을 수도 있다”고 말했습니다.

바빌로니아인이 삼각비를 알았을까?

수학 유물 중에는 내용이 명확한 것도 있지만 해석의 여지가 많은 것들도 있습니다. 이런 경우에는 학자들의 분석과 상상력이 동원돼 해석이 이뤄집니다. 그러다 보니 해석을 두고 논란이 벌어지기도 하죠.

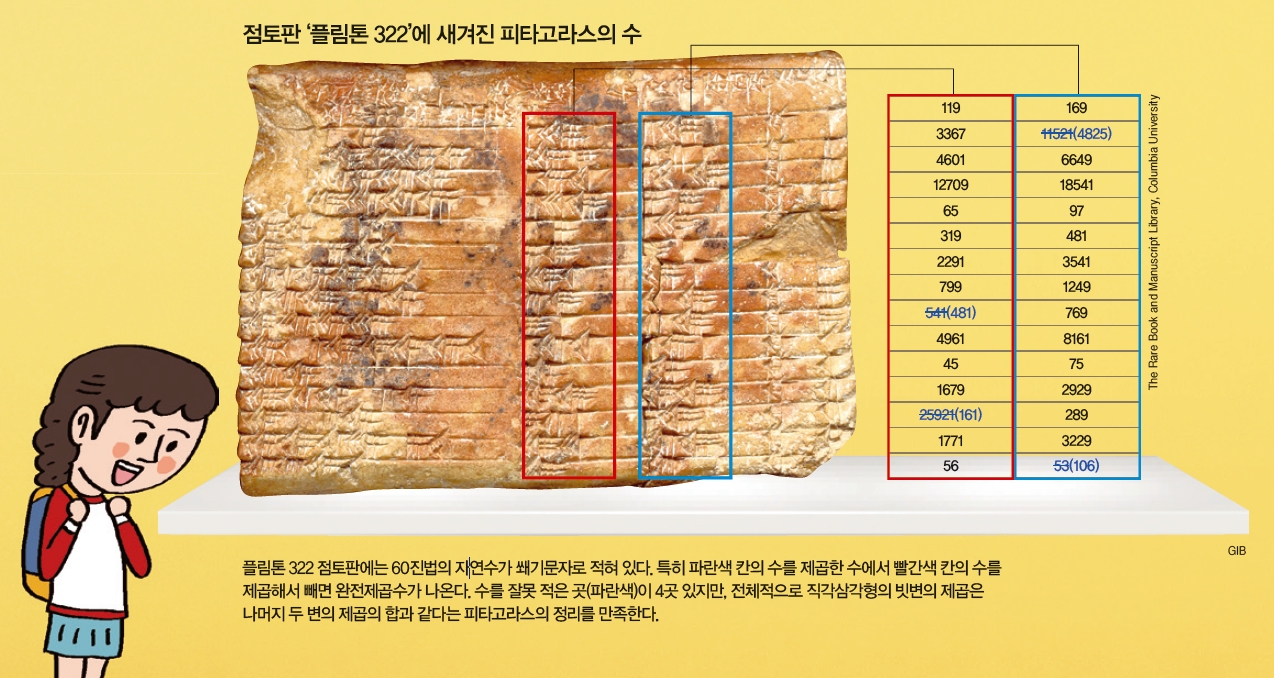
기원전 1800년경 고대 바빌로니아인이 만든 것으로 추정되는 점토판이 대표적인 사례입니다.  ‘플림톤 322’라는 이름이 붙은 점토판에는 각각 15줄씩 4단락으로 나뉘어 쐐기문자가 적혀 있는데 학자들은 이를 60진법의 자연수라고 해석했습니다. 특히 1940년대에는 이 점토판에서 ‘직각삼각형에서 직각을 낀 두 변의 제곱의 합은 빗변의 제곱과 같다’는 ‘피타고라스의 정리’를 만족하는 수들이 확인됐습니다.

2017년에는 호주 뉴사우스웨일즈대학교의 대니얼 맨스필드 교수와 노먼 윌드버거 교수가 플림톤 322에 적힌 수들이 일종의 삼각비 표라는 주장을 제기하는 논문을 수학사 학술지 ‘히스토리아 마테마티카’에 발표하기도 했습니다. 피타고라스의 정리를 만족하는 수들이 적혀 있기 때문에 그 내용을 통해 직각삼각형의 각 변 사이의 길이의 비인 삼각비를 알 수 있다는 겁니다. 맞는 말이지만 점토판 어디에서도 삼각비를 공식으로 표현한 관계식이 있는 것은 아니기 때문에 정말 바빌로니아인들이 삼각비 개념을 알고 점토판을 삼각비 표로 사용했는지에 대해서는 의견이 분분한 상황이죠.

문화재를 주제로 한 ‘문화재 님 안녕하세요?’ 방송은 여기까지입니다. 어떠세요? 평소에 굳이 궁금하지 않았던 것까지 해결할 수 있었던 시간이었죠? 그게 바로 저희 방송의 매력이죠! 전혀 수학과 관련 없어 보이는 고민과 질문도 모두 수학으로 해결해 드릴 수 있으니 언제든 사연을 보내 주세요. 자, 그럼 저는 다음 상담 시간에 다시 여러분을 찾아뵙겠습니다. 감사합니다