d라이브러리

인테리어에서 가장 고민한 부분은 바로 벽지야. 벌써부터 내 방 벽지가 실제 어떤 모습일지 정말 궁금한 거 있지? 수학적으로 고른 무늬거든! 벽지를 수학적으로 골랐다니 무슨 뚱딴지같은 말이냐고?

수학자들은 평면을 채울 수 있는 반복 무늬가 대칭성을 기준으로 17가지로 나뉜다는 것을 알아내고 여기에 ‘벽지군(평면의 대칭군)’이라는 이름을 붙였어요. 즉, 벽지의 무늬를 수학적으로 분류할 수 있다는 거예요.

벽지군은 벽지 무늬가 17가지밖에 안 된다는 뜻은 아니에요. 실제 눈으로 보이는 무늬는 다르더라도 대칭이라는 기준을 놓고 보면 평면을 채우는 모든 종류의 무늬를 평행사변형의 기본 무늬를 변환하는 방식으로 17가지로 분류할 수 있다는 뜻이죠.

벽지군은 평면을 채우는 반복 무늬의 종류를 총 17개의 대칭군으로 분류한 거예요. 대칭군은 특정 변환에 대해 대칭인 무늬들을 모은 집합이라고 할 수 있어요. 예를 들어 평행이동을 하거나 반사 변환을 해서 원래대로 만들 수 있는 무늬들은 모두 같은 대칭군이라고 할 수 있죠.

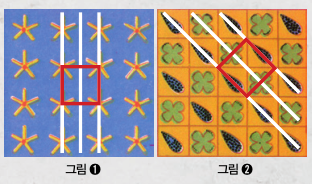
그럼 17가지 벽지군은 어떻게 구분할 수 있을까요? 쉬운 예를 들어 볼게요. 오른쪽 그림 ①, ②는 기본적으로 붉은색 평행사변형(여기서는 정사각형)을 기준으로 평행이동 변환을 해서 평면을 가득 채울 수 있어요. 여기에 흰색 선을 기준으로 반사 변환을 해서 같은 모양으로 평면을 채울 수도 있죠. 따라서 무늬는 다르지만 같은 벽지군입니다. 이런 식으로 다양한 변환에 대해 총 17가지 군으로 벽지 무늬를 분류할 수 있어요.

이 17가지 벽지군을 한 자리에서 모두 감상할 수 있는 건축물이 지구상에 딱 한 곳, 스페인에 있습니다. 바로 그라나다에 있는 알함브라 궁전이에요. 벽지군이 17가지라는 것이 증명된 19세기보다 5세기나 앞선 1300년대에 완성된 건물인데도 곳곳에 새겨진 아름다운 무늬에서 17가지 벽지군을 모두 발견할 수 있다니, 정말 대단하지 않나요?