d라이브러리

빈틈없이 효과적으로 트럭을 채운 짐과 함께 우리 가족은 배를 타고 새로운 집으로 향했어. 집에 도착해 예쁘게 도배가 된 내 방을 보니 빨리 짐을 옮겨 놓고 싶은 거 있지? 그런데 매스 익스프레스 아저씨들은 짐을 옮기기는커녕 복도에서 길이를 재고 계시네. 이번에는 또 무슨 일이지?

이사의 마지막 단계는 트럭에 싣고 온 짐을 빼서 새 집에 배치하는 거예요. 이때 가장 중요한 것은 물건에 흠집이 생기거나 망가지지 않도록 조심해서 나르는 거죠. 그런데 수학자들은 이런 상황을 두고도 수학을 생각해냈답니다.

좁은 복도에서 사다리 옮기기

먼저 쉬운 사다리부터 옮겨 볼게요. 폭이 1m인 좁은 아파트 복도가 ‘ㄱ’자 모양으로 나 있다고 생각해 보세요. 이 통로에서 옮길 수 있는 가장 긴 사다리의 길이는 얼마일까요? 단, 사다리의 두께는 고려하지 않고, 휘지 않은 직선 사다리만 생각할게요. 또 그림처럼 2차원 평면에서 움직이는 사다리만 고려할게요.

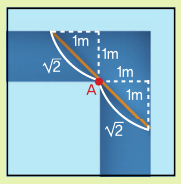
정답이 증명되지 않은 소파 옮기기 문제

자, 그럼 이번에는 좀 더 복잡한 물건을 옮겨 볼까요? 이제 90°로 꺾인 1m 폭의 복도에서 소파를 옮길 거예요. 평면에서 옮길 수 있는 가장 넓은 면적을 가진 소파의 모양은 무엇일까요?

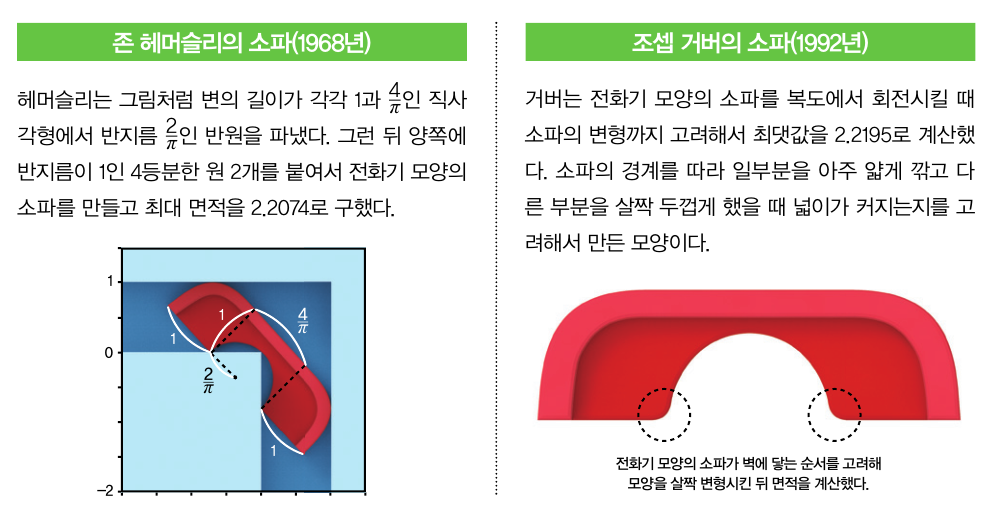
이 문제는 아직까지 정답이 증명되지 않은 ‘소파 옮기기 문제’입니다. 1966년 캐나다의 수학자 레오 모저가 제시한 문제죠. 1968년에 영국 수학자 존 헤머슬리가 자신 있게 2.2074라는 답을 내놨어요. 복도에서 소파를 돌리는 상황을 생각했을 때 전화기 모양의 소파가 최적이라고 생각한 거죠. 하지만 헤머슬리가 계산한 값보다 더 큰 값이 1992년에 나왔어요. 조셉 거버라는 미국 수학자가 가장 큰 값이 2.2195라는 결과를 제시한 거죠. 하지만 아직 이 값이 최댓값인지 아닌지 몰라요. 더 큰 면적을 갖는 소파 모양이 있을 수도 있을까요? 

백진언 국가수리과학연구소 연구원은 현재 거버가 계산한 값이 맞는지를 확인하는 연구를 하고 있어요. 컴퓨터 프로그램을 만들어서 소파가 벽에 어떻게 닿는지를 확인해 모양을 검증해 보는 방식이죠. 백 연구원은 “최적의 모양 자체가 워낙 복잡해서 증명을 하기가 쉽지 않다”고 말했어요.

피아노만 옮기면 이사 끝!

이제 이사의 ‘끝판왕’이라고 할 수 있는 피아노를 옮길 차례입니다. 피아노는 무게도 무겁지만 크고 모양이 복잡한 악기여서 나르기가 쉽지 않아요. 피아노만 전문적으로 운반하는 사람들이 있을 정도죠. 피아노를 옮기는 모습을 보면 한 편의 곡예를 보는 것 같답니다.

그 모습이 인상적이었는지 학자들은 ‘피아노 운반 문제’라는 걸 만들었어요. 제한된 공간에서 특정 지점에 놓인 물체를 원하는 지점까지 이동시킬 수 있는 연속적인 경로가 있는지를 묻는 문제예요.

이 문제는 조건에 따라 공간의 형태가 달라지기 때문에 일반적인 풀이가 있는 것은 아니에요. 특히 경로가 있지 않다는 것을 보이려면 가능한 모든 경로를 확인해야 하는데, 현실적으로 이를 확인하기는 어려워요. 그래서 공학자들은 최적의 답을 찾아 주는 몇 가지 효율적인 알고리듬을 이용해서 풀고 있습니다.

로봇과 게임 개발에 빠질 수 없는 문제

이름만 보면 재미 삼아 만든 문제처럼 느껴질 수 있지만 피아노 운반 문제는 로봇공학과 게임 개발 등 다양한 분야에서 동작을 계획하는 데 아주 중요하게 쓰이고 있어요. 현대 공학에서 피아노 운반 문제는 ‘동작 계획’이라는 문제로 발전해 활용되고 있어요.

동작 계획이란 현재 위치에서 목표 위치까지 움직일 수 있는 최적의 움직임을 계획하는 걸 말해요. 예를 들어 로봇이 무거운 상자를 옮기거나, 게임 속에서 움직이는 캐릭터가 장애물을 피해서 사용자가 원하는 지점으로 이동하게 하려면 피아노 운반 문제를 풀어야 해요. 전재욱 성균관대학교 전자전기공학부 교수는 “피아노 운반 문제는 대표적인 동작 계획 문제”라며, “한정된 자원을 이용해 A 지점에서 B 지점으로 이동하는 방법을 찾는 것”이라고 설명했어요.

그럼 공학자들은 이 문제를 어떻게 풀까요? 실내 자율주행 로봇을 예로 들어 볼게요. 로봇은 우선 공간을 탐험하면서 각종 센서를 이용해서 공간에 대한 지도를 그려요. 그런 뒤 센서를 통해 지도에서 자신의 위치가 어디인지를 파악하고 목적지까지의 최단 경로를 계산해서 움직이죠.

최단 경로를 계산하는 방법은 다양해요. 그 중 잘 알려진 ‘A*’라는 알고리듬을 예로 들면 지도를 좌표 평면의 점과 선으로 이뤄진 격자로 변환해서 최단 경로를 구하는 거예요. 로봇의 동작 알고리듬을 연구하는 김순겸 한국과학기술연구원 선임연구원은 “로봇이 움직일 수 있는 여러 점들에 대해서 출발지로부터 이동한 거리와 목적지까지 가는 거리의 예측값의 합을 비교하면서 최적의 경로를 찾는 방식”이라고 설명했어요.

우와~. 피아노까지 옮기고 나니 이사가 다 끝났어! 이사를 하면서 이렇게 많은 수학 이야기를 알게 될 줄이야. 이사와 관련된 수학 문제가 이렇게 많은 곳에 쓰인다는 것도 정말 놀라워. 이제 보니 아저씨들 옷에 적힌 매스 익스프레스라는 문구의 뜻이 뭔지 알 것 같아. 수학으로 신속, 정확, 완벽하게 이사를 도와준다는 뜻 아닐까!

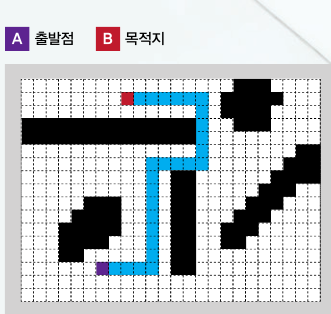
● A* 알고리듬에서 실내 자율주행 로봇이 장애물을 피해 목적지까지 가장 효율적으로 이동하는 경로를 찾는 방법이다. A 지점에 있는 로봇이 B 지점까지 이동하기 위해서는 먼저 지도를 좌표 평면에 나타낸다. 그런 뒤 좌표 평면에서 장애물을 움직일 수 없는 지점으로 설정하고 지나갈 수 있는 곳을 연결한 선을 따라 목적지까지 이동하는 최단 경로를 계산한다.