d라이브러리

이번에는 최적의 방법으로 동선을 짜는 방법을 알아봤어요. 수학자들은 여러 개의 도시를 최소 비용으로 여행하는 방법, 일명 외판원 문제(TSP)를 연구한다는 소식을 들었거든요.

보통 가장 싸게 여행하고 싶어 하지요? 외판원 문제는 여러 도시 중 한 도시에서 다른 도시로 이동하는 비용을 모두 알고 있을 때, 최소 비용으로 모든 도시들을 한 번만 방문하고 시작점으로 돌아오는 경로를 구하는 문제입니다. 여기서 비용은 정하기 나름입니다. 총 이동거리여도 되고 경비여도 되지요.

언뜻 매우 쉬운 문제처럼 보여 많은 사람이 관심을 가졌습니다. 하지만 실상은 매우 어려워 이 문제에 뛰어든 수없이 많은 사람이 고난의 길을 걸었습니다. 

수학자들이 찾은 경로 문제 
 

경로 문제를 언제 처음으로 연구했는지는 불분명합니다. 현재까지 알려진 가장 오래된 기록은 아일랜드 수학자 윌리엄 해밀턴이 1856년에 만든 퍼즐입니다. 

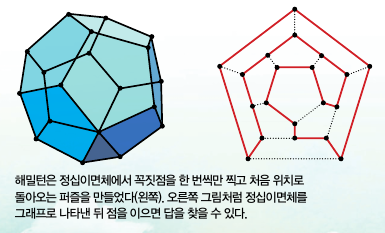
해밀턴은 정십이면체 위에 있는 꼭짓점 20개를 딱 한 번씩만 지나 출발점으로 되돌아와야 하는 퍼즐을 고안했습니다. 이 퍼즐은 보드게임으로 판매되다가 후대 사람들이 이런 종류의 문제에 해밀턴 이름을 붙여 학문적으로 연구하게 됐지요.  

모든 점을 한 번씩만 지나는 것을 ‘해밀턴 경로’, 여기서 다시 출발점으로 되돌아오는 것을 ‘해밀턴 회로’라고 하는데요, 한붓그리기와 헷갈리지 마세요! 해밀턴 회로가 점을 중복 없이 다 지나는 거라면 한붓그리기는 각 점을 잇는 길, 즉 변을 모두 지나는 문제입니다.

해밀턴 회로가 외판원 문제와 엮이는 이유는 도시를 점과 변으로 이뤄진 그래프로 표현하기 때문입니다. 정십이면체의 각 꼭짓점을 도시라 하면 외판원 문제가 되지요. 

실제 도시를 대입해 결과를 낸 첫 번째 연구는 1954년에 나왔습니다. 미국 랜드연구소 소속 수학자 3명이 미국의 49개 도시를 여행하는 최단 경로를 계산기로 계산해 구했지요. 사실 도시 수가 10개만 돼도 9!(약 30만) 가지가 넘는 왕복 경로가 있습니다. 도시가 15개면 8700억 가지가 넘지요. 그런데 일반 계산기로 계산했다니 정말 놀랍죠? 이후 랜드연구소는 더 많은 도시를 여행할 수 있는 경로를 짜는 사람에게 상금을 주겠다고 발표했습니다. 이를 계기로 여행하는 외판원 문제는 유명세를 탑니다.

앞서 말했지만 도시 수가 많아지면 경우의 수가 상상을 초월하기 때문에 아무리 컴퓨터를 이용한다고 해도 계산하는데 매우 긴 시간이 걸립니다. 계산을 조금 줄일 수 있는 방법이 없을까요? 우리는 ‘분기한정법’이라는 알고리듬을 찾았습니다. 이름은 어렵지만 원리는 간단합니다. 최적의 답이 될 만한 후보를 나무 가지처럼 늘어놓고 답이 될 가망이 없는 가지는 가차 없이 잘라버리는 방법이에요. 즉 답이 나올 수 있는 범위를 정해두고, 범위를 벗어나는 값들을 지워 계산의 양을 줄이는 거죠. 

외판원 문제는 모든 도시를 한 번씩은 반드시 다 들러야 하니, 모든 도시에서 딱 한 번씩 출발하고 한 번씩만 도착해야 합니다. 그래서 각 도시에서 다른 모든 도시로 이동할 때 나올 수 있는 비용 중, 최솟값들을 더하면 총 비용의 하한 값이 나옵니다. 

그렇다고 이 하한 값이 우리가 찾는 정답은 아니에요. 각 도시를 떠날 때 비용이 최소인 경로만 따라가다 보면 어떤 도시를 2번 이상 거칠 수도 있거든요. 하한 값은 그보다 더 짧은 여행 경로가 없다는 사실만 나타냅니다. 

이제 1회 이동을 시행했다고 가정합니다. 그러면 이 이동의 출발지와 도착지는 두 번 다시 출발지나 도착지가 될 수 없습니다. 또 이 이동의 비용은 앞서 구한 하한 값과 같거나 클 거예요. 따라서 이전 단계의 하한 값보다 다음 단계의 하한 값은 항상 크지요. 각 단계를 아래로 뻗는 나뭇가지로 나타낸다면(오른쪽 참고) 윗가지에 있는 하한 값은 무조건 아래 나올 가지의 하한 값보다 크거나 같습니다. 우선 하한 값이 작은 가지부터 계산해서 계산 시간을 줄이지요.