d라이브러리

김종락 교수의 보드게임 페스타는 이번 회를 마지막으로 연재를 종료합니다. 더 재밌는 연재로 찾아올게요!

바둑판과 바둑알로 꼭 바둑만 둘 수 있는 건 아닙니다. 규칙을 조금 바꾸면 오목도 둘 수 있고 알까기도 할 수 있지요. 오늘 소개할 ‘n-퀸즈 게임’은 체스의 규칙을 바꿔 만든 게임이에요.

체스는 체스판 위에서 폰과 룩, 비숍, 나이트, 킹, 퀸으로 즐기는 게임입니다. n-퀸즈 게임은 가로세로 n칸인 체스판과 서로 색이 다른 퀸 여러 개를 이용합니다. 퀸은 가로, 세로, 대각선 방향으로 몇 칸이든 움직일 수 있는 말이에요. 체스판과 체스 말이 없으면 바둑판과 바둑알을 이용해도 됩니다.

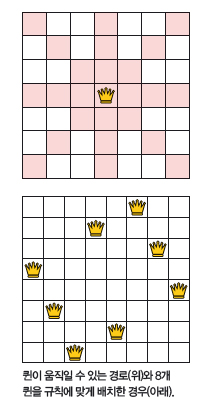
n-퀸즈 게임은 가로세로 8칸인 체스판 위에 퀸 8개를 규칙에 맞게 배치하는 ‘8-퀸즈 퍼즐’에서 시작됐습니다. 1848년 독일의 체스 문제 연구가인 막스 베젤이 처음 소개했고, 1850년 독일의 의사 프란츠 노크가 8-퀸즈 퍼즐의 해법을 알아내면서 가로세로가 n칸인 체스판 위에서 하는 퍼즐로 확장했지요. 이후 2016년 미국 베닝턴대학교 수학과 교수인 글렌 브러멜렌과 제자 하산 눈이 상대방과 겨루는 ‘게임’으로 만들었습니다.

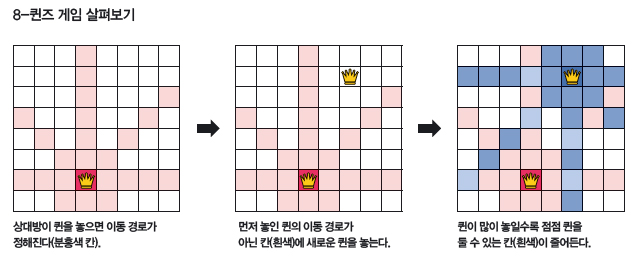
게임 방법은 서로 다른 색의 퀸을 가진 두 사람이 번갈아가며 체스판 위에 퀸을 하나씩 놓는 겁니다. 단, 규칙이 있습니다. 퀸들은 콧대가 높아서 자기가 움직일 수 있는 경로에 다른 퀸이 서 있는 걸 용납하지 않습니다. 심지어 색이 같아도 말이죠. 즉, 먼저 놓은 퀸을 포함한 행과 열, 대각선을 뺀 나머지 칸에만 퀸을 놓을 수 있고, 이렇게 게임을 진행하다가 자기 차례에 퀸을 놓을 곳이 없으면 지는 게임이지요.

항상 이길 수 있을까?

n-퀸즈 게임에서 퀸을 먼저 놓는 사람 또는 나중에 놓는 사람이 항상 이길 수 있는 방법이 있을까요? 만약 있다면, 퀸을 어디에 놓아야 이길 수 있을까요? 이 질문은 여러 수학자가 고민한 문제입니다.

아직 모든 자연수 n에 대해 n-퀸즈 게임에서 이기는 방법이 알려지지 않았지만, n이 홀수인 경우와 짝수 중 일부 경우에는 알려져 있습니다. 먼저 n=4인 4-퀸즈 게임에서 이기는 방법이 무엇인지 살펴보도록 하죠.

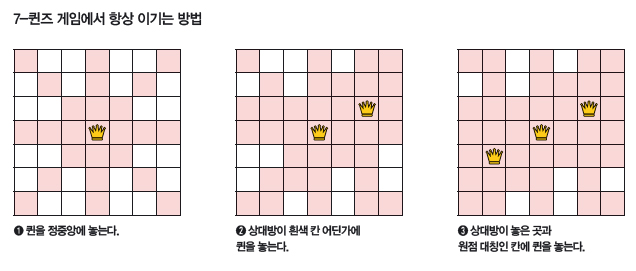
4-퀸즈 게임은 퀸을 먼저 놓는 사람이 항상 이길 수 있습니다. 처음 놓는 사람이 위 그림에서 왕관이 있는 칸에 퀸을 놓으면 상대방이 놓을 수 있는 곳은 흰색으로 표시된 4칸뿐입니다. 4칸 중 어디에 놓아도 1칸이 남는데, 처음 놓은 사람이 남은 1칸에 놓으면 상대방은 더는 놓을 곳이 없습니다. 따라서 처음 놓는 사람이 반드시 이기지요.

n이 홀수면 무조건 이긴다!

n이 짝수기만 하면 쓸 수 있는 ‘일반적인’ 방법이 있으면 더할 나위 없이 좋을 거예요. 하지만 n이
짝수인 n-퀸즈 게임에서 그런 방법은 알려지지 않았습니다. 반가운 소식은 n이 홀수인 n-퀸즈
게임에서는 먼저 놓는 사람이 항상 이길 수 있는 일반적인 방법이 있다는 겁니다. 바로 ‘원점 대
칭’을 이용하는 겁니다.

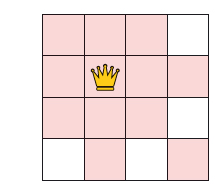
7-퀸즈 게임을 예로 들어보죠. 먼저 놓는 사람은 체스판 정중앙에 퀸을 놓습니다(❶). 상대방은 흰색 칸 어딘가에 퀸을 놓을 텐데(❷), 처음 놓는 사람은 정중앙을 좌표평면의 원점으로 생각한 뒤 상대방이 놓은 곳과 원점 대칭인 칸에 퀸을 놓습니다(❸). 이렇게 놓으면 먼저 놓은 퀸의 경로를 피하면서 동시에 홀수 번째 차례에 항상 퀸을 놓을 수 있으므로 게임에서 이길 수 있습니다.

모든 방법을 찾아라

상대방과 겨루는 ‘n-퀸즈 게임’과 달리 ‘n-퀸즈 퍼즐’은 가로세로 n칸인 체스판 위에 퀸 n개를 규
칙에 맞게 놓는 겁니다. n이 어떤 값이냐에 따라 놓는 방법이 없기도 하고, 많기도 합니다. n=27
인 경우엔 무려 234,907,967,154,122,528가지나 있지요.

n=2, n=3인 경우를 빼면 n 값과 관계없이 퀸 n개를 놓는 방법이 적어도 하나는 있습니다. ‘놓을
수 있다’는 것만 알 뿐 n 값에 따라 구체적으로 방법이 몇 가지인지 계산할 수 있는 공식을 모르
고, n이 무한히 커질 때 방법의 수가 수렴하는지 또는 발산하는지, 수렴하면 어떤 값으로 수렴하
는지도 모릅니다. 다만 n이 1~27일 때 방법의 수가 몇 개인지는 알려져 있어요.

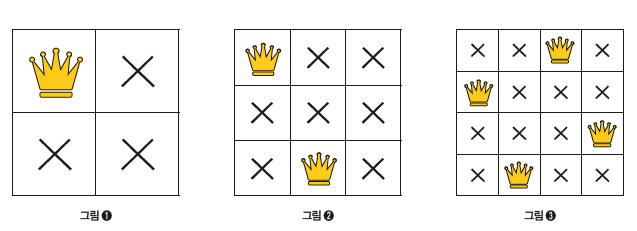
먼저 n=2인 경우, 퀸 2개를 놓아야 하는데 그림❶처럼 처음 놓는 사람이 퀸을 어디에 놓아도 다음 퀸을 놓을 곳이 없어서 퀸 2개를 놓는 게 불가능합니다. n=3인 경우는 어떨까요? 체스판을 돌리거나 뒤집어서 퀸의 위치가 같은 경우를 제외하면, 처음 놓는 사람이 퀸을 놓을 수 있는 곳은 구석, 변, 정중앙 3가지 경우밖에 없습니다. 먼저 정중앙에 퀸을 놓으면 더는 놓을 곳이 없고, 그림❷처럼 변과 구석에 놓는 경우 퀸을 2개만 놓아도 놓을 곳이 없어 불가능하지요.

n=4일 때부터는 가능합니다. 퀸 n개를 놓는 모든 방법을 찾아야 하는데, 하나하나 세지 말고 대칭
해도 겹치지 않는 방법들을 먼저 찾은 뒤, 대칭해서 다른경우만큼 더해주면 됩니다. 예를 들어 4-퀸즈 퍼즐은 그림❸과 같은 방법을 찾을 수 있습니다. 판을 좌우 또는 위아래로 뒤집었을 때 겹치는 모양을 한 가지로 치면 총 2가지 방법이 있지요. 이렇게 모든 방법을 찾을 때는 하나를 찾은 뒤, 대칭을 이용해 또 다른 방법을 찾아내는 게 요령입니다.

가우스도 관심 가진 8-퀸즈 퍼즐

8-퀸즈 퍼즐에 퀸 8개를 놓는 방법이 몇 개인지 처음 알아낸 사람은 수학의 황제 카를 프리드리히가우스입니다. 가우스는 컴퓨터도 없던 1850년에 방법이 총 92개라는 사실을 알아냈지요. 8-퀸즈퍼즐은 체스판의 칸이 총 64개이므로 모든 경우를 따지려면 총 64C8=4,426,165,368개를 따져야 합니다. 그래서 먼저 놓인 퀸이 속한 행과 열에 다음 퀸을 놓을 수 없다는 규칙에 따라 경우의 수를 줄입니다. 물론 대각선에도 놓을 수 없지만, 행과 열만 생각해도 많이 줄일 수 있어요.

체스판이 총 8개 열로 이뤄져 있으므로 첫 번째 칸에서 한 칸을 고르고, 두 번째 열에서는 앞서 선택한 칸을 뺀 7칸 중 한 칸을 고르면 앞서 놓인 퀸의 경로를 피할 수 있습니다. 결국 한 열에서 순서가 다르게 한 칸씩 고르는 것과 같으므로 8!=40,320개로 줄일 수 있는 거지요. 2002년 중국 베이징대학교 수학부의 종얀 큐는 대칭을 생각하지 않으면 아래와 같이 12가지 방법이 있다는 사실을 컴퓨터를 이용해 알아냈어요.

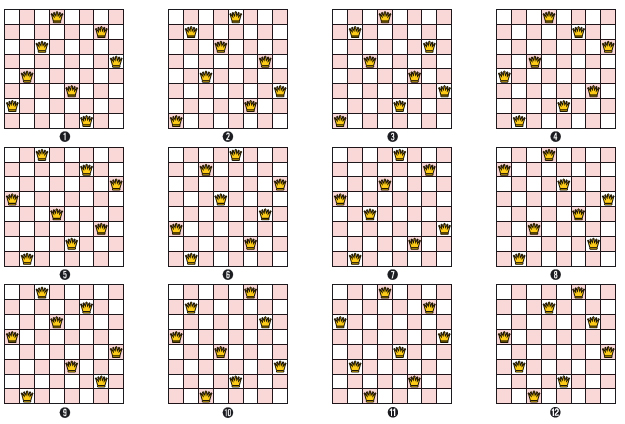
❶~ 번은 시계 방향으로 90°씩 회전하면 각각 다른 방법 3가지를 얻을 수 있고, 위아래, 좌우그리고 두 대각선으로 대칭 하면 각각 다른 방법 4가지를 얻을 수 있으므로 총 11×8=88가지 방법을 찾을 수 있습니다. 번은 다른 방법이 총 3가지 있으니까 결국 92가지의 서로 다른 방법이 있습니다. 여러분도 열심히 연구해서 n＞27인 경우엔 얼마나 많은 방법이 있는지 찾아보세요! 

김종락 서강대학교 수학과 교수는 포스텍 수학과를 졸업하고, 서울대학교에서 석사 학위, 미국 일리노이주립대학교 시카고캠퍼스에서 박사 학위를 받았습니다. 주요 연구 분야는 부호론과 암호론, 산업수학, 인공지능입니다. 2004년 캐나다 조합론연구소에서 주는 커크만 메달을 한국인 최초로 받았습니다. 2016년부터 대한수학회 수학문화 앰배서더로 활동 중이며, ‘감성수학레드’라는 스타트업을 운영하고 있습니다.