d라이브러리

‘도시 n개를 단 한 번만 방문하고 출발점으로 돌아 오려고 한다. 한 도시에서 다른 도시 사이의 거리가 모두 정해져 있을 때 최소 비용이 드는 이동 경로는 무엇일까?’

문제만 봐서는 안 어려워 보이지만 ‘최소 비용’이라는 말 때문에 외판원 문제를 해결하기가 매우 어렵습니다. 아주 좋은 경로를 하나 찾더라도 그보다 저렴한 경로가 없는지 확인해야 하는데, 이게 만만치 않거든요. 단순히 컴퓨터를 많이 쓴다고 될 일이 아닙니다. 도시 수가 42개만 돼도 따져야 할 경우의 수가 41×40×…×3×2×1로, 1049보다도 큽니다. 컴퓨터가 1초에 1억 개 경우를 처리한다고 해도 빅뱅으로 우주가 시작돼 현재까지 흐른 시간의 1023배 이상 걸리지요.

그래서 수학자와 컴퓨터과학자는 다양한 수학 기술을 동원해 문제를 풀고 있습니다. 첫 번째 의미 있는 결과는 1954년에 나왔습니다.

다양한 분야 전문가가 모여 연구하는 미국 랜드연구소 소속 세 명의 수학자 조지 댄치그와 레이 풀커슨, 셀마 존슨이 미국의 49개 도시를 최소 이동거리로 도는 방법을 일반 계산기로 찾았지요.

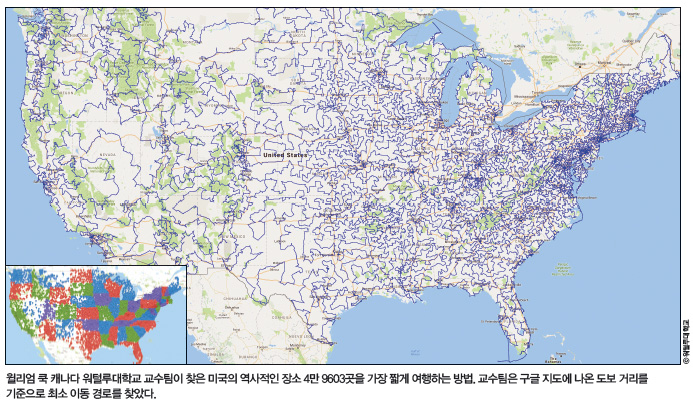
이후 학자들은 이 방법을 이용해서 최적의 답을 구할 수 있는 도시 수를 늘려갔습니다. 1977년에는 120개 도시, 1987년 2392개 도시에 관한 최적경로를 알아냈지요. 1998년에는 1만 3509개, 2004년에는 2만 4978개까지 늘렸습니다. 2006년 데이비드 애플게이트 AT&T연구소 박사가 이끄는 팀은 8만 5899개 도시에 대한 최적 경로를 계산하는 데 성공했지요.

최소 비용 찾는 건 불가능에 가깝다?

하지만 이 방법은 n개 도시를 여행하는 외판원 문제의 모든 경우를 효율적으로 해결하는 데 큰 도움이 되지 않습니다. 외판원 문제가 이론적으로 ‘NP-완전’이기 때문입니다. 애초에 최소 비용으로 여행할 수 있는 방법을 찾는 효율적인 알고리듬★이 존재하지 않을 수도 있지요.

효율적인 알고리듬★
입력하는 자료의 길이가 n자일 때, 답을 찾는 데 필요한 시간이 최대로 걸려도 n에 관한 다항식 이내로 걸리는 알고리듬.

미국 클레이연구소가 뽑은 7대 난제 중에 ‘P=NP’라는 추측이 있습니다. P는 정해진 단계 안에 풀리는 문제, NP는 문제의 풀이 과정을 보고 그 문제의 답이 옳은지 특정 횟수 안에 확인할 수 있는 문제를 말합니다. 그 중에서도 NP-완전은 NP 문제중에서 이 문제를 풀면 다른 NP 문제를 모두 특정 횟수 안에 풀 수 있다고 증명된 문제지요.

외판원 문제가 NP-완전이라는 사실은 1972년 미국 컴퓨터과학자 리처드 카프가 증명했습니다. 그런데 현재 많은 학자들이 P≠NP라고 생각합니다. 즉 외판원 문제를 푸는 효율적인 알고리듬은 없다는 거지요.

따라서 학자들은 근삿값을 찾는 연구를 하고 있습니다. 정답은 아니더라도 정답의 몇 배 이내의 값을 알려주는 알고리듬을 찾는 겁니다. 적당히 좋은 답에 만족하는 대신 계산을 훨씬 빠르게 할 수 있다면 그게 더 이득일 수도 있으니까요.

현재 두 도시를 여행할 때 어느 방향으로 가더라도, 즉 서울에서 부산을 가나, 부산에서 서울을 가나 비용이 같다면 정답의 1.5배 이내의 답을 찾아주는 효율적인 알고리듬이 알려져 있습니다. 이 알고리듬은 1976년 니코스 크리스토피드 영국임페리얼 칼리지 런던 교수가 찾았습니다. 알고리듬이 워낙 간단해서 대학 수업에서도 다룰 수 있지요.

하지만 1.5를 더 작은 수로 바꾸는 문제는 매우 어렵습니다. 한 동안 아무런 성과가 없었는데, 2011년 아민 세이버리 미국 스탠퍼드대학교 교수와 지도 학생인 샤안 오베이스 가람(현재 미국 워싱턴대학교 교수), 모힛 싱 미국 조지아공과대학교 교수가 이 1.5배를 1.44999999999999999999999999999999999999999999999999996으로 바꾸는 데 성공했지요. 연구팀은 1.5를 4/3까지 낮출 수 있을 거라고 추측했는데, 이마저도 매우 어려워 아직까지 풀리지 않았습니다.

5500을 얼마까지 줄일 수 있을까?

두 도시를 여행할 때 이동방향에 따라 비용이 다르게 든다면 어떨까요? 예를 들어 서울에서 뉴욕으로 가는 비행시간과 뉴욕에서 서울로 오는 비행 시간은 몇 시간씩 차이가 납니다. 자전거를 탈때도 오르막을 가면 느리지만, 반대로 내리막을 가면 빠르지요. 이 경우엔 크리스토피드 교수의 방법이 통하지 않아, 최근까지도 정답의 상수 배 이내의 답을 알려주는 알고리듬이 있기나 한 건지, 그 존재조차 미해결 문제였습니다.

그러던 2017년 8월, 올라 스벤손 스위스 로잔 연방공과대학교 교수와 지도 학생인 야쿠프 타르나프스키, 라슬로 베그흐 영국 런던정치경제대학교 교수가 이 문제를 해결한 39쪽짜리 논문을 인터넷에 공개했습니다. 정답의 5500배 이내의 답을 찾는 알고리듬을 찾은 겁니다. 정답인 비용이 1이라면 이 알고리듬은 항상 5500 이내의 비용이 드는 방법을 짧은 시간 안에 찾아줍니다. 앞으로 이 논문이 엄격한 검증을 거쳐 옳다고 판명 된다면, 기존 미해결 문제를 처음으로 해결한 논문으로 남을 겁니다.

그렇다면 5500을 어디까지 줄일 수 있을까요? 저 또한 매우 궁금한데요, 이제 이런 알고리듬이 가능하다는 것을 알았으니 상수를 낮추는 연구가 본격적으로 시작될 겁니다. 5500배 이내의 알고리듬이 당장 우리 생활에는 쓸모 없겠지만, 이 알고리듬 덕분에 나중에 탄생한 새로운 알고리듬이 우리 삶을 매우 편리하게 바꿔줄 수도 있습니다.