MC 유: 마침내 박사님 4명이 모두 모였어요. 이제 택시를 타고 근처에서 맛있다고 소문난 식당으로 이동해 본격적인 대화를 나눠 보도록 하죠! 그나저나 날도 더운데 택시는 왜 이렇게 안오는지…. 아휴 따분해!
MC 유: 과학 박사님, 왜 혼자서 싱글벙글 웃고 계신가요?
과학 박사: 하하. 답을 찾았어요! 저기 서 있는 택시 번호판의 답을 못 찾고 있었거든요.
MC 유: 답을 못 찾고 있었다니, 택시 번호판이 박사님께 문제라도 낸 건가요?
과학 박사: 번호판으로 계산 놀이를 하고 있었어요. 한 방송에서 밴드 페퍼톤스의 이장원 씨가 평소에 즐기는 놀이라고 소개한 걸 보고 저도 심심할 때마다 하고 있답니다. 규칙은 아주 간단해요. 네 자리의 자동차 등록 번호 사이에 사칙연산 기호를 알맞게 넣어서 계산한 결과가 자동차 종류 번호 두 자리와 같도록 만드는 거예요. 예를 들어 저 번호판은 ‘24나 1528’이니까 (1+5)÷2×8=24가 되죠.
MC 유: 박사님은 번호판에서도 수학을 찾으시는군요! 정말 심심할 겨를이 없겠어요.
과학 박사: 자동차는 흔하니까 지루할 때 한번 해보세요. 여러 가지 계산을 해보면서 사고력도 좋아지고, 정답을 찾아내면 꼭 택시 수를 발견한 ‘라마누잔’이 된 것 같은 느낌이 든다니까요.
잡학 박사: 인도의 수학자 스리니바사 라마누잔을 말하는 거죠? 가만 있자, 그 숫자가 1729였나…. 라마누잔이 병원에 입원했을 때, 병문안 온 영국 수학자 고드프리 하디가 타고 온 택시 번호를 듣고 두 가지 다른 세제곱의 합(13+123=93+103)으로 나타낼 수 있는 가장 작은 수라고 했다죠.

맥도날드에도 수학이!?
과학 박사: 참 재미있는 숫자지요. 택시 수처럼 이름이 붙은 수를 하나 더 소개해 드리죠. ‘행복 수’라고 해요. 어떤 자연수의 각 자릿수를 제곱해서 더하는 과정을 반복했을 때 1이 나오는 수예요. 예를 들어 44는 42+42=32 ⇨ 32+22=13 ⇨ 12+32=10 ⇨12+02=1을 거쳐 1이 되지요.
문학 박사: 저도 재미있는 수를 하나 알고 있어요. 자뻑이 심한 사람을 ‘나르시시즘’에 빠졌다고 하죠? 자연수 중에도 나르시시즘에 빠진 수가 있다고 해요. 각 자릿수를 세제곱해서 더했을 때 자기 자신이 나오는 수가 바로 ‘나르시시즘 수’예요. 나르시시즘 수를 찾는 게 생각보다 쉽지는 않습니다. 저는 딱 하나 알고 있네요. 153(=13+53+33)이요!
잡학 박사: 왠지 이 숫자가 더 나르시시즘이랑 어울리는 것 같아요. Emirp를 거울에 비춘 것처럼 거꾸로 읽어 보세요. Prime(소수)이 되죠? Emirp는 거꾸로 읽어도 소수인 수를 뜻해요. 13, 17, 37, 113 같은 수가 바로 Emirp죠.
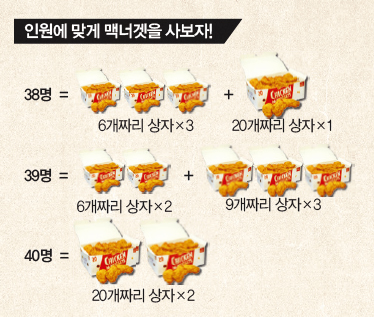
미식 박사: 저는 음식 전문가니까 저기 보이는 맥도날드와 관련 있는 수를 말해볼게요. 다들 ‘맥너겟’을 먹어 본 적 있죠? 맥너겟은 6, 9, 20개 세 종류의 상자로만 파는데 6, 9, 20 세 수를 여러 번 더해서 만들 수 있는 수를 ‘맥너겟 수’라고 해요. 1, 2, 3, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 22, 23, 25, 28, 31, 34, 37, 43을 제외한 모든 자연수가 전부 맥너겟 수가 된답니다. 그러니까 맥너겟을 여러 상자 사려는데 필요한 개수가 저 숫자 중 하나면 무조건 몇 개는 남거나 모자르다는 거죠!
과학 박사: 역시 박사님들, 재미있는 수를 많이 알고 계시네요! 이렇게 정수의 재미있는 성질을 찾는 활동을 ‘유희수론’이라고 불러요. ‘읽고 쓰기 수열’로 유명한 존 콘웨이라는 수학자는 이런 규칙을 연구해서 논문을 쓰기도 했고, 닐 슬론이라는 수학자는 이런 수를 모아 수열 사전을 만들기도 했어요. 단순히 재미로 한다고 하지만, 이런 활동이 모두 정수의 성질을 밝히는 활동이니 나름의 새로운 규칙을 찾아보는 것도 좋을 거예요. 혹시 알아요? 나중에 엄청난 연구로 이어질 수도 있어요.
MC 유: 박사님들 말씀을 들으니 주변에 있는 숫자가 전부 수학 문제처럼 보이는군요. 제가 수포자였다는 사실을 들킬까 봐 조마조마했는데 벌써 걱정입니다. 앗, 잠깐 택시 기사님, 여기 탈 사람 있어요!

▼관련기사를 계속 보시려면?











