d라이브러리

“어제 왕자님이 잠든 뒤 복제 실험을 시작했습니다.”

방문을 열고 들어온 복제 전문가의 말에 로봇 왕자는 졸음이 확 달아났습니다.

“이제 성 바깥으로 나갈 수 있는 거군요! 야호!”

흥분한 왕자와 달리 복제 전문가는 침착하게 말을 이었습니다.

“어젯밤, 왕자님이 잠든 뒤 저는 주사위를 던졌습니다. 홀수 눈이 나오면 왕자님을 복제하지 않고 아침에 그대로 깨울 것이요. 짝수 눈이 나오면 왕자님의 몸과 마음과 기억을 그대로 복제해 왕자님을 하나 더 만들기로 했습니다. 그리고 아침이 되면 진짜 왕자님이든 복제된 가짜 왕자님이든 모두 깨우기로 했습니다. 지금이 바로 그 아침입니다.”

왕자는 복제 전문가의 말을 듣는 둥 마는 둥 했습니다. 한시라도 빨리 성을 탈출하고 싶은 마음이 컸지요.

“왕자님, 하지만 저는 왕자님이 진짜 왕자님인지, 가짜 왕자님인지 말씀드릴 수 없습니다. 다른 방에 왕자님이 있는지 없는지 말씀드릴 수 없지만, 있다면 그 분께도 똑같이 말씀드렸어요.”

왕자는 혼란스러웠습니다. 자신과 모든 것이 똑같은 왕자가 한 명 더 있어도 누가 진짜이고 누가 가짜인지 증명할 방법이 없다는 것을 깨달았기 때문입니다. 뿐만 아니라 스스로 진짜 왕자인지 가짜 왕자인지도 모르는 미궁에 빠진 셈입니다. 모든 것을 알고 있는 복제 전문가는 문제 하나를 남기고 그 길로 성을 떠나버렸습니다. 왕자는 방에 갇힌 채 고민에 빠졌습니다.

자아를 잃은 왕자의 확률 계산

잠에서 깨어나 자신의 정체마저 헷갈리는 왕자는 복제 전문가가 던진 주사위가 홀수 눈이 나왔을 확률을 구해야 합니다. 왕자는 답을 구하기 위해 조금 더 간단한 실험을 먼저 생각해 보기로 했습니다.


 1단계  반드시 진짜 왕자가 깨어나는 실험
일요일 밤에 진짜 왕자가 잠든 사이 복제 전문가가 진짜 왕자를 똑같이 복제해 가짜 왕자를 만든다고 가정합시다. 그리고 주사위를 던져 홀수 눈이 나오면 월요일 아침에 진짜 왕자만 깨우는 실험을 ‘실험 A’라고 하겠습니다. 짝수 눈이 나오면 두 왕자를 모두 깨우는 조건은 실험 A에서도 유효합니다.

실험 A와 복제 전문가가 제안한 실험은 아주 비슷합니다. 실험 A에서는 가짜 왕자를 만들되 주사위가 홀수 눈이 나왔을 때 깨우지 않고 계속 자도록 둡니다. 복제 전문가의 실험에서는 주사위가 홀수 눈이 나오면 가짜 왕자를 만들지 않을 뿐입니다.

그러므로 깨어난 왕자가 뭐라고 답할지는 몰라도 실험 A에서 깨어난 왕자가 구한 ‘일요일에 던진 주사위가 홀수 눈이 나왔을 확률’은 복제 전문가가 제안한 실험에서 깨어난 왕자가 구한 확률과 같다고 추측할 수 있습니다.

 2단계  반드시 가짜 왕자가 깨어나는 실험
이번에는 ‘실험 B’를 생각해 보겠습니다. 모든 조건은 실험 A와 같되 주사위의 눈이 홀수가 나오면 월요일 아침에 반드시 가짜 왕자만 깨우는 실험입니다.

이때 실험 A에서 깨어난 왕자의 답이 뭔지는 알 수 없어도 그 답이 실험 B에서 깨어난 왕자의 답과 같을 것임을 알 수 있습니다. 실험 A와 실험 B 두 경우 모두 주사위의 눈이 홀수가 나왔을 때는 한 사람만 깨어나고, 짝수가 나왔을 때는 두 사람이 깨어나기 때문입니다. 깨어난 사람이 진짜 왕자인지 가짜 왕자인지가 유일한 차이점인데, 이 사실은 깨어난 왕자의 답을 바꾸지 못 합니다.

 3단계 ➊  두 실험을 합친 마구잡이 실험
2단계에서 실험 A의 ‘진짜 왕자가 잠에서 깨어나 구한 확률’이나 실험 B의 ‘가짜 왕자가 잠에서 깨어나 구한 확률’은 같다는 결과가 나왔습니다. 그러므로 이 확률이 무엇인지는 모르지만, 일요일 밤에 왕자를 복제한 뒤에 주사위를 던져 홀수 눈이 나오면 둘 중에 한 명을 마구잡이로 골라 깨우는 실험에서도 같은 확률이 나올 것입니다.

이 실험을 ‘마구잡이 실험’이라고 부르겠습니다. 즉, 마구잡이 실험에서 깨어난 왕자의 답이 복제 전문가가 제안한 실험에서 깨어난 왕자의 답입니다. 그렇다면 마구잡이 실험에서 깨어난 왕자의 답은 무엇이어야 할까요? 아래를 보세요.

 

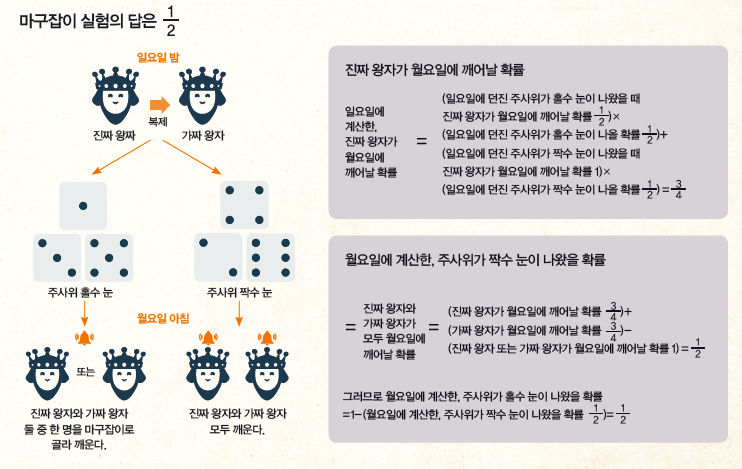
왕자는 자아를 찾을 수 있을까
계산에 따라 마구잡이 실험에서 잠에서 깬 왕자의 답은 1/2이어야 합니다. 왕자는 답이 1/2이라고 확신했지요. 그러자 복제 전문가가 나타나 지난 화에서 이야기한 두 공주의 실험을 언급했습니다. 동전이 앞면이 나오면 큰 공주와 작은 공주 둘 중 한 명을 골라 깨우고, 뒷면이 나오면 큰 공주와 작은 공주 모두를 깨워 ‘일요일에 던진 동전이 앞면이 나왔을 확률’을 묻는 실험이었습니다.

“두 공주의 실험은 마구잡이 실험과 무척 비슷합니다. 그런데 두 공주의 실험에서 공주는 일요일에 던진 동전이 앞면이 나왔을 확률이 1/3이라고 주장했습니다. 똑같은 논리로 마구잡이 실험에서도 주사위가 홀수 눈이 나왔을 확률이 1/3이라고 주장할 수 있습니다. 왕자님의 답 1/2이 맞다고 확신할 수 있습니까?”

의미심장한 말을 남긴 채 복제 전문가는 또 다시 사라졌습니다. 이제 결정은 독자의 몫으로 남았습니다.


다음 이야기
보물이 든 상자 하나와 빈 상자 두 개가 있습니다. 사라는 각 상자 안에 무엇이 들었는지 알고 있습니다. 상자 안에 무엇이 들어있는지 모르는 우리는 세 상자 가운데 하나를 골라야 합니다. 우리가 고른 상자에 보물이 들어 있을 확률은 1/3 입니다.

우리가 상자를 고르면 사라는 빈 상자를 하나 열어 보여줍니다. 이제 우리가 고른 상자에 보물이 들어 있을 확률은 얼마일까요? 그리고 보물이 든 상자 하나와 빈 상자 세 개로 게임을 한다면 우리가 고른 상자에 보물이 들어 있을 확률은 얼마일까요? 우리가 고른 상자를 제외한 상자 중 사라가 빈 상자를 하나 열어 보여준다는 조건은 같습니다.

당신의 선택
학교를 졸업한 어른도 논리적으로 생각하기는 쉽지 않다. 과연 복제된 왕자에 관한 문제를 접한 어른들은 왕자의 답이 무엇이라고 답할까? 지난 3월 11일에 논리적인 표현을 공부하는 어른들의 모임 ‘두뇌보완계획’을 찾아가 의견을 들었다.