d라이브러리

Prologue_ 영국인인 레뮤엘 걸리버는 어린 시절부터 자신이 언젠가는 세계를 여행하게 될거라고 믿고 있었습니다. 마침내 어른이 된 걸리버는 의사 자격으로 배를 타고 머나먼 땅으로 항해를 떠납니다. 그런데 걸리버가 탄 배가 암초에 부딪쳐 산산조각이 나고 맙니다. 바다를 표류하던 걸리버는 이 때부터 기이한 세계를 떠돌며 믿기 어려운 모험을 겪게 되는데….

몸이 커지면 먹는 양은 몇 배?
 

 마지막으로, ‘산 같은 사람’은 위의 모든 조항을 준수하겠다는 선서에 따라 하루에 국민들 1천 728명을 먹이기에 충분한 분량의 고기와 마실 것을 지급받게 될 것이고, 릴리퍼트의 국왕을 자유로이 만나볼 수 있으며, 그 외의 다른 호의도 받을 것이다.
...(중략)

 독자들은 내가 자유를 회복할 수 있는 마지막 조항에서 국왕이 작은 사람들 1천 728명을 먹여살릴 만큼 충분한 양의 고기와 마실 것을 나에게 지급하겠다는 대목에 주의해 주기를 바란다. 나중에 한 친구에게 어떻게 그렇게 해서 그처럼 분명한 숫자에 도달할 수 있었는가를 물었다.

 정신을 차린 걸리버는 키가 12~13cm밖에 되지 않는 작은 사람들에 둘러싸여 있다는 사실을 깨닫습니다. 그 곳은 작은 인간들이 사는 소인국 릴리퍼트였던 것이죠. 몇 차례 위기도 겪지만 걸리버는 소인국 사람들을 도와 주면서 릴리퍼트의 국왕에게 인정을 받습니다. 릴리퍼트의 국왕과 걸리버가 맺은 조약 중에는 위처럼 릴리퍼트는 걸리버에게 1728명을 먹일 수 있는 음식을 제공한다는 항목이 있습니다. 왜 1700이나 1800이 아니라 꼭 1728명일까요?

그건 측정 결과 걸리버의 키가 릴리퍼트의 사람보다 약 12배 컸기 때문입니다. 길이가 12배 커지면 면적은 12의 제곱, 부피는 12의 세제곱만큼 커집니다. 간단히 선분과 사각형, 정육면체를 예로 들어 보지요.

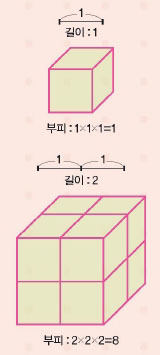
길이가 1인 선분을 한 변으로 하는 정사각형과 정육면체를 각각 만들어 봅시다. 그러면 정사각형의 넓이는 1의 제곱인 1, 정육면체의 부피는 1의 세제곱인 1이 됩니다. 한편 길이가 12인 선분을 한 변으로 하는 정사각형과 정육면체를 만들었을 때는 어떨까요? 정사각형의 넓이는 12의 제곱인 144, 정육면체의 부피는 12의 세제곱인 1728이 됩니다.

걸리버의 키가 소인보다 12배 크다고 한 것은 당시 영국에서 12진법을 많이 쓰고 있었기 때문입니다. 12진법은 아직 영국에서 쓰는 단위에 흔적이 남아 있지요. 예를 들어, 1피트(약 30cm)는 12인치(약 2.54cm)랍니다.

거인의 음악은 너무 시끄러워?
 

음악을 좋아하는 국왕은 자주 연주회를 열었다. 가끔씩 나도 초청을 받았다. 탁자 위에 상자를 올려놓고 음악을 들었다. 음악소리가 너무나 컸기 때문에 음정을 거의 구별할 수가 없었다. 육군 군악대의 북과 나팔이 동시에 독자들의 귀 앞에서 소리를 내더라도, 내가 브롭딩낵에서 들은 음악과 비교 할 수는 없을 것이다. 

나는 연주자들이 앉아 있는 곳에서 최대한 멀리 상자를 놓아 달라고 부탁했다. 그리고 문과 창을 닫고 커튼을 내렸다. 그렇게 하고나서 들으니까 그 나라의 음악도 듣기 좋은 것이었다.

소인국을 떠나 무사히 집으로 돌아간 걸리버는 얼마 뒤 다시 배를 타고 여행을 떠납니다. 그리고 또 사고에 휘말려 거인들이 살고 있는 브롭딩낵에 도착합니다. 브롭딩낵은 릴리퍼트와 달리 거인들이 살고 있는 나라입니다. 거인들의 손아귀에 들어갈 정도로 작은 걸리버는 브롭딩낵의 음악 소리가 너무 커서 잘 들을 수 없다고 불평합니다. 그런데 과연 거인들의 악기에서 나는 소리가 크기만 할까요?
 

케플러의 제 3법칙

그들은 화성의 주위를 돌고 있는 두 개의 위성을 발견하였다. 안쪽에 있는 위성은 화성의 중심으로부터 직경의 세 배되는 거리에서 돌고 있었으며, 밖에 있는 것은 직경의 다섯 배 되는 거리에서 돌고 있었다. 한 바퀴 도는 데 걸리는 시간은, 안에 있는 위성이 열 시간, 밖에 있는 위성이 스물 한 시간 삼십 분이었다. 따라서 운행시간의 제곱은 화성의 중심으로부터 거리의 세제곱에 비례하는 것이다.

브롭딩낵을 떠난 걸리버가 다음에 도착한 나라는 공중을 떠다니는 도시 라퓨타입니다. 라퓨타는 수학이 굉장히 발달한 나라로, 식사를 할 때도 빵을 원뿔이나 평행사변형 등 수학적인 도형 모양으로 잘라 먹는 곳이죠. 또한 훌륭한 망원경을 가지고 있어 천체를 관측하는 일에 삶의 대부분을 보냅니다.

걸리버는 이 곳의 학자들에게서 수학과 천문학에 대해 많은 이야기를 듣습니다. 그 중에는 라퓨타의 학자들이 발견한 화성의 두 위성에 대한 이야기도 있습니다. 걸리버는 이 두 위성의 공전주기의 제곱과 화성으로부터의 거리의 세제곱이 비례한다고 기록하고 있지요.
 

자동 글쓰기 기계
 

그 종이 위에는 그 나라 말의 모든 단어와 문법, 시제, 격변화가 무질서하게 적혀 있었다. 교수는 기계를 움직일 테니 자세히 관찰해 보라고 하였다.

그의 지시에 따라 학생들은 액자의 주위에 붙어 있는 40여 개의 손잡이를 돌렸다. 단어의 배열이 완전히 바뀌어졌다. 그러자 그는 36명의 학생들에게 액자에 나타난 몇 개의 문장을 조용히 읽으라고하였다. 그들은 액자에서 한 문장을 만들 수 있는 서너 개의 단어를 찾아서 나머지 네 명의 학생에게 받아 쓰도록 하였다. 이 작업이 서너 차례 반복되었다. 기계를 돌릴 때마다 정방형 나무 조각들이 뒤집히면서 단어들이 새로운 곳에 들어가도록 만들어져 있었다.
(중략)

교수는 그 문장들을 서로 묶을 생각을 하고 있었다. 이 풍부한 자료로부터 그는 학문과 과학에 대한 완전한 체계를 만들어 세상 사람들에게 제공하겠다는 것이다.

라퓨타의 여러 학자들과 이야기를 나누어 본 걸리버는 특이한 학자 한 명을 만납니다. 바로 액자와 같은 기계로 단어를 조합해 문장을 만드는 일을 하는 언어학자입니다. 이 액자에는 그가 아는 모든 단어가 들어 있는 것은 물론 명사와 동사가 쓰이는 비율도 담겨 있다고 합니다. 그는 이런 액자 500개를 설치해 문장을 수집한다면 온 세상의 학문과 과학을 총정리할 수 있다고 주장합니다. 걸리버는 이 훌륭한 기계에 대해 찬사를 아끼지 않으며 고국으로 돌아갈 때 이 기계의 설계도를 가지고 가게 해 달라고 부탁합니다.

이 언어학자의 꿈은 실현될 수 있을까요? 수학적으로 따져 봅시다. 이 액자는 ‘경우의 수’를 구하는 문제와 관련이 있습니다.

하나의 문장은 기본적으로 명사, 형용사, 부사, 동사 등의 단어로 이루어집니다. 여기에 과거형, 미래형, 존댓말 등의 변화가 적용되면 더욱 복잡해지지요. 먼저 ‘밥을 먹는다’와 같이 명사와 동사만으로 이루어진 가장 간단한 문장을 생각해 볼까요? 100개의 명사와 100개의 동사가 있을 경우 1개의 명사와 조합할 수 있는 동사의 수는 100개입니다. 따라서 100개의 명사와 100개의 동사를 조합해 만들 수 있는 문장의 수는 100×100인 10000가지입니다.
 

바구니 빨리 슬프다?

걸리버가 그린 액자를 보면 가로, 세로 각각 16개의 칸이 있습니다. 따라서 액자에는 총 256칸이 있고 손잡이를 한 번 돌릴 때마다 256가지의 서로 다른 단어가 나타납니다. 이 단어 중 명사, 동사, 형용사, 부사 등의 단어가 각각 몇 개인지는 정확히 쓰여 있지는 않지만 조합의 개수가 각각의 곱셈으로 나타난다는 점을 고려해 보면 수십만 개의 문장을 조합할 수 있음을 알 수 있습니다. 예를 들어, 명사가 50개, 부사가 100개, 동사가 100개일 경우 50×100×100=500000이므로 50만 가지의 문장을 만들 수 있습니다.

물론 50만 가지의 문장 중 대다수는 의미가 없는 엉뚱한 문장일 가능성이 큽니다. “바구니 빨리 슬프다”처럼 말이지요. 이 중에서 책에 쓸 수 있을 만큼 의미 있는 문장을 찾아 내는 건 결국 사람이 해야 할 몫입니다. 수십, 수백만 개의 문장에서 의미 있는 문장을 골라 내는 일이라니 시간이 엄청나게 오래 걸리겠지요? 걸리버가 만난 언어학자가 과연 살아생전에 꿈을 이루어 낼 수 있을지 모르겠습니다.

Epilogue_걸리버는 공중도시 라퓨타를 떠난 이후 고상하고 예의 바른 말들이 사는 휴이넘의 나라를 거쳐 마침내 집으로 돌아옵니다. 그리고 장장 16년 7개월에 걸친 여행기를 자세히 기록해 발표했지요. 걸리버의 여행기는 사람들에게 미지의 세상과 그 안에 숨은 재미있는 원리에대해 알려 주었답니다.