
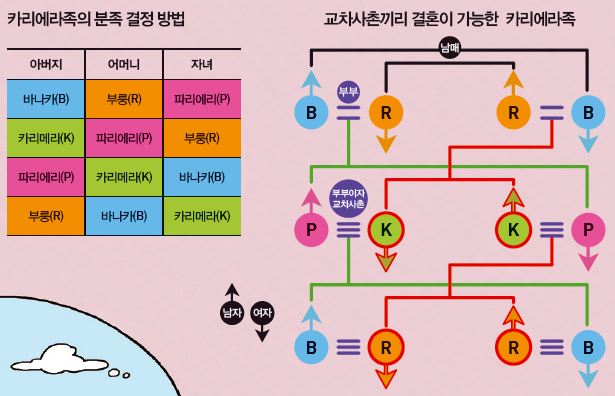
겉보기에 원주민 사회는 하나의 부족으로 이뤄진 것처럼 보이지만, 그 안을 자세히 살펴 보면 여러 개의 분족으로 나뉘어 있다. 인구가 750명 정도인 카리에라족은 바나카와 부룽, 카리메라, 파리에리라는 4개의 분족으로 이뤄졌다. 카리에라족이라면 누구나 이 4개의 분족 중 하나에 속한다. 그리고 자신이 속한 분족에 따라 결혼 상대의 분족이 정해진다. 즉 결혼은 바나카족과 부룽족이 하거나 아니면 카리메라족과 파리에리족이 해야 한다.
그리고 이들 사이에서 태어난 자녀는 아버지가 바나카족이면 파리에리족, 카리메라족이면 부룽족, 파리에리족이면 바나카족, 부룽족이면 카리메라족이 됐다. 이런 독특한 규칙은 다른 나라 혹은 다른 원주민 부족에서 찾아 볼 수 없다.
프랑스의 유명한 인류학자 클로드 레비스트로스는 이들이 왜 특정 부족 사람하고만 결혼해야 하는지, 자식은 왜 부모의 분족을 따르지 않는지를 설명하려고 했다. 하지만 이 문제를 깊게 고민할수록 수학자의 도움이 절실히 필요하다는 것을 느꼈다. 결국 당시 프랑스에서 이름을 떨친 수학 집단 부르바키에게 도움을 요청했다.
평행사촌끼리의 결혼은 안돼!
그 결과 1949년 부르바키의 공동 창립자인 프랑스의 수학자 앙드레 베유가 그 해답을 내놓았다. 바로 카리에라족의 결혼제도가 ‘클라인 4원군’(35쪽 참조)을 따랐던 것이다. 이는 궁극적으로 ‘평행사촌’끼리의 결혼을 피하기 위해서였다. 즉 삼촌의 아들과 딸이나 이모의 아들과 딸처럼 ‘아버지의 형제’나 ‘어머니의 자매’의 자녀와 결혼하는 것을 막아 준다. 하지만 부모와 성별이 다른 형제자매의 자녀(교차사촌)인 고종사촌이나 외사촌과는 결혼할 수 있다.
사촌과의 결혼이라 우리에게는 조금 생소하다. 우리나라에서는 8촌 이내의 친척은 서로 결혼하지 못하게 법으로 막고 있다. 우리나라뿐 아니라 중국과 대만 등 많은 동아시아 나라에서도 가까운 친척 사이의 결혼을 금지하고 있다. 대체 왜 그러는 걸까?
여러 가지 이유가 있지만 과학적으로 설명하면 열성 유전의 위험성 때문이다. 열성 유전병 유전자가 남매 사이의 결혼에서는 4명 중 1명, 8촌 사이에서는 125명 중 1명, 14촌 사이에서는 1만 6000명 중 1명, 16촌 사이에서는 6만 5000명 중 1명꼴로 나타난다. 먼 친척일수록, 즉 남남일수록 확률이 크게 낮아진다.
물론 열성 유전병 유전자를 갖고 있다고 해서 바로 다음 세대에 큰 영향을 주는 것은 아니다. 하지만 이 유전자를 가진 사람끼리 여러 세대에 걸쳐 반복적으로 결혼해서 자식을 낳으면 유전병을 걱정할 만큼 위험성이 커진다. 그래서 미국 메인주에서는 의사에게 유전자 상담을 받은 확인서를 가지고 와야 친척 사이의 결혼을 허락한다.
결혼한 사람과 백년해로할 가능성은?
결혼에 막 골인한 신혼부부가 앞으로 백년해로할 가능성은 얼마나 될까? 지난 2009년 옥스퍼드대와 워싱턴대 공동연구팀이 부부가 행복하게 함께 살 기간을 예측하는 공식을 개발했다.
연구팀은 갓 결혼한 신혼부부 700쌍에게 돈과 사랑 등 다양한 주제에 대해 각각 15분간 토론하게 했다. 그리고 이를 녹화한 뒤 개개인이 한 말을 숫자로 나타냈다. 배우자의 의견을 존중하거나 애정이 담긴 말을 하면 플러스 점수를, 분노에 찬 말을 하면 마이너스 점수를 줬다. 사용하는 단어에 따라 +4점에서 -4점까지 점수를 매겼다.
예를 들어 상대방에게 ‘멍청이’라고 말하면 -4점을 주고, ‘사랑해’라고 말하면 +4을 줬다. 이렇게 수치화한 자료를 개개인 별로 그래프로 만든 뒤 패턴을 분석해 이 부부가 몇 년간 결혼생활을 유지할 수 있는지 예측하는 방정식을 만들었다. 그리고 이 방정식이 얼마나 정확한지 확인하기 위해 12년 동안 매 1~2년마다 이들 부부에게 연락해 이혼 여부를 물었다. 그 결과 방정식으로 예측했던 결과와 94% 가량 들어맞았다.
연구팀에 따르면 백년해로할 가능성이 높은 부부는 서로의 말에 귀를 기울이고 서로의 장점에 관심을 갖는 부부다. 어떤 신혼부부는 지금 당장 이혼하는 게 더 낫다는 결과가 나오기도 했다. 연구팀은 상대방을 저주하는 표현을 많이 한 경우라고 밝혔다.
클라인 4원군 파헤치기!
클라인 4원군이란 독일의 수학자 펠릭스 클라인이 1884년 고안한 군으로, 4개의 원소가 이루는 군이다. 대표적인 예로는 두 변환을 연속해서 수행하는 연산 ★에 대한 집합 A={p, q, r, e}를 들 수 있다.
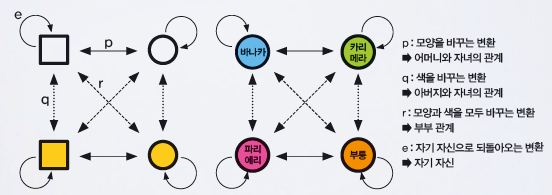
놀랍게도 집합 A에 카리에라족의 결혼제도를 대입하면 일치한다. 먼저 사각형과 원을 각각 바나카족과 카리메라족으로, 색칠된 사각형과 원을 각각 파리에리족과 부룽족으로 바꾼다. 그리고 p를 어머니와 자녀의 관계, q를 아버지와 자녀의 관계, r를 부부 관계, e를 자기 자신이라고 정한다. 예를 들어 바나카족 남자와 부룽족 여자가 결혼하면(r), 자식은 파리에리족이다. 바나카족 아버지와 파리에리족 자녀의 관계(q)와 부룽족 어머니와 파리에리족 자녀의 관계(p)가 성립한다.
카리에라족의 결혼제도로 보는 군의 정의
집합 A와 연산 ★이 있을 때 아래의 조건을 모두 만족하면 군이라 한다.
❶ 연산 ★에 대해 집합 A는 닫혀 있다.
⇒p★p=e∈A, p★q=r∈A, p★r=q∈A, p★e=p∈A, q★p=r∈A, q★q=e∈A, q★r=p∈A, q★e=q∈A, r★p=q∈A, r★q=p∈A, r★r=e∈A, r★e=r∈A, e★p=p∈A, e★q=q∈A, e★r=r∈A, e★e=e∈A이므로, 연산 ★에 대해 집합 A는 닫혀 있다.
❷ 연산 ★에 대해 결합법칙이 성립한다.
⇒(p★q)★r=r★r=e, p★(q★r)=p★p=e이므로, 연산 ★에 대해 집합 A는 결합법칙이 성립한다.
❸ 연산 ★에 대해 항등원이 존재한다. 항등원이란 어떤 원소에 연산을 해도 그 원소가 되는 원소다.
⇒p★e=p이므로, 항등원이 존재한다.
❹ 연산 ★에 대해 역원이 존재한다. 역원이란 어떤 원소에 연산을 했을 때 항등원이 되는 원소다.
⇒p★x=e인 x=p가 유일하게 존재하므로, 역원이 존재한다.
집합 A는 이 조건을 모두 만족하므로 연산 ★에 대해 군이다. 특별히 여기서는 클라인 4원군이다.
▼관련기사를 계속 보시려면?
Intro 수학은 안다 가족끼리 왜이래
Part 1 전통의 빅데이터, 족보
Part 2 수학이 만든 “결혼의 법칙”
Part 3 엄마 핏줄이 더 당긴다?!











