d라이브러리

거짓말할 때마다 코가 늘어나는 피노키오와 발 대신 램프와 연결된 꼬리(?)로 원하는 것은 다 만드는램프의 요정 지니. 애니메이션 속에 등장하는 두 캐릭터의 공통점은 바로 몸의 일부를 자유롭게 늘리거나 줄일 수 있다는 점이다. 물론 우리가 살고 있는 세상에서는 불가능한 일이지만, 만약 가능하다면 어떤 일들이 일어날까?

초능력자 엄마, 알고 보니 고무인간?!
 

이런 유쾌한 상상이 애니메이션으로 태어났다.‘100% 인간 캐릭터와 100개가 넘는 세트! 100점 만점의 최첨단 기술의 결정판!’이라는 화려한 수식어가 달린 애니메이션‘인크레더블’이 그 주인공이다.

평범해 보이는 한 가족이 등장한다. 하지만 이들 가족구성원은 모두 각자 다른 초능력을 지닌 특별한사람들. 무의식중에도 특별한 능력이 발휘돼 이들의 일상은 하루도 조용할 날이 없다.

그러던 어느 날, 악당‘인크레디 보이’가 인크레더블을 어려움에 빠뜨린다. 자기가 세상을 지배하는슈퍼영웅이 되겠단다. 이런!‘아빠가 위험하다’는 사실을 안 가족, 드디어 출동이다!

출동하기 전에 각자 어떤 초능력을 가지고 있는지 살펴보자. 누군가 위험에 빠지면 어디선가 눈썹이 휘날리게 날아와 깔끔하게 일을 처리하는 아빠 인크레더블, 팔다리가 자유자재로 쭉쭉 늘어나는 고무줄 몸매 엄마‘일라스티 걸’, 종종 투명인간이 되기도 하고 공격 받을 때면 포스필드라는 방어막을 만들어 자신을 보호하는 첫째 딸‘바이올렛’, 번개같이 빠른 발을 가진 질주본능 둘째 아들‘대쉬’,자신의 몸을 원하는 모양으로 만들 수 있는 변신돌이 막내‘잭잭’까지 인간의 상상력의 끝을 엿볼 수 있다. 만약 이 애니메이션에서 하나의 초능력만을 중심으로 내용을 전개했더라면 이만큼 큰 인기는 얻지 못했으리라.

이 중에서도 오늘은 고무줄처럼 늘어나는 엄마와 막내 잭잭의 초능력에 집중해보자. 그녀의 팔다리는마치 고무줄로 된 것 같아 때에 따라 길이를 줄여 악당의 눈을 피하거나, 몸을 늘려 낙하산으로 만들기도 한다. 또한 아이들이 위험에 처하면 자신의 몸을 배 모양으로 만들어 물 위에 띄우고 강을 건넌다. 잭잭은 마냥 아기처럼 보이지만 위험에 처하면 악마 등 다양한 모습으로 변신해 위기를 면한다.

변신의 비밀은 수학!
 

애니메이션‘인크레더블’속 엄마(일라스티 걸)와 영화‘마스크’의 주인공인 마스크(짐 캐리 역)는 너무나 자연스럽게 자신의 신체를 늘리고 줄인다. 이 같은 변신은 영화를 만드는 컴퓨터 그래픽 기법의 일부인 와핑과 모핑 기법을 이용한 것이다. 분명 이와 관련된 용어는 처음 접하는 독자들도 있을 터, 하나씩 차근차근 살펴보자.

‘와핑(warping)’은 원래의 모습은 그대로 두고 일부만 변형하는 기술이다. 물체의 구조나 질감은 그대로 두고 모습의 일부만 바꿀 때 쓰인다. 예를 들어 선 채로 엄마(일라스티 걸)의 팔다리가 늘어나 먼 곳에 있는 물체를 잡거나 마스크의 혀가 바닥에 계단처럼 펼쳐지는 장면에서 사용한다.

한편‘모핑(morphing)’은 *모피즘(morphism)이라는 수학용어에서 유래했다. 이는 어떤 사물의 모습을 아예 다른 모습으로 변화시키는 것을 말한다. 귀여운 막내(잭잭)가 갑자기 무시무시한 악마로 바뀌는 장면은 바로 모핑 기법을 이용한 것이다.

이 두 기법은 모두 원래 이미지와 변형시킬 이미지 사이의 대응점을 찾아 분석한다. 변형한 뒤에도 원래 모습의 점과 선이 끊어지지 않도록 만드는 것이 바로 수학적 원리와 아이디어를 이용한 것이다.

*모피즘(morphism)이란 두 수학적인 구조 사이의 관계를 뜻하는 용어다. 우리가 잘 알고 있는 집합 사이의 대응 관계를 나타내는‘함수’는 모피즘의 일부다.

위상기하학으로 살펴본 그녀의 초능력
 

애니메이션 속 엄마(일라스티 걸)는 전성기때 원더우먼에 버금가는 여성영웅이었다. 그런 그녀의 초능력이 뜻밖에도 수학의 원리와 닮았단다. 대체 어디가 닮았단 걸까? 앞에서 살펴본 영화 제작 기법이 이 문제의 커다란 힌트다. 그중 와핑 기법을 이용하면 변형한 뒤에도 원래 모습의 선과 면이 끊어지지 않고 이어진 상태로 변형된다. 그녀의 초능력에 적용된 수학의 비밀을 파헤쳐 보자.

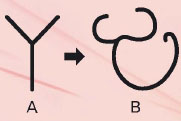
왼쪽 그림과 같이 Y자 모양으로 생긴 고무줄(A)을 아래위로 잡아당겨 B의 모습으로 만들어 보자. 이때 고무줄에 각각 어떤 기하학이 적용되느냐에 따라 두 고무줄은 같은 것 또는 다른 것일 수도 있다. 사실 우리가 학교에서 주로 공부하는‘유클리드 기하학’은 길이와 모양이 달라진 고무줄을 다른 것이라 여긴다. 유클리드 기하학은 길이와 모양이 같은 도형만을 같은 것으로 취급하기 때문이다.

하지만 길이와 모양이 달라진 도형도 같은 것이라 여기는 학문도 있다. 그것이 바로‘위상기하학’이다. 위상기하학에서는 모양이 아무리 변형돼도 그 도형의 본질적인 상태가 변하지 않는다면 모두 같은 도형이라 여긴다. 다시 말해 변형된 고무줄(B)에서 직선이 곡선이 되고, 길이가 달라졌지만 선을 구성하고 있는 점들의 배열순서가 변하지 않았다는 점에만 집중한다.

이처럼 길이와 모양이 달라졌지만 점들의 연속적인 배열순서가 같고 이어진 선과 면이 같다면 같은 도형이라 간주하는 이 너그러운 학문을 위상기하학이라 한다. 흔히‘고무판 위의 기하학’이라고도 부른다.

이를 이용하면 엄마(일라스티 걸)의 초능력을 훨씬 더 수학적으로 설명할 수 있다. 그녀의 주특기인 몸 구부리기, 팔다리 잡아 늘리기, 배 부분 부풀리기 등으로 변형된 몸도 모두 그녀의 몸에서 출발한것이니까. 그녀가 아무리 초능력을 발휘해 신체의 일부를 변형해도 그녀의 몸통에 팔다리가 연결돼 있는‘상태’는 변하지 않는다. 그녀가 변신하면서 팔다리의 위치까지 바꾸지 않기 때문에 신체의 각부위를 잇는 선들과 면들은 변하지 않는다. 따라서 그녀는 초능력 사용에 상관없이 원래의 모습으로 돌아올 수 있는 것이다.

고무줄처럼 변신하는 지하철 노선도
 

일상생활 속에서 그녀의 초능력과 같은 원리를 찾을 수 있을까? 물론이다. 위상기하학의 가장 큰 특징은 도형의 크기나 길이 등의‘양’에는 큰 관심을 기울이지 않는다는 점이다. 따라서 생활 속에서 종종 간소화하는 것들은 모두 이것의 좋은 예가 된다.

예를 들어 약속장소를 전혀 모르는 친구에게 장소를 설명해야 하는 상황이다. 여러분은 스마트 기기들을 이용해 설명할지도 모르겠지만, 가장 쉬운 방법은 약도를 그려 설명해주는 방법이다. 보통 친구에게 약도를 그려줄 때 모든 건물과 건물 사이, 도로와 도로 사이를 실제 거리로 그리지 않는다. 건물의 높이와 건물 사이의 거리를 정확히 알지 못해도 간단한 선과 네모 몇 개면 충분하다. 아마도 그가 발걸음 수를 세며 찾아오지 않을 테니까. 이는 그녀의 초능력을 설명한 원리와 많이 닮았다. 모습은 실제와 다르게 변형됐지만 같은 것이라 여기기 때문이다.

길거리에서 쉽게 볼 수 있는 버스 노선도나 지하철 노선도는 생활 속 깊숙이 들어와 있는 또 다른 예다. 두 노선도가 실제 지도와는 다르게 그려졌다는 사실은 누구나 안다. 대부분의 사람들은 서울 시내 어딘가에서 지하철을 타지 않은 채 지하철 노선도만 보고 서울역을 찾아갈 수 없을 테니까 말이다.만약 초능력이 있다면? 그것은 상상에 맡기겠다.

잘 알다시피 지하철 노선도는 동서남북의 방향과 그 거리를 무시한 채 그려졌다. 지하철을 이용해 출발지에서 목적지까지 이동할 경우 정확한 방향과 거리를 몰라도 무사히 도착할 수 있다. 그래서 지하철 노선도는 실제 지도와 다르게 간단히 그려져도 상관없다!

실제로 서울역과 시청역은 매우 가까이에 위치해 있고, 지하철 노선도에서도 한 정거장 차이다. 이를지하철 노선도로 만들기 위해 단순화 과정을 거쳤다고 해서 노선도에 그려진‘역’의 순서, 즉 점들의 연속적인 배열순서가 바뀌지 않는다. 이는 위상기하학의 눈으로 보면 같은 것이라 할 수 있다.

이럴 수가, 우리 몸속은 겉과 속의 구분이 없다고?!

위상기하학으로 세상을 바라보면 재미난 일들이 많다. 지금까지 살펴본 이야기보다 좀 더 복잡하고 공간적인 이야기를 들려주려고 한다.

위상기하학으로 우리 몸속을 들여다보면 겉과 속을 구분하기 힘들다. 아니 구분이 없다. 과연 진실일까? 진실을 파헤치기 전에, 두께가 있는 원기둥을 살펴보자.

두께가 있는 원기둥은 오른쪽 그림처럼 생긴 고무관을 상상하면 된다. 그 다음 도형 안쪽에 손가락을집어넣어 뒤집으면 겉과 속을 뒤바뀌꿀 수 있다. 이는 우리 몸속의 소화기관과도 비슷한 상황이다. 이제 입과 항문 사이를 연결하고 있는 소화기관에 집중해보자.

소화기관은 주머니 모양인 위를 제외하고는 모두 원형관이다. 입에서 출발해 항문을 향해‘손가락 여행’을 시작해 볼까? 흠…, 그림이니 걱정하지 말고 따라오시라.

음식물이 흘러가는 경로를 따라서 소화기관의 관을 거쳐 항문까지 이르면 손가락은‘몸속’이 아닌 ‘피부(겉)’로 나와 있다. 분명 입속으로 출발한 여행인데, 엉덩이(겉)에 도착했다. 또 엉덩이를 출발해 피부를 따라 입까지 올라와 뱃속으로 들어가니, 소화기관을 다시 만나게 된다. 여기는 다시 몸속이다!

이처럼 소화기관은 겉에서 볼 때 분명‘몸의 내부’이지만 위상기하학적으로 관찰해 보면‘몸의 외부’인 셈이다. 즉 정말 우리 몸속 소화기관은 겉과 속의 구분이 없다!

이처럼 위상기하학은 사물을 좀 더 유연하게 바라볼 수 있게 한다. 사실 요즘은 모든 것이 빠르게 변화하는 시대다. 자칫 잘못하면 새로운 변화만 쫓기도 바쁜 세상이지만 실제로는 겉모습만 봐서 알 수없는 것들이 많다.

다시 말해 눈앞에 보이는 것만을 중요하게 여기다 보면, 그 안에 숨겨진 본질적인 것을 놓칠 수도 있다는 얘기다. 이래서 세상 속에는 겉과 속을 자연스럽게 넘나드는 유연한 학문인‘위상기하학’이 더욱 필요한 것이 아닐까.