d라이브러리

새 연구소 소장인 튤리오 박사는 제가 꼭 만나야 할 친구가 있다며 절 새장에 가뒀어요. 누군가 제게‘비행’을 배우러 오나 봐요. 아니, 비행을 가르쳐야 하는데, 왜 가두는 겁니까? 친구는 또 무슨 소용이에요, 당장 드넓은 하늘을 날 수 없는데! 제 관심은 오직 비행, 비행뿐입니다.

사람들도 ‘하늘을 나는 것’ 에 대한 환상이 있잖아요. 오랜 연구 끝에 우리의 모습을 본떠 비행기를 만든 거고요. 이처럼 자유로운 비행은 새들의 특권이니, 늘 자랑스럽게 여기고, 늘 갈망하는 건 당연하다고 생각합니다. 하지만 새라고 해서 모두 같은 방법으로 하늘을 나는 건 아니에요. 자신의 신체특징을 살려 스스로 가장 유리한 방법으로 하늘을 날거든요.

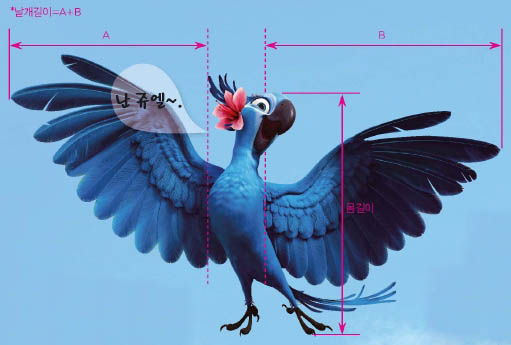
특히 새들은 날개길이 : 몸길이와 같이 자신에게 주어진 ‘비’ 를 기준으로 주로 쓰는 비행방법이 달라요. 전 보시다시피 날개길이가 몸길이보다 긴 편이어서 활공 비행에 유리한 편이죠. 활공 비행이란날갯짓이나 동력(예: 비행기가 엔진을 통해 받는 힘)없이 날개를 편 상태로 날아가는 것을 말합니다.보통 갈매기나 독수리처럼 날개길이가 몸길이에 비해 긴 새들이 활공 비행을 즐깁니다.

활공 비행을 얼마나 잘할 수 있느냐는 수학적으로 표현할 수 있는데, 이것을 ‘활공비’ 라고 해요. 활공비의 값이 클수록 동력 없이 더 멀리 날아갈 수 있고, 바람을 이용하면 잠깐이지만 하늘에 정지할 수도 있거든요. 엄청 매력적이죠. ♥_♥.
 

활공비는 수평으로 날아간 거리 : 하강한 높이, 비의 값은 수평으로 날아간 거리÷하강한 높이로 계산해요. 활공비는 간단한 수로 나타내고 a : b 꼴로 표현합니다. 예를 들어 활공비가 10 : 1이면 이 새는 100m 아래로 하강할 때마다 수평으로 1km(=1000m)만큼 날아갈 수 있는 있다는 뜻이죠.

서로 다른 활공비를 가진 새 또는 비행기는 비의 값을 구해 그들의 비행능력을 비교해요. 예를 들어 그림으로 살펴볼게요.
 

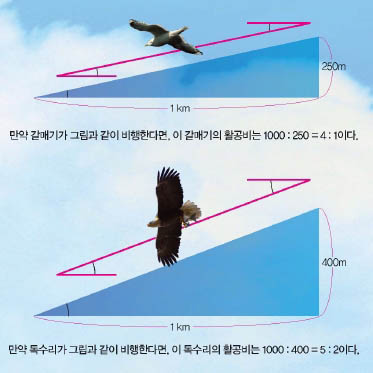
만약 갈매기와 독수리의 활공 능력이 위 그림과 같다면, 갈매기의 활공비의 값은 4로, 독수리의 활공비의 값 2.5보다 크죠. 이는 같은 높이에서 활공을 시작했을 때 날갯짓 없이 갈매기가 독수리보다 1.6배 더 멀리 날아갈 수 있다는 뜻입니다.

실컷 활공 비행에 대해 이야기하다 보니, 절 찾아온다는 친구 소개가 늦었네요. 미국에 사는 파란 앵무새 ‘블루’ 라던데…, 호호. 어찌나 소문이 빠른지, 벌써 미국까지 제 실력이 소문이 났네요. 녀석이 오기 전에 ‘비’ 와 관련한 내용을 마저 정리해야겠어요.

몸길이에 대한 날개길이의 비 외에도 활공 비행을 얼마나 잘하느냐는 날개의 가로·세로 길이와도 매우 밀접한 관련이 있어요. 활공 비행은 날개의 면적이 같더라도 가로 길이가 길고, 세로 길이가 짧을수록 유리하거든요.

날개의 가로·세로 비는 날개의 가로길이 : 날개의 세로길이를 말해요. 날개의 세로길이에 대한 가로길이의 비인 거죠. 비의 값은 다음과 같이 두 가지 방법으로 구할 수 있어요.
 

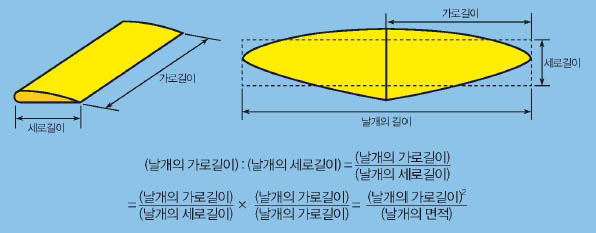
새들의 날개는 면적을 계산하기 어려우므로, 간단히 그린 비행기 날개 그림으로 자세히 설명할게요.
 

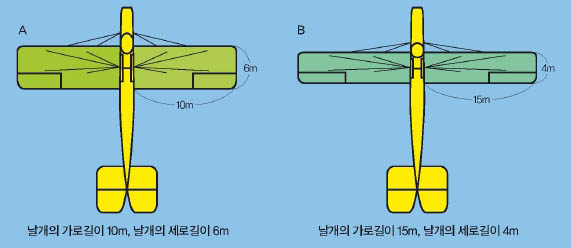
두 비행기 날개의 면적이 모두 60m2이라고 가정하고 각각의 가로·세로 비를 구해봅시다. A 비행기의 가로·세로 비는 10 : 6 = 5 : 3이며 비의 값은 약 1.67이고, B 비행기의 가로·세로 비는 15 : 4이며 비의 값은 3.75네요. 따라서 가로·세로 비의 값은 A 비행기보다 B 비행기가 더 크죠.

그림으로 살펴보면 확실히 B 비행기의 날개가 가로로 길고 세로로 좁잖아요. 새도 마찬가지예요. 날개의 가로길이가 길고, 세로길이가 짧을수록 가로·세로 비의 값과 활공비의 값이 커서 활공 비행에 유리한 거랍니다.

새들의 비행에는 날개 비율이 아주 중요해요. 물론 커다랗고 긴 날개를 가질수록 무조건 비행을 잘할것 같지만, 꼭 그런 건 아니에요. 본능적으로 각자 날개길이와 비에 가장 적합한 비행 방법을 깨닫는거죠.

저는 갈매기나 독수리보다 날개의 가로길이가 짧고 세로길이는 긴 편이어서 활공비의 값과 가로·세로 비의 값이 작아요. 제가 비록 그들보다 활공 비행으로 멀리 날지 못하지만, 파란 깃털은 누구보다 매력적이지 않나요? 헤헤.

tip 리오
애니메이션 ‘리오’ 는 브라질의 대표 항구도시 ‘리오데자네이로’ 를 배경으로 하고 있다. 제작진은 리오데자네이로의 약칭인 ‘리오’ 를 본떠 애니메이션의 제목으로 정했다. 리오는 1763년~1960년까지 브라질의 수도였고, 자연미와 인공미가 조화를 이룬 덕분에 세계에서 아름다운 항구도시로 손꼽힌다.매년 3~4월경 부활절 즈음에 이를 기념하는 대대적인 축제가 열린다.

새 날갯짓의 자취, 사이클로이드 곡선

‘사이클로이드’ 란 그리스어로 ‘바퀴’ 를 뜻한다. 사이클로이드 곡선이란 용어는 바퀴가 굴러간 자취에서 유래됐다. 사이클로이드 곡선의 성질은 프랑스의 수학자 파스칼이 처음 밝혔다.

사이클로이드 곡선은 두 지점 사이를 가장 빠르게 움직일 수 있는 곡선이다. 심지어 직선보다 빠르다. 사이클로이드 곡선의 시작지점 기울기가 직선의 시작지점 기울기보다 가파르기 때문이다.

주로 활공 비행을 하며 먹이를 사냥하는 독수리는 먹이를 최단시간에 낚아채기 위해, 목표물을 향해 직선으로 비행하지않고 사이클로이드 곡선에 가깝게 곡선 비행을 하며 먹이를 포획한다.

하늘을 나는 새의 날갯짓의 자취를 그래프로 나타내면 다음 그림과 같은 사이클로이드 곡선과 매우 흡사하다.
 

또한 새의 날개 끝은 몸통을 기준으로 할 때 사이클로이드 형태의 타원 모양으로 자취를 남기며 *양력을 이용해 앞으로 나아간다.

수학자들은 이 아름다운 성질을 트로이전쟁의 원인이 된 그리스 신화에 등장하는 최고의 미녀 헬레네의 아름다움에 빗대어 ‘기하학의 헬레네’ 라 부른다.

*양력

날개의 윗면과 아랫면의 기압 차이로 인해 발생하는 힘이다. 이는 새 또는 비행기를 공중에 날 수 있도록 하는 힘이다.

활공 비행에 유리한 비행기 날개

활공 비행에 유리한 비행기를 만들려면 무조건 가로·세로 비의 값이 큰 날개를 만들어야 할까? 아니다. 가로·세로 비의 값이 커질수록 활공 비행은 유리할 수 있지만, 그 값이 클수록 비행기 날개를 단단하게 만들기는 어렵다. 따라서 보통 항공기는 가로·세로 비의 값이 8.5 미만이다. 또한 고속으로 비행하는 항공기일수록 날개의 단단한 정도는 매우 중요하므로, 실제로 가로·세로 비의 값이 작은 날개를 사용한다. 고속항공기의 경우 가로·세로 비의 값이 3.0~3.5로 작은 것도 있다.

스픽스마코앵무

마코앵무(금강앵무)는 남북아메리카대륙의 고유 앵무새로 부리와 몸집이 크고 화려하다. 그래서 사람들이 마구 잡아 그 수가 감소해 멸종위기에 처해 있다. 브라질에는 독특한 마코앵무가 많이 서식하는데, 특히 전 세계에서 딱 4종(큰푸른마코앵무, 유리마코앵무, 쇠푸른마코앵무, 스픽스마코앵무)뿐인 온몸이 파란 마코앵무가 산다. 애니메이션 ‘리오’ 에 등장하는 ‘블루’ 와 ‘쥬엘’ 은 이 중 스픽스마코앵무에 해당한다. 안타깝게도 현재 스픽스마코앵무는 야생에서는 멸종한 것으로 추정된다.


▼관련기사를 계속 보시려면?

INTRO 떴다 떴다 비행기~♬ 수학으로 날아라!
PART 1 비를 알면 비행이 보인다
PART 2 각을 알면 비행이 보인다 
PART 3 힘을 알면 비행이 보인다
PART 4 수학으로 날아오른 블루의 첫 비행