d라이브러리

가을 운동회 후 친구와 함께 피자를 배달시켰다.

그런데 이게 t웬걸? 피자가 이상하게 잘려 왔다. 조각마다 중심각은 45가 맞는데 피자를 나눈 그 중심이 한쪽으로 치우쳐 있다. 친구와 공평하게 나눠 먹을 방법이 있을까? ‘피자 정리’를 통해 문제를 해결해 보자.

공평하게 피자를 나누는 방법, 피자 정리

‘피자 정리’는 1967년 캐나다 온타리오 주에 사는 업튼 씨가 미국수학협회에서 발행하는 <;수학 잡지>;의 독자 코너에 문제 하나를 출제하면서 시작된다.

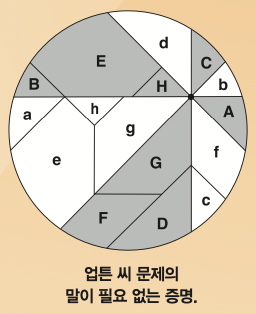
머지않아 미국 수학자 마이클 골드버그가 문제를 해결했고, 그 풀이 과정이 다음 호 <;수학 잡지>;에 실린다. 27년의 세월이 흐른 1994년 래리 카터와 스탠리 웨건이라는 두 명의 수학자가 그림 한 장으로 이 문제의 답을 설명해 보인다. 이러한 방법을 ‘말이 필요 없는 증명’이라고 하는데, 두 수학자는 아래쪽 그림처럼 영어 알파벳의 대문자와 소문자로 대응하는 영역이 서로 합동이 되게 도형을 나눠 면적이 같음을 보였다.

이후에도 업튼 씨의 문제는 출제된지 50년이 넘는 시간 동안 여러 수학자에 의해 재구성됐다. 먼저 8조각이 아닐 때는 어떨까? 2012년 미국 수학자 그렉 프레드릭슨은 12조각, 16조각 등 4배수의 조각에 대해서도 면적이 같은 두 영역으로 나눌 수 있음을 증명했다.

이 문제를 그림으로 나타내면 마치 피자를 조각낸 것 같아서, n개의 조각으로 일반화한 문제를 피자 정리라 한다.

만약 두 사람이 피자를 나눠 먹는 상황이 아닐 땐 어떨까? 이에 대한 대답은 1999년 허쉬혼 일가의 증명에서 찾을 수 있다.

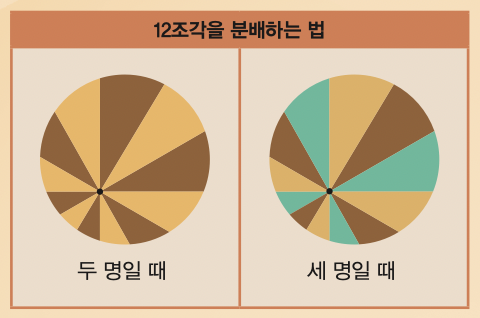
n명이 피자를 나누는 경우, 피자 위의 한 점에서 같은 각도로 나뉘도록 2n개의 직선으로 자르면 4n개의 조각이 생기고, 한 명씩 번갈아가며 같은 크기의 조각을 하나씩 가져가면 모두 같은 양을 갖게 된다는 것이다. 즉, 이 증명에 따라 12조각으로 나눠진 피자는 두 명이든, 세 명이든 공평하게 나눌 수 있다. 이 정도면 피자 정리를 세상에서 가장 맛있는 정리라고 말해도 되지 않을까?