d라이브러리

자, 이제 반 친구들에 대해 어느 정도 알게 됐어. 그러면 뭘 하면 좋을까? 맞았어. 앞으로 일 년 동안 생활할 준비를 해야겠지. 번호도 정하고 앉는 자리도 확실히 정하는 등 할 일이 많단다. 이래서 새학기는 눈코 뜰 새 없이 바쁘게 지나가는 법이야.

먼저 선생님께서 뭐라고 하시는지 들어보자. 아~, 먼저 키를 가지고 번호를 정하자고 하시네.


줄을 서시오~!

얼른 일어나서 줄을 서도록 하자. 작은 친구는 앞으로 큰 친구는 뒤로….

하아~, 그런데 그렇게 여러 사람이 맞는 자리를 찾느라 우왕좌왕하니까 순서대로 줄을 서기가 힘들지? 선생님도 힘드신 모양이야. 어떡하면 선생님을 도와 쉽게 순서대로 설 수 있을까?

아무렇게나 서 있는 친구들을 키 순서대로 정렬해 보자. 멋대로 섞여 있는 수를 순서대로 정렬하는 방법에는 여러 가지가 있어. 예를 들어, 키가 각각 150cm, 165cm, 157cm, 163cm, 153cm인 친구 5명이 있을 때 키 순서대로 정렬해 보자.


1. 옆하고만 비교해

한 수와 바로 옆의 수를 비교해 순서대로 바꿔주는 방법이다. 서로 붙어 있는 두 수를 차례로 비교해 순서가 거꾸로면 바꿔준다.

이와 같은 과정을 최대 4번 반복.
 

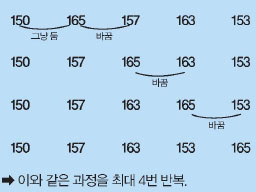
첫 번째는 서로 붙어 있는 두 수를 순서대로 비교하는 방법이야. 이런 과정을 반복하다보면 결국 모든 수가 순서대로 정렬돼. 정렬할 수가 n개일 때 최대 (n-1)번 반복하면 완벽히 정렬할 수 있지.

(n-1)번인 이유는 가장 큰 수가 맨 앞에 있다고 했을 때 그 수가 맨 뒤로 가려면 (n-1)번만 바꿔 주면 된다는 사실을 생각하면 이해하기 쉬워.


2. 골라서 비교해

가장 앞에 있는 수부터 차례로 나머지 수와 비교해 가면서 순서가 거꾸로면 바꿔주는 방법이다.

정렬 끝!
 

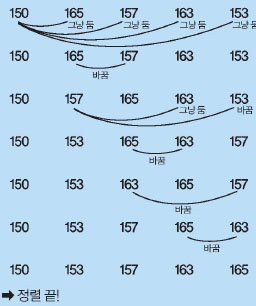
두 번째는 앞에서부터 순서대로 한 수와 뒤에 있는 나머지 수를 모두 비교하는 방법이야. 이 방법은 첫 번째 방법보다 2~3배 빠르단다.

정렬해야 하는 수가 많아질수록 눈으로 보고 적당히 정렬하기 힘들어. 그래서 이와같은 방법을 고안해 쓰는 거야. 실제로 컴퓨터 프로그램을 이용해 자료를 정렬할 때는 이런 방법을 이용해. 물론 좀 더 복잡한 원리를 쓰면 이보다 더 빠르게 정렬할 수도 있어. 어떤 방법을 쓰면 더 효율적으로 정렬할 수 있을지 궁리해 보자고~.


그래프가 대칭이야!

휴우~, 이제야 드디어 순서대로 줄을 섰구나. 이렇게 나란히 서 있는 모습을 보니 반 친구들의 키를 그래프로 나타낼 수 있겠다는 생각이 들어. 번호가 뒤로 갈수록 키가 커지니 다음과 같은 그래프가 되겠지.
 

그런데 가로축을 번호가 아닌 키로 바꾸면 그래프의 모양이 이렇게 바뀌어.
 

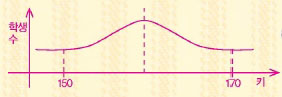
두 번째 그래프와 같은 모양, 즉 도수를 나타내는 곡선이 평균을 중앙으로 좌우대칭을 이루는 모양을 수학에서는 정상분포 또는 정규분포라고 해. 반 친구들의 키를 나타낸 그래프가 정규분포를 이룬다는 말은 키가 평균에 가까운 친구들의 수가 가장 많고 크거나 작은 쪽으로 갈수록 비슷하게 줄어든다는 뜻이야. 키뿐만 아니라 반 친구들의 성적 또한 그래프를 그리면 정규분포를 이루지.


나누고 뽑고!

여러분도 번호를 받았지? 그러면 자리로 돌아가 앉도록 하자. 잠깐! 자리에 앉기 전에 할 일이 있어. 아까는 여러분이 아무렇게나 앉은 자리였지? 하지만 이제는 진짜로 자리를 정해서 앉아야 해. 선생님 말씀에 따라 모둠을 나눠서 앉기로 하자.
 

나는 어느 모둠, 회장은 누구?

남자와 여자가 골고루 섞이게 모둠을 나누자고 하시네. 그런데 또다시 아무렇게나 모아 놓으면 뒤죽박죽이 될 거야. 처음부터 깔끔하게 남자와 여자가 각각 몇 명씩 들어가는지 정하고 모둠을 나눠야 할 텐데, 과연 어떻게 하면 될까?

각 모둠마다 남자와 여자가 똑같은 수로 들어가도록 모둠을 나눌 때는 최대공약수를 개념을 이용하면 돼. 어떤 정수를 나눴을 때 나누어떨어지는 수를 그 정수의 약수라고 하지. 두 정수가 있을 때 두 정수 공통의 약수를 공약수라고 하고, 공약수 중에서 가장 큰 수가 바로 최대공약수야.

최대공약수 찾기
남학생 16명과 여학생 12명인 반에서 모둠을 나눈다면 16과 12의 최대공약수를 구해 보자.
16의 약수 - 1, 2, 4, 8, 16
12의 약수 - 1, 2, 3, 4, 6, 12

따라서 최대공약수는 4야. 이 때 최대공약수만큼 모둠을 만들면 남자와 여자를 모둠마다 똑같이 넣을 수 있어. 이 경우 4모둠으로 나누면 각각의 모둠에는 남학생 4명과 여학생 3명이 들어가.

골고루 모둠을 나눠 앉았으니 같은 모둠의 친구들과 인사를 하렴. 당분간 교실에서 가장 가까이 지낼 친구들이니까 말이야.

자, 잠깐~! 그렇다고 해서 그렇게 오래 떠들며 인사만 하고 있으면 안 돼. 아직은 수업 시간이잖아. 게다가 아직 새학기 준비를 마치려면 중요한 일 한 가지를 더 해야 한다고. 바로 회장과 부회장을 뽑는 거야.

놀라지 마. 바로 여러분이 회장과 부회장 후보로 뽑혔어. 기왕 이렇게 된 거 열심히 해 보라고. 그런데 뭐라고? 아까부터 은근히 눈에 들어오던 아이, 그 아이와 함께 회장이 되고 싶다고?

임원까지 뽑았으니 이제 새학기 준비가 끝났어. 오늘은 일단 집으로 돌아가도록 하자고. 워워~, 또다시 잠깐. 그냥 가면 어떡해? 청소는 하고 가야지~, 흐흐. 자, 그러면 각 모둠에서 청소당번 한 명씩을 알아서 뽑도록. 어떻게 뽑냐고? 음, 사다리 타기를 이용하면 어떨까?

사다리로 보는 일대일 대응

사다리를 그리고 세로 기둥 하나에 한 명씩 대응시키는 거야. 사다리를 따라 내려다가보면…, 당첨! 청소당번은 바로 너!

사다리 타기는 수학에서 중요한 개념인 일대일대응에 대해 알려 줘.
 

가장 간단한 사다리는 이렇게 1과 B가 짝지워지고, 2와 A가 짝지워지지.
 

그런데 가로줄을 하나 더 그으면 1과 A가, 2와 B가 짝지워져. 대응은 바뀌었지만 줄을 더 그어도 숫자 하나에 알파벳 하나가 대응되는 건 똑같아. 숫자 2개가 똑같은 알파벳에 대응되는 일은 일어나지 않는 거지. 그건 아무리 줄을 많이 그어 복잡한 사다리라고 해도 일대일대응의 원리에 따라 하나에 하나씩만 대응된다는 뜻이지.


일대일대응의 원리란?

일대일대응은 두 집합의 원소가 하나도 빠지거나 남지않고 둘씩 짝지워지는 대응을 말한다.
수학의 기초인 수와 사물을 짝짓는 행위에도 바로 이 일대일대응의 원리가 담겨있다.



▼관련기사를 계속 보시려면?

수학으로 푸는 두근두근 새학기 
PART 1 두근두근 새학기 시작! 그리운 옛 친구, 반가운 새 친구
PART 2 정신없다, 새학기 준비! 나란히~ 나란히~ 키 번호 정하기 
PART 3 완전 기대 새학기 생활! 수학은 공평해 
새학기 특별 보너스 새학기 증후군? 문제 없어!