
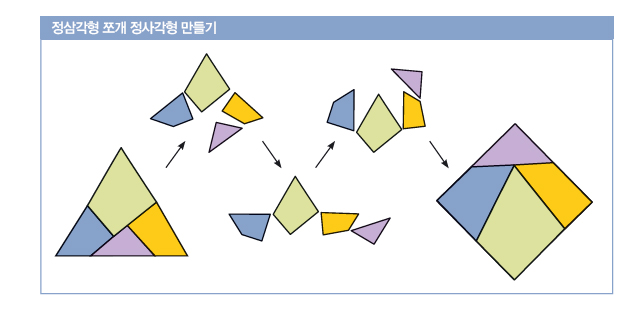
정삼각형을 잘라서 정사각형을 만들 수 있을까요? 아래 그림과 같이 정삼각형을 4개 조각으로 잘라서 조립하면 가능합니다.
정삼각형을 다각형으로 확장하면 어떨까요? 평면에 넓이는 같지만 모양은 다른 두 다각형이 있을때 하나를 잘라서 다른 다각형으로 만들 수 있냐는 겁니다. 이 질문의 답은 놀랍게도 ‘예’입니다. 1807년 영국 수학자 윌리엄 월레스가 이 사실을 증명했지요. 월레스가 이미 정답을 알았다는 사실을 몰랐던 파울 게르빈과 퍼르커시 보여이도 각각 1833년과 1835년에 서로 다른 방법으로 문제를 풀었습니다. 그래서 현재 이 문제를 ‘월레스-보여이-게르빈 정리’라고 부릅니다.
1900년 프랑스 파리에서 열린 세계수학자대회에서 독일 수학자 다비트 힐베르트는 이 정리를 확장한 문제를 20세기에 꼭 풀어야 할 23문제 중 하나로 발표했습니다.
힐베르트 3번 문제
부피가 같은 두 다면체가 있을 때, 다면체 하나를
유한 조각으로 잘라 다른 다면체로 항상 조립할 수 있을까?
힐베르트는 문제가 어렵다고 생각해서 23문제 중 하나로 골랐겠지만, 당시 힐베르트의 제자였던 막스 덴이 곧바로 문제를 풀었습니다. 덴은 다면체를 자르고 조립하는 과정에서 변하지 않는 도형의 성질에 ‘덴 불변량’이라는 이름을 붙이고 이 값을 살펴봤습니다. 그리고 이 값이 다른 다면체가 있다는 것을 보여 문제의 답이 ‘아니오’라는걸 밝혔지요.
이때까지는 도형을 잘라서 붙일 때 각 조각의 경계면에 있는 점은 크게 신경을 쓰지 않았습니다. 예를 들어 사각형을 반으로 잘라 두 조각으로 만들면 경계면에 있던 점은 왼쪽 조각에도 있고 오른쪽 조각에도 있다고 볼 수 있지요. 이런 두 조각을 붙이면 경계면에 있던 두 점은 한 점이 돼버립니다. 만약 이점까지 고려해 점이 한쪽 조각으로 간다고 정해도 앞서 살펴봤던 결과와 같을까요?

문제를 좀 더 편하게 풀기 위해 집합 용어를 사용합시다. 다각형을 점의 집합으로 생각하면, 다각형의 분할은 점을 유한개의 집합으로 나누는게 됩니다. 각 점을 평행이동하고 회전이동하면서 다각형을 조립하게 되지요. 이처럼 점을 여러 집합으로 나누고 대칭이동해서 넓이가 같은 다른 모양의 다각형을 만들 수 있을까요?
끊임없이 만들어지는 공, 바나흐-타르스키 역설
1924년 폴란드 수학자 알프레트 타르스키는 점까지 까다롭게 분할해도 월레스-보여이-게르빈 정리가 성립한다고 밝혔습니다. 타르스키는 같은 해 폴란드 수학자 스테판 바나흐와 함께 구에 관해 다음과 같은 재밌는 문제를 풀었습니다.
바나흐-타르스키 역설
3차원에서 공 1개를 집합 5개로 잘 분할한 다음,
잘 조립하면 처음 공과 같은 크기의 공 2개로
만들 수 있다.
공 1개로 크기가 같은 공 2개를 만들 수 있다니 이상하지요? 그런데 이게 수학적으로 사실이라니 놀랍기만 합니다. 사실 이 역설대로 공(구)을 분할하려고 하면 각 집합은 부피가 정의되지 않는 이상한 형태의 조각이 됩니다. 즉 우리가 상상하는 그런 조각이 아니라 매우 이상한 점의 집합이 돼서 조각을 새로 조립하면 원래 부피의 2개가 됩니다.

쉽사리 상상이 가질 않지요? 도형의 조각이 이 처럼 이상한 점의 집합이어도 된다면 우리의 상식을 벗어난 신기한 현상이 일어납니다. 필자도 대학생 시절 바나흐-타르스키 역설을 처음 배울 때 혼란스러웠던 기억이 아직도 생생합니다.
원을 쪼개 정사각형으로 만들기
그런데 2차원에서는 바나흐-타르스키 역설과 같은 일이 벌어지지 않습니다. 1923년 바나흐가 원을 아무리 많은 조각으로 쪼갰다가 합쳐도 조각의 수가 유한개라면 넓이가 변하지 않는다는 것을 보였지요. 그렇다면 원을 쪼개 넓이가 같은 정사각형을 만들 수 있을까요?
타르스키 문제
평면에서 속이 꽉 찬 원을 유한개로 분할한 다음
조립해 원래의 원과 같은 넓이의 속이 꽉 찬
정사각형을 만들 수 있을까?
원은 테두리가 구부러져 있으니 아무리 잘 잘라도 정사각형을 만들 수 없을 것 같습니다. 이 상식이 맞기라도 한 듯 1963년 세 명의 미국 수학자 레스터 두빈스, 모리스 허쉬, 윌리엄 카루쉬는 원을 가위로 잘라서는 어떻게 자르고 조립해도 정사각형을 만들 수 없다는 것을 증명했습니다.
하지만 1990년 헝가리의 수학자 미클로시 러츠코비치는 상식을 깬 답을 찾았습니다. 타르스키 문제에 대한 답이 ‘예’라는 것을 증명한 겁니다. 러츠코비치는 속이 꽉 찬 원을 1040개의 점의 집합으로 잘 나누면 각 집합을 잘 평행이동한 뒤 모아서 넓이가 같은 정사각형을 만들 수 있다고 밝혔지요. 다만 이때 각 조각은 바나흐-타르스키 역설에서처럼 넓이가 정의되지 않는 이상한 형태입니다. 넓이를 알 수 있는 조각으로 원을 나눠 정사각형을 만들 수는 없을까요?
2017년 3월, 이 질문에 대한 답이 수학계 최고 학술지 중 하나인 수학연보에 실렸습니다. 영국 랭카스터대학교의 루카스츠 그라보브슈키 박사, 언드라시 마테 영국 워릭대학교 교수, 올레크 피크후르코 워릭대 교수는 원을 유한개 집합으로 잘 분할하면 넓이도 정의되고, 각 집합을 평행이동만 해서 정사각형을 만들 수 있다는 걸 증명했습니다. 하지만 이 증명에서 생기는 집합의 수는 러츠코비치의 1040보다 좀 더 많습니다.
정말로 1040개 이상의 집합으로 나눠야 할까요? 좀 더 좋은 증명을 통해 더 작은 수로 나눌 수는 없을까요? 집합이 얼마나 필요한지 참 궁금합니다.
※ 엄상일 교수는 KAIST 수학과를 졸업하고, 미국 프린스턴대학교에서 박사 학위를 받았습니다. 현재는 KAIST에서 강의와 연구를 하고 있습니다. 그래프이론과 이산수학, 조합적 최적화가 주요 연구 분야입니다. 2012년에는 젊은과학자상(대통령상)을 수상했고, 2017년에는 한국차세대과학기술한림원 회원으로 선정됐습니다.












