파라메트릭 곡선으로 만드는 몸통
배우에게 외모는 첫인상을 결정하는 요소입니다. 캐릭터의 경우 배역에 어울리는 외모를 갖춰야 합니다. 영화 ‘도리를 찾아서’의 도리와 니모는 컴퓨터 그래픽으로 만들어졌지만 진짜 물고기처럼 부드럽고 매끈한 몸통을 갖췄어요. 동글동글한 외모가 귀여운 매력을 더욱 끌어올리지요?

지금도 애니메이터는 애니메이션 영화를 만들기에 앞서 캐릭터의 생김새와 표정을 손으로 예쁘게 그립니다. ‘컨셉을 잡는다’고 하지요. 하지만 컴퓨터는 이렇게 그린 캐릭터를 인식하지 못합니다. 컴퓨터가 3차원 캐릭터를 인식할 수 있도록 표현하는 방법이 필요합니다.
1972년, 미국의 컴퓨터 개발자인 애드윈 캣멀은 단편 영화에서 여러 가지 다각형으로 뒤덮은 3차원 손을 선보였습니다. 삼각형이나 사각형으로 표면을 감싼 캐릭터는 부피감이 느껴지면서도 컴퓨터가 점과 선으로 캐릭터를 인식할 수 있습니다. 이렇게 캐릭터를 나타내는 것을 ‘폴리곤 메쉬’라고
하며, 캐릭터의 몸통을 만드는 ‘모델링’ 단계에서 널리 쓰였습니다.

다각형이 맞닿아 있는 부분은 자세히 보면 마치 표면이 꺾인 것 처럼 보입니다. 도리를 자세히 들여다봤을 때 피부가 모난 듯 꺾여있다면 무척 부자연스러울 겁니다. 다각형으로 이뤄진 캐릭터의 몸통에서 점 몇 개를 잡고, 이 점으로 굉장히 부드러운 곡선을 그릴 수는 없을까요?
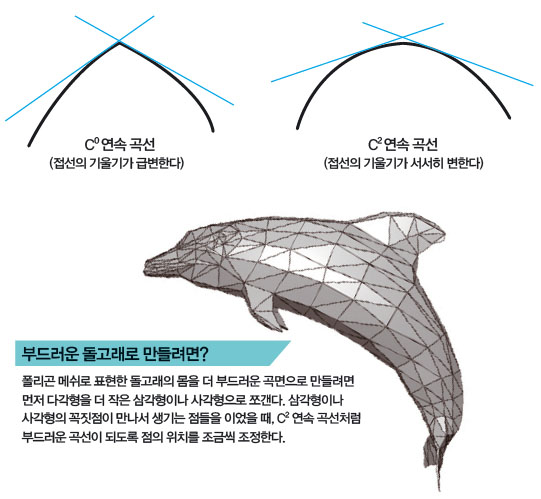
몇 개의 점을 이어서 곡선을 그려보겠습니다. 그 중에는 끊어지지는 않았지만 뾰족한 부분이 있는 경우가 있습니다. 이 곡선 위의 점에서 곡선에 접하는 접선을 그려보세요. 아마 뾰족한 부분 근처에서 접선의 기울기가 갑자기 크게 변할 겁니다. 원래 곡선의 식을 한 번 미분★한 결과인 기울기가 급변하는 것을 ‘기울기가 연속적이지 않다’고 표현해요.
‘한 번도 미분하지 않은 상태에서만 연속인 곡선’을 ‘C0 연속 곡선’이라고 합니다. 이와 달리 한 번 미분한 결과인 기울기까지 연속인 곡선을 ‘C1 연속 곡선’, 두 번 미분한 결과까지 연속인 곡선을 ‘C2 연속 곡선’이라고 합니다. 여러 번 미분한 결과까지 연속인 곡선일수록 부드러워 보이지요.
이런 곡선의 성질을 고려해 3D 캐릭터를 부드럽게 표현하는 용도로 고안한 곡선을 ‘파라메트릭 곡선’이라고 합니다. 캐릭터를 모델링할 때 많이 쓰는 ‘넙스 곡선’도 파라메트릭 곡선의 한 종류랍니다. 폴리곤 메쉬를 응용한 기술과 파라메트릭 곡선, 두 가지 방법이 함께 쓰여 캐릭터를 진짜처럼 만듭니다.
피부의 완성은 적분!
영화 ‘빅 히어로’의 로봇 ‘베이맥스’는 비닐 풍선에 바람을 채운 듯 푹신푹신해 보입니다. 영화 ‘주먹왕 랄프’ 속 나이든 신사의 벗겨진 이마는 반질반질, 딸기코는 발그레하지요. 비닐에 바람을 채우고, 코에도 물감을 칠해야만 할 것 같은 이들의 분장은 놀랍게도 ‘적분’으로 충분히 완성할 수 있답니다.
투명하고 쨍한 피부, 부드러운 피부, 속이 불투명하고 딱딱한 피부는 모두 ‘빛’을 조절해 만듭니다. 조명에서 나온 빛줄기의 경로를 계산해서 원하는 피부를 만들 수 있지요. 빛줄기의 경로란, 조명에서 나온 빛이 캐릭터의 표면에서 반사돼 카메라의 렌즈로 들어가기까지의 길을 뜻합니다. 빛의 경로와 빛의 세기
를 계산해 캐릭터에 질감과 색깔을 입히는 과정을 ‘렌더링’이라고 합니다.
조명에서 나오는 무한히 많은 빛줄기의 경로를 모두 추적하기는 거의 불가능 합니다. 그 중에는 캐릭터의 표면에서 반사된 뒤에 카메라 렌즈 바깥으로 뻗어나가는 빛도 있습니다. 렌즈 안으로 들어오지 않으면 사람이 볼 수 없기 때문에 경로를 추적할 필요가 없는 빛이지요.


거꾸로, 빛이 카메라에서 나와 캐릭터의 표면에 부딪힌 다음 조명으로 들어간다고 상상해 보세요. 카메라로 들어오는 꼭 필요한 빛을 훨씬 적은 계산으로 추적할 수 있습니다. 이렇게 골라낸 빛줄기가 결국 조명에서 나와 캐릭터의 표면에 부딪힌 뒤 카메라의 렌즈로 들어가는 빛인 셈이거든요. 꼭 필요한 빛만 고려하니까 계산을 줄일 수 있지요.
캐릭터의 표면 위 한 점에 부딪히는 빛줄기가 많을수록 그 부분은 환하고 부드럽게 보이고, 빛줄기가 적을수록 어둡게 보인답니다.

적분으로 빛줄기를 모아라!
마지막으로, 눈에 보이지 않는 수많은 빛줄기를 모두 더하는 건 ‘적분’의 몫입니다. 우선 만들려는 캐
릭터 표면 위의 한 점에 접하는 반구를 그립니다. 그 다음 반구 속으로 들어오는 빛줄기를 나타내는 벡터 함수를 적분합니다. 적분은 곧 ‘모두 더한다’는 뜻입니다.
이때 캐릭터의 피부가 원래 빛을 잘 반사시키는지 아닌지도 고려해야 합니다. 그래서 얼굴의 경우, 피
부의 반사율을 뜻하는 함수를 빛의 세기와 방향을 나타내는 벡터 함수에 곱하지요. 반사율 함수의 값
이 클수록 피부가 밝겠지요?
만약 피부가 유리처럼 투명한 캐릭터라면 조명에서 날아온 빛의 일부가 몸통의 표면 안쪽으로 들어가 몸통 안에서도 여러 번 반사될 겁니다. 이렇게 몸통 안에서 반사되는 빛의 세기도 계산해야 할 때는 캐릭터의 표면 위 한 점을 중심으로 하는 ‘구’를 그립니다. 즉, 적분 영역이 반구면 불투명한 피부, 구면 투명한 피부가 됩니다.
행렬이 조종하는 표정
분장을 마친 캐릭터 배우는 대사를 읊으며 연기 연습을 합니다. 실제 동물을 촬영한 것과 차이가 거의 없는 디지털 캐릭터의 경우 표정 연기도 아주 섬세하지요. 영화 ‘정글북’에 나오는 여러 동물 캐릭터가 그렇습니다. 컴퓨터 그래픽으로 만든 캐릭터가 연기 수업이라도 받는 것인지, 수학동아가 파헤쳐봤습니다.
컴퓨터로 만드는 디지털 캐릭터의 경우, 짓고 싶은 표정을 컴퓨터 그래픽으로 만들어야 합니다. 이때 쓰는 대표적인 방법이 ‘표정 섞기’입니다. 여러 가지 표정을 섞어 새로운 표정을 만드는 방법이지요. 한 번도 지은 적 없는 새 표정을 만들려면 우선 기준이 되는 ‘무표정’한 얼굴이 필요합니다. 무표정한 얼굴을 변형해 여러 가지 표정을 만드는 겁니다.
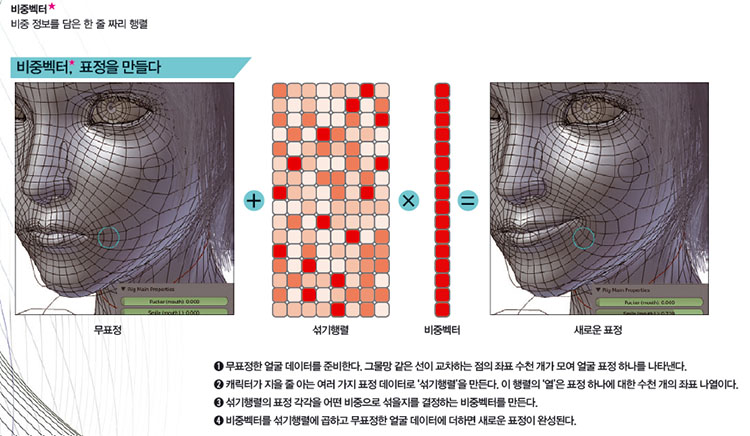
사람이 지을 수 있는 표정은 수천 가지가 넘습니다. 표정을 지을 때 눈썹, 광대, 입꼬리 등이 움직이고, 얼굴 위에 찍은 점의 위치가 달라지지요. 이때 얼굴 위 점의 좌표를 (x, y, z)로 나타내면 표정을 숫자의 나열인 행렬로 바꿀 수 있습니다. 무표정을 뜻하는 행렬에 수많은 표정 정보를 담은 행렬을 더하면 전에 없던 새로운 표정 행렬을 만들 수 있습니다.

자연스러운 표정 돕는 확률 모형
비중벡터를 이루는 값을 어떻게 결정하는지에 따라 여러 가지 새로운 표정이 나옵니다. 그런데 어떤 비
중벡터로 좌표 데이터를 만들어야 원하는 표정이 나올지는 알 수 없습니다.
원하는 표정이 나올 때까지 일일이 비중벡터의 숫자를 조절한다면 아주 힘들고 시간이 오래 걸릴겁니다. 그래서 실제 배우의 얼굴 곳곳에 마커를 붙이고 근육의 움직임을 자동으로 기록하는 ‘모션 캡처’ 기술을 이용합니다. 마커를 쓰면 100개 남짓한 좌표를 얻을 수 있는데, 표정을 정확히 나타내려면 좌표가 수천~수만 개나 필요하기 때문에 정보가 부족합니다.
이때 선택하는 방법이 바로 ‘확률’. 사람이 지을 수 있는 표정 데이터로 만든 확률 분포와 모션 캡처로 만든 표정 데이터를 비교합니다. 이 확률 분포의 한가운데에는 실제로 사람이 지을법한 여러 가지 표정 좌표의 평균값이 있습니다. 그래서 모션 캡처로 만든 표정 데이터가 확률 분포의 중앙에 가까울수록 진짜 사람이나 동물처럼 자연스러운 표정이 될 확률이 높습니다. 반대로 중앙에서 멀어질수록 어딘가 부자연스러운 표정이 될 확률이 높지요. 만약 확률 분포의 도움 없이 행렬을 구한다면 웃을 때 입꼬리가 코에 붙어버리는 것처럼 아주 이상한 표정이 나올지도 모릅니다. 행렬은 계산만 할 뿐 ‘자연스러움’은 전혀 모르거든요.

방정식이 만드는 동작
컴퓨터 그래픽으로 만든 캐릭터 배우는 가상의 3차원 공간에서 자유롭게 연기합니다. 대본에 있는 대로 허리 굽혀 인사도 하고 때로는 춤도 춥니다. 컵에서 찰랑대는 우유, 창문을 타고 흐르는 빗물처럼 영화에 필요한 소품과 날씨도 생생하지요. 모두 방정식 덕분이랍니다.
겉보기에 아무리 살아있는 것 같아도 캐릭터가 제 스스로 몸을 움직일 수는 없습니다. 팔을 접었다 펴는 간단한 행동도 할 수 없지요. 그래서 캐릭터가 움직이는 것처럼 ‘보이는’ 방법이 필요합니다.
물론 움직이기만 한다고 다 자연스럽게 보이지는 않습니다. 팔을 접을 때 팔뚝의 근육도 움직이고, 팔꿈치 주변의 피부도 약간 눌려야 훨씬 진짜 같지요. 그래서 캐릭터의 뼈대와 뼈대를 잇는 관절마다 가상의 좌표축을 심습니다. 그러면 관절이 움직일 때 근처에 있는 피부의 점도 함께 움직이도록 계산할 수 있지요.
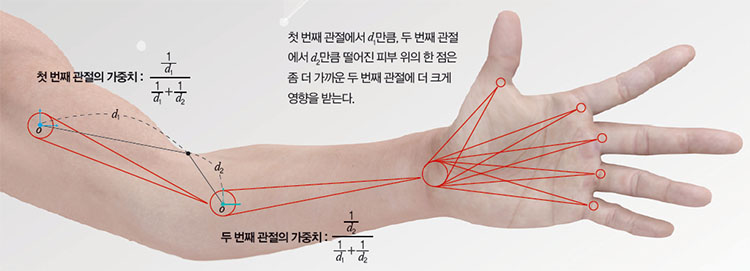
피부에 있는 한 점의 좌표는 근처에 있는 관절이 얼마나 움직이는지에 따라 움직입니다. 그리고 가까이 있는 관절일수록 더 크게 영향을 받지요. 그래서 가까운 관절이 움직이는 정도에 더 큰 가중치(중요한 정도를 나타내는 값)를 곱합니다. 고려해야 하는 관절의 개수가 많을수록 피부의 변형을 계산하는 방정식이 더 복잡해지지요.

미분방정식 따라 졸졸졸
캐릭터가 우유를 컵에 따르는 장면도 마찬가지입니다. 우유팩에 담긴 우유가 컵으로 떨어지면 컵 안쪽에 우유가 부딪힙니다. 우유는 점점 차오르면서 출렁이지요. 우유 방울은 시시각각 다르게 움직입니다. 영화 ‘슈렉’에서 이 장면을 수학적으로 구현하는 작업에 참여한 이화여대 수학과 민조홍 교수는 뉴턴의 운동방정식 ‘F(힘)=m(질량)×a(가속도)’가 중요한 원리라고 설명했습니다. 이 운동방정식 안에는 가속도 항이 있는데, 가속도는 속도를 미분한 결과입니다. 그래서 일종의 미분방정식★이기도 하지요.

사실 이 방정식을 풀기는 너무나 복잡해서 이 방정식을 좀 더 간단하게 만든 방정식의 해를 구합니다. 이 해를 통해 우유가 컵 안으로 자연스럽게 흐르는 장면을 만들 수 있지요. 수학자들은 여기서 그치지 않고 원래 미분방정식의 해와 아주 가까운 해의 성질을 밝히는 데 도전하고 있습니다.
[미분방정식★어떤 함수의 도함수(미분한 결과)를 포함하는 방정식.]

배우에게 외모는 첫인상을 결정하는 요소입니다. 캐릭터의 경우 배역에 어울리는 외모를 갖춰야 합니다. 영화 ‘도리를 찾아서’의 도리와 니모는 컴퓨터 그래픽으로 만들어졌지만 진짜 물고기처럼 부드럽고 매끈한 몸통을 갖췄어요. 동글동글한 외모가 귀여운 매력을 더욱 끌어올리지요?

지금도 애니메이터는 애니메이션 영화를 만들기에 앞서 캐릭터의 생김새와 표정을 손으로 예쁘게 그립니다. ‘컨셉을 잡는다’고 하지요. 하지만 컴퓨터는 이렇게 그린 캐릭터를 인식하지 못합니다. 컴퓨터가 3차원 캐릭터를 인식할 수 있도록 표현하는 방법이 필요합니다.
1972년, 미국의 컴퓨터 개발자인 애드윈 캣멀은 단편 영화에서 여러 가지 다각형으로 뒤덮은 3차원 손을 선보였습니다. 삼각형이나 사각형으로 표면을 감싼 캐릭터는 부피감이 느껴지면서도 컴퓨터가 점과 선으로 캐릭터를 인식할 수 있습니다. 이렇게 캐릭터를 나타내는 것을 ‘폴리곤 메쉬’라고
하며, 캐릭터의 몸통을 만드는 ‘모델링’ 단계에서 널리 쓰였습니다.

다각형이 맞닿아 있는 부분은 자세히 보면 마치 표면이 꺾인 것 처럼 보입니다. 도리를 자세히 들여다봤을 때 피부가 모난 듯 꺾여있다면 무척 부자연스러울 겁니다. 다각형으로 이뤄진 캐릭터의 몸통에서 점 몇 개를 잡고, 이 점으로 굉장히 부드러운 곡선을 그릴 수는 없을까요?
몇 개의 점을 이어서 곡선을 그려보겠습니다. 그 중에는 끊어지지는 않았지만 뾰족한 부분이 있는 경우가 있습니다. 이 곡선 위의 점에서 곡선에 접하는 접선을 그려보세요. 아마 뾰족한 부분 근처에서 접선의 기울기가 갑자기 크게 변할 겁니다. 원래 곡선의 식을 한 번 미분★한 결과인 기울기가 급변하는 것을 ‘기울기가 연속적이지 않다’고 표현해요.
‘한 번도 미분하지 않은 상태에서만 연속인 곡선’을 ‘C0 연속 곡선’이라고 합니다. 이와 달리 한 번 미분한 결과인 기울기까지 연속인 곡선을 ‘C1 연속 곡선’, 두 번 미분한 결과까지 연속인 곡선을 ‘C2 연속 곡선’이라고 합니다. 여러 번 미분한 결과까지 연속인 곡선일수록 부드러워 보이지요.
이런 곡선의 성질을 고려해 3D 캐릭터를 부드럽게 표현하는 용도로 고안한 곡선을 ‘파라메트릭 곡선’이라고 합니다. 캐릭터를 모델링할 때 많이 쓰는 ‘넙스 곡선’도 파라메트릭 곡선의 한 종류랍니다. 폴리곤 메쉬를 응용한 기술과 파라메트릭 곡선, 두 가지 방법이 함께 쓰여 캐릭터를 진짜처럼 만듭니다.

피부의 완성은 적분!
영화 ‘빅 히어로’의 로봇 ‘베이맥스’는 비닐 풍선에 바람을 채운 듯 푹신푹신해 보입니다. 영화 ‘주먹왕 랄프’ 속 나이든 신사의 벗겨진 이마는 반질반질, 딸기코는 발그레하지요. 비닐에 바람을 채우고, 코에도 물감을 칠해야만 할 것 같은 이들의 분장은 놀랍게도 ‘적분’으로 충분히 완성할 수 있답니다.
투명하고 쨍한 피부, 부드러운 피부, 속이 불투명하고 딱딱한 피부는 모두 ‘빛’을 조절해 만듭니다. 조명에서 나온 빛줄기의 경로를 계산해서 원하는 피부를 만들 수 있지요. 빛줄기의 경로란, 조명에서 나온 빛이 캐릭터의 표면에서 반사돼 카메라의 렌즈로 들어가기까지의 길을 뜻합니다. 빛의 경로와 빛의 세기
를 계산해 캐릭터에 질감과 색깔을 입히는 과정을 ‘렌더링’이라고 합니다.
조명에서 나오는 무한히 많은 빛줄기의 경로를 모두 추적하기는 거의 불가능 합니다. 그 중에는 캐릭터의 표면에서 반사된 뒤에 카메라 렌즈 바깥으로 뻗어나가는 빛도 있습니다. 렌즈 안으로 들어오지 않으면 사람이 볼 수 없기 때문에 경로를 추적할 필요가 없는 빛이지요.


거꾸로, 빛이 카메라에서 나와 캐릭터의 표면에 부딪힌 다음 조명으로 들어간다고 상상해 보세요. 카메라로 들어오는 꼭 필요한 빛을 훨씬 적은 계산으로 추적할 수 있습니다. 이렇게 골라낸 빛줄기가 결국 조명에서 나와 캐릭터의 표면에 부딪힌 뒤 카메라의 렌즈로 들어가는 빛인 셈이거든요. 꼭 필요한 빛만 고려하니까 계산을 줄일 수 있지요.
캐릭터의 표면 위 한 점에 부딪히는 빛줄기가 많을수록 그 부분은 환하고 부드럽게 보이고, 빛줄기가 적을수록 어둡게 보인답니다.

적분으로 빛줄기를 모아라!
마지막으로, 눈에 보이지 않는 수많은 빛줄기를 모두 더하는 건 ‘적분’의 몫입니다. 우선 만들려는 캐
릭터 표면 위의 한 점에 접하는 반구를 그립니다. 그 다음 반구 속으로 들어오는 빛줄기를 나타내는 벡터 함수를 적분합니다. 적분은 곧 ‘모두 더한다’는 뜻입니다.
이때 캐릭터의 피부가 원래 빛을 잘 반사시키는지 아닌지도 고려해야 합니다. 그래서 얼굴의 경우, 피
부의 반사율을 뜻하는 함수를 빛의 세기와 방향을 나타내는 벡터 함수에 곱하지요. 반사율 함수의 값
이 클수록 피부가 밝겠지요?
만약 피부가 유리처럼 투명한 캐릭터라면 조명에서 날아온 빛의 일부가 몸통의 표면 안쪽으로 들어가 몸통 안에서도 여러 번 반사될 겁니다. 이렇게 몸통 안에서 반사되는 빛의 세기도 계산해야 할 때는 캐릭터의 표면 위 한 점을 중심으로 하는 ‘구’를 그립니다. 즉, 적분 영역이 반구면 불투명한 피부, 구면 투명한 피부가 됩니다.

행렬이 조종하는 표정
분장을 마친 캐릭터 배우는 대사를 읊으며 연기 연습을 합니다. 실제 동물을 촬영한 것과 차이가 거의 없는 디지털 캐릭터의 경우 표정 연기도 아주 섬세하지요. 영화 ‘정글북’에 나오는 여러 동물 캐릭터가 그렇습니다. 컴퓨터 그래픽으로 만든 캐릭터가 연기 수업이라도 받는 것인지, 수학동아가 파헤쳐봤습니다.
컴퓨터로 만드는 디지털 캐릭터의 경우, 짓고 싶은 표정을 컴퓨터 그래픽으로 만들어야 합니다. 이때 쓰는 대표적인 방법이 ‘표정 섞기’입니다. 여러 가지 표정을 섞어 새로운 표정을 만드는 방법이지요. 한 번도 지은 적 없는 새 표정을 만들려면 우선 기준이 되는 ‘무표정’한 얼굴이 필요합니다. 무표정한 얼굴을 변형해 여러 가지 표정을 만드는 겁니다.
사람이 지을 수 있는 표정은 수천 가지가 넘습니다. 표정을 지을 때 눈썹, 광대, 입꼬리 등이 움직이고, 얼굴 위에 찍은 점의 위치가 달라지지요. 이때 얼굴 위 점의 좌표를 (x, y, z)로 나타내면 표정을 숫자의 나열인 행렬로 바꿀 수 있습니다. 무표정을 뜻하는 행렬에 수많은 표정 정보를 담은 행렬을 더하면 전에 없던 새로운 표정 행렬을 만들 수 있습니다.


자연스러운 표정 돕는 확률 모형
비중벡터를 이루는 값을 어떻게 결정하는지에 따라 여러 가지 새로운 표정이 나옵니다. 그런데 어떤 비
중벡터로 좌표 데이터를 만들어야 원하는 표정이 나올지는 알 수 없습니다.
원하는 표정이 나올 때까지 일일이 비중벡터의 숫자를 조절한다면 아주 힘들고 시간이 오래 걸릴겁니다. 그래서 실제 배우의 얼굴 곳곳에 마커를 붙이고 근육의 움직임을 자동으로 기록하는 ‘모션 캡처’ 기술을 이용합니다. 마커를 쓰면 100개 남짓한 좌표를 얻을 수 있는데, 표정을 정확히 나타내려면 좌표가 수천~수만 개나 필요하기 때문에 정보가 부족합니다.
이때 선택하는 방법이 바로 ‘확률’. 사람이 지을 수 있는 표정 데이터로 만든 확률 분포와 모션 캡처로 만든 표정 데이터를 비교합니다. 이 확률 분포의 한가운데에는 실제로 사람이 지을법한 여러 가지 표정 좌표의 평균값이 있습니다. 그래서 모션 캡처로 만든 표정 데이터가 확률 분포의 중앙에 가까울수록 진짜 사람이나 동물처럼 자연스러운 표정이 될 확률이 높습니다. 반대로 중앙에서 멀어질수록 어딘가 부자연스러운 표정이 될 확률이 높지요. 만약 확률 분포의 도움 없이 행렬을 구한다면 웃을 때 입꼬리가 코에 붙어버리는 것처럼 아주 이상한 표정이 나올지도 모릅니다. 행렬은 계산만 할 뿐 ‘자연스러움’은 전혀 모르거든요.

방정식이 만드는 동작
컴퓨터 그래픽으로 만든 캐릭터 배우는 가상의 3차원 공간에서 자유롭게 연기합니다. 대본에 있는 대로 허리 굽혀 인사도 하고 때로는 춤도 춥니다. 컵에서 찰랑대는 우유, 창문을 타고 흐르는 빗물처럼 영화에 필요한 소품과 날씨도 생생하지요. 모두 방정식 덕분이랍니다.
겉보기에 아무리 살아있는 것 같아도 캐릭터가 제 스스로 몸을 움직일 수는 없습니다. 팔을 접었다 펴는 간단한 행동도 할 수 없지요. 그래서 캐릭터가 움직이는 것처럼 ‘보이는’ 방법이 필요합니다.
물론 움직이기만 한다고 다 자연스럽게 보이지는 않습니다. 팔을 접을 때 팔뚝의 근육도 움직이고, 팔꿈치 주변의 피부도 약간 눌려야 훨씬 진짜 같지요. 그래서 캐릭터의 뼈대와 뼈대를 잇는 관절마다 가상의 좌표축을 심습니다. 그러면 관절이 움직일 때 근처에 있는 피부의 점도 함께 움직이도록 계산할 수 있지요.
피부에 있는 한 점의 좌표는 근처에 있는 관절이 얼마나 움직이는지에 따라 움직입니다. 그리고 가까이 있는 관절일수록 더 크게 영향을 받지요. 그래서 가까운 관절이 움직이는 정도에 더 큰 가중치(중요한 정도를 나타내는 값)를 곱합니다. 고려해야 하는 관절의 개수가 많을수록 피부의 변형을 계산하는 방정식이 더 복잡해지지요.


미분방정식 따라 졸졸졸
캐릭터가 우유를 컵에 따르는 장면도 마찬가지입니다. 우유팩에 담긴 우유가 컵으로 떨어지면 컵 안쪽에 우유가 부딪힙니다. 우유는 점점 차오르면서 출렁이지요. 우유 방울은 시시각각 다르게 움직입니다. 영화 ‘슈렉’에서 이 장면을 수학적으로 구현하는 작업에 참여한 이화여대 수학과 민조홍 교수는 뉴턴의 운동방정식 ‘F(힘)=m(질량)×a(가속도)’가 중요한 원리라고 설명했습니다. 이 운동방정식 안에는 가속도 항이 있는데, 가속도는 속도를 미분한 결과입니다. 그래서 일종의 미분방정식★이기도 하지요.

사실 이 방정식을 풀기는 너무나 복잡해서 이 방정식을 좀 더 간단하게 만든 방정식의 해를 구합니다. 이 해를 통해 우유가 컵 안으로 자연스럽게 흐르는 장면을 만들 수 있지요. 수학자들은 여기서 그치지 않고 원래 미분방정식의 해와 아주 가까운 해의 성질을 밝히는 데 도전하고 있습니다.
[미분방정식★어떤 함수의 도함수(미분한 결과)를 포함하는 방정식.]












