기원전 5~6세기경 찬란한 철학적 사고를 개발했던 그리스인들은 물질에 대해서도 철학적 이론을 제시했다. 불과 물, 흙, 공기가 서로 조합해서 물질을 만든다는 주장이다. 오늘날의 관점에서는 이해하기 어려운 말이다. 물질을 구성하는 것은 뭔가 물질보다 더 단순한 것이어야 할 텐데, 물과 불, 흙, 공기는 이미 그 자체가 물질이라 다른 물질에 비해 더 단순하지 않다. 오직 데모크리토스만이 물질을 이해하는 올바른 패러다임을 제시했다. “물질의 근원이 뭔지 알고 싶으면 쪼개라! 쪼개고 또 쪼개면 결국 그 물질의 근원이 나올 것이다!” 하지만 물질을 영원히 계속 쪼갤 수 있다면 결국 아무 것도 남지 않을 테니 언젠가는 더 이상 쪼갤 수 없는 단위에 다다를 것이다. 이때 우리는 ‘더 이상 쪼갤 수 없다’는 의미의 멋진 단어, ‘원자(Atom)’와 마주하게 된다.
그리스 철인들의 꿈을 이룬 ‘양자역학’
데모크리토스의 개념적 원자로부터 양자역학적, 물리적 원자에 도달하기까지 대략 24세기의 세월이 들었으니, 한 세대를 30년으로 치면 어림 80세대쯤 걸렸다. 1926년 슈뢰딩거 방정식의 등장으로, 원자를 이해하는 것은 수학 방정식을 푸는 문제로 바뀌었다. 양자역학으로 원자라는 문제를 풀게 된 물리학자들은 곧 원자들의 집단, 그러니까 고체라는 한 차원 복잡한 문제를 양자역학적으로 해결하고자 도전했다.
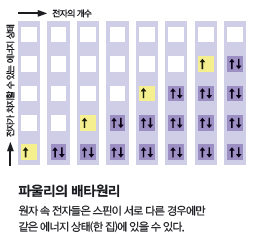
원자를 단독주택이라고 한다면 고체는 거대한 아파트다. 원자핵 주위를 돌고 있는 전자는 집에 거주하는 사람에 해당한다. 고체는 매우 개방적인 체계를 갖춘 곳이어서, 누구나 어떤 집에든 거주할 수 있는 자격이 있다. 다만 매우 독특한 조건이 하나 있는데, 집 한 채에 동시에 남자 두 명이, 혹은 여자 두 명이 거주하는 것은 ‘법’으로 금지돼 있다(남성 여성에 해당하는 전자의 속성을 스핀이라고 부르며, 이 자연법칙을 ‘파울리의 배타원리’라고 한다). 반면 남자와 여자가 각각 한 명씩 한 집에 거주하는 것은 괜찮다. 또 다른 특징이 있다. 이 아파트엔 출입문이 없다! 다른 집으로 옮겨 가고 싶으면 벽을 뚫고 가야 한다. 인간은 해낼 수 없는 이 마술 같은 일이 전자에겐 쉬운 일이다. 전자는 입자인 동시에 파동이다. 마치 옆집의 TV 소리가 벽을 통해 전달되듯, 전자는 벽을 통해 옆집으로 이동할 수 있다. 눈에 보이지 않는 터널이라도 있는 것 같다고 해서 이런 현상을 ‘터널 효과’라고 한다.
어떤 아파트 건물의 모든 가구에 남자 한명과 여자 한 명이 함께 살고 있다고 하자. 남남 금지법과 여여 금지법 때문에 이런 상황에서는 남자도, 여자도 옆집으로 이동할 수 없다. 옆집에 이미 동성이 거주하고 있으므로 모든 사람이 자기 집에서 꼼짝도 못하는 상황이다. 이 상황에 해당하는 고체가 바로 절연체, 전기가 통하지 못하는 물질이다.
반면 어떤 아파트 건물에는 가구 당 남자, 혹은 여자 한 명씩만 살고 있다. 이런 상황이라면 비교적 자유롭게 아파트 전체를 돌아다닐 수 있다. 바로 금속 상태에서 벌어지는 현상이다. 자, 이로써 양자역학을 이용해 고체와 부도체의 차이를 완벽히 이해할 수 있게 됐다.
전자의 기묘한 군무가 바꿔놓은 물질관
물질이란 말 대신 양자물질이라는 용어가 본격적으로 회자된 것은 21세기에 들어선 이후다. 금과 은, 구리, 철은 여전히 물질이라고 부른다. 양자물질의 범주에는 실험실에서 합성된 인조물질과, 위상학적 특성이 강하게 드러나는 위상물질, 혹은 양자컴퓨터 소자로 쓰일 만한 물질군이 포함된다. 양자물질은 현대 물리학을 주도하는 운동의 한 축이자, (역사적으로 계속 벌어져 왔던) 입자물리학과 응집물질물리학의 간극을 좁히고 통합 시키는 새로운 마당이 되고 있다.
그리스 철인들의 꿈을 이룬 ‘양자역학’
데모크리토스의 개념적 원자로부터 양자역학적, 물리적 원자에 도달하기까지 대략 24세기의 세월이 들었으니, 한 세대를 30년으로 치면 어림 80세대쯤 걸렸다. 1926년 슈뢰딩거 방정식의 등장으로, 원자를 이해하는 것은 수학 방정식을 푸는 문제로 바뀌었다. 양자역학으로 원자라는 문제를 풀게 된 물리학자들은 곧 원자들의 집단, 그러니까 고체라는 한 차원 복잡한 문제를 양자역학적으로 해결하고자 도전했다.
원자를 단독주택이라고 한다면 고체는 거대한 아파트다. 원자핵 주위를 돌고 있는 전자는 집에 거주하는 사람에 해당한다. 고체는 매우 개방적인 체계를 갖춘 곳이어서, 누구나 어떤 집에든 거주할 수 있는 자격이 있다. 다만 매우 독특한 조건이 하나 있는데, 집 한 채에 동시에 남자 두 명이, 혹은 여자 두 명이 거주하는 것은 ‘법’으로 금지돼 있다(남성 여성에 해당하는 전자의 속성을 스핀이라고 부르며, 이 자연법칙을 ‘파울리의 배타원리’라고 한다). 반면 남자와 여자가 각각 한 명씩 한 집에 거주하는 것은 괜찮다. 또 다른 특징이 있다. 이 아파트엔 출입문이 없다! 다른 집으로 옮겨 가고 싶으면 벽을 뚫고 가야 한다. 인간은 해낼 수 없는 이 마술 같은 일이 전자에겐 쉬운 일이다. 전자는 입자인 동시에 파동이다. 마치 옆집의 TV 소리가 벽을 통해 전달되듯, 전자는 벽을 통해 옆집으로 이동할 수 있다. 눈에 보이지 않는 터널이라도 있는 것 같다고 해서 이런 현상을 ‘터널 효과’라고 한다.
어떤 아파트 건물의 모든 가구에 남자 한명과 여자 한 명이 함께 살고 있다고 하자. 남남 금지법과 여여 금지법 때문에 이런 상황에서는 남자도, 여자도 옆집으로 이동할 수 없다. 옆집에 이미 동성이 거주하고 있으므로 모든 사람이 자기 집에서 꼼짝도 못하는 상황이다. 이 상황에 해당하는 고체가 바로 절연체, 전기가 통하지 못하는 물질이다.
반면 어떤 아파트 건물에는 가구 당 남자, 혹은 여자 한 명씩만 살고 있다. 이런 상황이라면 비교적 자유롭게 아파트 전체를 돌아다닐 수 있다. 바로 금속 상태에서 벌어지는 현상이다. 자, 이로써 양자역학을 이용해 고체와 부도체의 차이를 완벽히 이해할 수 있게 됐다.
전자의 기묘한 군무가 바꿔놓은 물질관
물질이란 말 대신 양자물질이라는 용어가 본격적으로 회자된 것은 21세기에 들어선 이후다. 금과 은, 구리, 철은 여전히 물질이라고 부른다. 양자물질의 범주에는 실험실에서 합성된 인조물질과, 위상학적 특성이 강하게 드러나는 위상물질, 혹은 양자컴퓨터 소자로 쓰일 만한 물질군이 포함된다. 양자물질은 현대 물리학을 주도하는 운동의 한 축이자, (역사적으로 계속 벌어져 왔던) 입자물리학과 응집물질물리학의 간극을 좁히고 통합 시키는 새로운 마당이 되고 있다.
1980년 독일 물리학자 클라우스 폰 클리칭이 발견한 양자 홀 효과는, 원자가 아닌 물질에서도 양자역학적인 현상이 일어난다는 사실을 보여준 충격적인 사건이었다. 양자홀 효과는 전류량을 전압으로 나눈 값인 홀 전도도가 정수 또는 분수인 경우로 나뉘는데, 괴짜 천재로 유명한 로버트 러플린은 분수 양자 홀 효과를 설명하는 기발한 이론을 1983년에 발표했다.

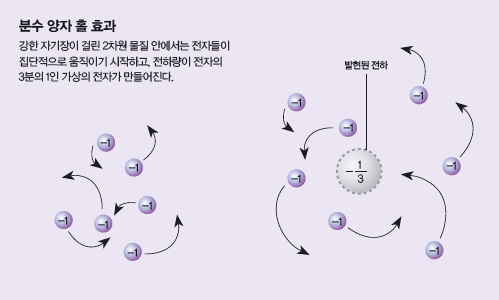
그 설명은 이렇다. 아주 얇아 두께를 논할 수 없는 2차원 물질을 만들어 그 안에 전자를 가둔다. 그리고 수직 방향으로 아주 강한 자기장(문구점에서 파는 자석보다 100배쯤 강한)을 걸어 준다. 그러면 전자는 개별적으로 행동하기를 멈추고 분수 양자 홀이라고 불리는 특이한 집단적 상태로 재조직된다. 운동장에 수천 명의 학생이 마구잡이로 뛰어 놀다가, 어떤 신호를 받는 순간 갑자기 가장 가까운 곳에 있는 친구와 팔을 걸고 빙글빙글 돌기 시작하는 모습을 상상해 보라. 또 다른 친구가 가까이 오면 이번엔 그 친구와 팔을 걸고 빙글빙글 돈다. 운동장에 있는 수천 명의 학생들이 일제히, 동일한 규칙에 맞춰 서로서로 빙글빙글 돌기 시작한다. 전자가 이렇게 집단 무용을 하는 것이 분수 양자홀 상태다.
모든 사람이 똑같은 속도로 회전을 하는 대신 일부 춤추는 쌍이 남들보다 빠른 속도로 회전하면 어떻게 될까? 원심력 때문에 그 두 사람 사이의 간격은 좀 더 벌어질 것이고, 따라서 가운데에 빈 공간이 생길 것이다. 그 공간의 크기는 사람 한 명이 더 들어오기에는 조금 좁다. 정확히 말하면 사람의 3분의 1이 들어오면 딱 맞을 만한 공간이 생긴다. 분수 홀 전자계에서 정확히 이런 일이 생긴다. 전하량이 전자의 3분의 1밖에 안 되는 상태가 만들어진다(67쪽 그림 참조). 오직 전자로만 구성된 자연계에서 전자보다 작은 전하를 만들어낼 때 이것을 ‘발현된(emergent) 전하’라고 부른다. 러플린 덕분에 이제 분수 전하를 가진 쿼크 같은 기본 입자조차도 이런 발현성의 결과라고 볼 수 있게 됐다. 기본 입자가 꼭 기본적이지만은 않을 수도 있다는 뜻이다. 러플린의 발견은 이후에 이어진 흐름, 기본 입자를 응집물질의 발현된 현상으로 재해석하는 흐름의 시초가 됐다.
광자 따라하는 그래핀 속 전자들
운동장에 수천 명의 어린아이를 풀어 놓으면, 가장 자연스러운 상태는 난장판이다. 이런 아이들을 길들여 분수 양자 홀이라는 군무를 수행하게 하려면 어마어마한 압력이 필요하다. 어린아이들의 활력(물리학에서는 운동에너지라고 부른다)을 모두 제거해 버린 뒤, 춤추는 좀비처럼 만들어야 하기 때문이다. 클리칭의 실험에서는 강한 자기장이 압력을 주는 역할을 했다. 하지만 이런 강압적 방법(물리학에서는 강한 상호작용이라고 부른다) 대신 대칭성과 위상학이라는 좀 더 우아한 방법을 통해, 전자들에게 다른 입자를 흉내 내도록 연기를 시킬 수도 있다.
그래핀은 연필심의 재료인 흑연(석탄)을 잘 벗겨서 만든 한 장짜리 흑연이다. 연필심에 전기가 통하는 것처럼 그래핀에도 전기가 흐른다. 전자가 움직이기 때문이다. 물리학에서는 입자의 움직임을 운동량과 에너지의 관계식으로 표현한다. 보통 입자의 에너지는 운동량의 제곱과 비례하고 질량에 반비례한다. 그런데 그래핀의 전자는 에너지가 운동량에 정비례한다. 좀 이상한(?) 일이다. 질량이 없는 광자에서나 벌어지는 현상이기 때문이다.
상대성이론에 따르면, 질량이 없는 입자는 에너지가 운동량에 비례한다. 그래핀의 전자가 상대론적 입자를 흉내 내고 있다는 뜻이다. 전자는 유한한 질량을 갖고 있으니 결코 상대론적 입자가 될 수 없다. 질량 있는 비상대론적 전자들이 모여 질량 없는 상대론적 입자를 흉내 내고 있는 꼴이다. 왜 그래핀의 전자는 상대론적으로 움직일까. 답은 그래핀의 벌집 모양 격자 구조에 있다. 육각격자가 갖는 독특한 대칭성 때문에 에너지와 운동량이 서로 비례해야 한다는 점을 증명할 수 있다. 상대론적 양자역학을 완성한 위대한 이론물리학자 폴 디랙의 이름을 따서 그래핀을 2차원 디랙 물질이라고 부른다.
모든 사람이 똑같은 속도로 회전을 하는 대신 일부 춤추는 쌍이 남들보다 빠른 속도로 회전하면 어떻게 될까? 원심력 때문에 그 두 사람 사이의 간격은 좀 더 벌어질 것이고, 따라서 가운데에 빈 공간이 생길 것이다. 그 공간의 크기는 사람 한 명이 더 들어오기에는 조금 좁다. 정확히 말하면 사람의 3분의 1이 들어오면 딱 맞을 만한 공간이 생긴다. 분수 홀 전자계에서 정확히 이런 일이 생긴다. 전하량이 전자의 3분의 1밖에 안 되는 상태가 만들어진다(67쪽 그림 참조). 오직 전자로만 구성된 자연계에서 전자보다 작은 전하를 만들어낼 때 이것을 ‘발현된(emergent) 전하’라고 부른다. 러플린 덕분에 이제 분수 전하를 가진 쿼크 같은 기본 입자조차도 이런 발현성의 결과라고 볼 수 있게 됐다. 기본 입자가 꼭 기본적이지만은 않을 수도 있다는 뜻이다. 러플린의 발견은 이후에 이어진 흐름, 기본 입자를 응집물질의 발현된 현상으로 재해석하는 흐름의 시초가 됐다.
광자 따라하는 그래핀 속 전자들
운동장에 수천 명의 어린아이를 풀어 놓으면, 가장 자연스러운 상태는 난장판이다. 이런 아이들을 길들여 분수 양자 홀이라는 군무를 수행하게 하려면 어마어마한 압력이 필요하다. 어린아이들의 활력(물리학에서는 운동에너지라고 부른다)을 모두 제거해 버린 뒤, 춤추는 좀비처럼 만들어야 하기 때문이다. 클리칭의 실험에서는 강한 자기장이 압력을 주는 역할을 했다. 하지만 이런 강압적 방법(물리학에서는 강한 상호작용이라고 부른다) 대신 대칭성과 위상학이라는 좀 더 우아한 방법을 통해, 전자들에게 다른 입자를 흉내 내도록 연기를 시킬 수도 있다.
그래핀은 연필심의 재료인 흑연(석탄)을 잘 벗겨서 만든 한 장짜리 흑연이다. 연필심에 전기가 통하는 것처럼 그래핀에도 전기가 흐른다. 전자가 움직이기 때문이다. 물리학에서는 입자의 움직임을 운동량과 에너지의 관계식으로 표현한다. 보통 입자의 에너지는 운동량의 제곱과 비례하고 질량에 반비례한다. 그런데 그래핀의 전자는 에너지가 운동량에 정비례한다. 좀 이상한(?) 일이다. 질량이 없는 광자에서나 벌어지는 현상이기 때문이다.
상대성이론에 따르면, 질량이 없는 입자는 에너지가 운동량에 비례한다. 그래핀의 전자가 상대론적 입자를 흉내 내고 있다는 뜻이다. 전자는 유한한 질량을 갖고 있으니 결코 상대론적 입자가 될 수 없다. 질량 있는 비상대론적 전자들이 모여 질량 없는 상대론적 입자를 흉내 내고 있는 꼴이다. 왜 그래핀의 전자는 상대론적으로 움직일까. 답은 그래핀의 벌집 모양 격자 구조에 있다. 육각격자가 갖는 독특한 대칭성 때문에 에너지와 운동량이 서로 비례해야 한다는 점을 증명할 수 있다. 상대론적 양자역학을 완성한 위대한 이론물리학자 폴 디랙의 이름을 따서 그래핀을 2차원 디랙 물질이라고 부른다.
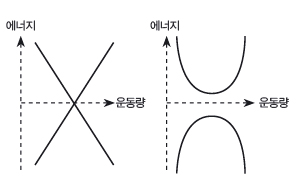
이 관계를 그래프로(x축이 운동량, y축이 에너지) 나타내면, 그래핀의 전자는 X자 모양의 직선형 그래프(위쪽 왼편)를, 보통의 물질에서는 위아래로 오목한 2차함수 포물선을 그린다. 그리고 물질 안에서 전자들은 실제로 이 에너지 상태에 자리잡고 있다. 절연체의 경우 포물선의 아래쪽에 해당하는 에너지 영역에 전자들이 분포해 있는 반면, 금속은 위쪽 포물선 에너지 영역에까지 전자들이 있어서 전류가 흐를 수 있다. 전자가 차지할 수 없는 공간(위 아래 포물선 사이)이 도체와 절연체를 나누는 분기점이라고 할 수 있다. 그래핀처럼 X자 모양의 그래프에는 이 분기점이 없어서 일종의 도체 상태라고 할 수 있다.
전자의 상대론 흉내 내기는 2차원 물질에서만 발견되는 현상이 아니다. 3차원에서 상대론적으로 움직이는 입자라면 그 에너지 역시 운동량에 비례할 것이다. 3차원 고체에서 이렇게 움직이는 전자를 찾을 수 있다. 3차원 디랙 물질인 위상절연체다.
3차원 상대론적 전자가 만드는 기묘한 물질, 위상절연체
디랙 방정식에 따르면, 상대론적 입자(디랙입자)는 움직이는 방향을 축으로 했을 때 시계 방향, 혹은 반시계 방향으로 뱅글뱅글 돌아야만 하는 제약이 있다. 입자의 스핀이라고 하는 것이 있어 이 스핀의 방향이 입자가 움직이는 방향과 나란하든지, 정반대로 나란하든지 둘 중 하나다. 그리고 빨간(시계방향 회전) 입자와 파란(반시계방향 회전) 입자는 늘 샴쌍둥이처럼 같이 있어야 한다(아래 그림_디랙 입자의 움직임과 에너지 띠 구조).
전자의 상대론 흉내 내기는 2차원 물질에서만 발견되는 현상이 아니다. 3차원에서 상대론적으로 움직이는 입자라면 그 에너지 역시 운동량에 비례할 것이다. 3차원 고체에서 이렇게 움직이는 전자를 찾을 수 있다. 3차원 디랙 물질인 위상절연체다.
3차원 상대론적 전자가 만드는 기묘한 물질, 위상절연체
디랙 방정식에 따르면, 상대론적 입자(디랙입자)는 움직이는 방향을 축으로 했을 때 시계 방향, 혹은 반시계 방향으로 뱅글뱅글 돌아야만 하는 제약이 있다. 입자의 스핀이라고 하는 것이 있어 이 스핀의 방향이 입자가 움직이는 방향과 나란하든지, 정반대로 나란하든지 둘 중 하나다. 그리고 빨간(시계방향 회전) 입자와 파란(반시계방향 회전) 입자는 늘 샴쌍둥이처럼 같이 있어야 한다(아래 그림_디랙 입자의 움직임과 에너지 띠 구조).
이제 1cm3의 고체 덩어리가 있다고 치자. 물리학자가 아니라면 전자가 어디 있느냐는 물음에 1cm3의 공간 속 어디엔가 있다고 대답할 것이다. 하지만 응집물질물리학자는 이보다 세련된 양자역학적인 방법으로 대답한다. 양자 세계에서 입자는 동시에 파동이기 때문에, 물리학자는 입자의 상태를 기술할 때 위치나 속도보다는 ‘파동벡터’라는 개념을 이용한다.
파동벡터 공간은 우리 눈으로는 볼 수 없는 수학적, 추상적인 공간이다. 3차원 고체가 있다면 이 파동벡터가 존재하는 수학적 공간 역시 3차원이다. 하나의 전자라고 생각했던 것이 이 3차원 파동벡터 공간으로 들어와 보면, 여기저기에 흩어져 존재한다. 파동벡터 공간의 특정한 지점 A에서는 전자가 디랙 입자처럼 행동하고, 지점 B에서는 보통의 전자처럼 행동하는 식이다. 보통의 물질은 파동벡터 공간 어디에서도 전자가 디랙 입자처럼 거동하지 않는다. 하지만 응집물질물리학자들은 대칭성을 이론적으로 고려해 디랙 입자처럼 움직이는 전자가 어떤 물질의 파동벡터 공간에 존재하는지를 알아낼 수 있다.
디랙 입자는 빨간 입자와 파란 입자가 서로 꼭 붙어 있는 꼴이라고 앞서 말했다. 사람도 그렇지만, 입자도 가까이 붙어 있는 것들은 상호작용한다. 두 양자적 입자가 상호작용하면 두 입자의 성질을 모두 띤 ‘중첩된 상태’가 구현된다. 그런데 두 개의 딱 붙어있는 입자가 상호작용하면 질량이 없는 디랙 입자가 전자처럼 질량을 갖는 비상대론적 입자로 바뀐다.
파동벡터 공간은 우리 눈으로는 볼 수 없는 수학적, 추상적인 공간이다. 3차원 고체가 있다면 이 파동벡터가 존재하는 수학적 공간 역시 3차원이다. 하나의 전자라고 생각했던 것이 이 3차원 파동벡터 공간으로 들어와 보면, 여기저기에 흩어져 존재한다. 파동벡터 공간의 특정한 지점 A에서는 전자가 디랙 입자처럼 행동하고, 지점 B에서는 보통의 전자처럼 행동하는 식이다. 보통의 물질은 파동벡터 공간 어디에서도 전자가 디랙 입자처럼 거동하지 않는다. 하지만 응집물질물리학자들은 대칭성을 이론적으로 고려해 디랙 입자처럼 움직이는 전자가 어떤 물질의 파동벡터 공간에 존재하는지를 알아낼 수 있다.
디랙 입자는 빨간 입자와 파란 입자가 서로 꼭 붙어 있는 꼴이라고 앞서 말했다. 사람도 그렇지만, 입자도 가까이 붙어 있는 것들은 상호작용한다. 두 양자적 입자가 상호작용하면 두 입자의 성질을 모두 띤 ‘중첩된 상태’가 구현된다. 그런데 두 개의 딱 붙어있는 입자가 상호작용하면 질량이 없는 디랙 입자가 전자처럼 질량을 갖는 비상대론적 입자로 바뀐다.
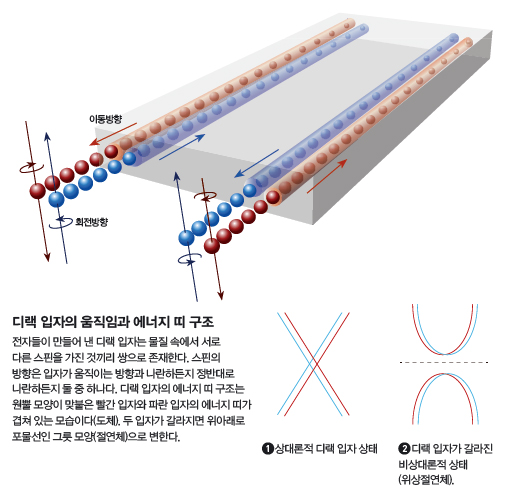
쌍둥이 형제가 집에서 투닥거리지 않고 잘 지내려면 어떻게 해야 할까. “까불면 혼나!”라는 엄마의 무서운 경고가 필요하다. 디랙 입자가, 그러니까 서로 다른 입자 둘이 상호작용하지 않고 질량이 없는 상태로 공존하려면 어떤 거역할 수 없는 원리가 필요하다. 바로 대칭성 원리다. 고체 속에는 무수히 많은 원자가 정렬되어 있다. 고체 속 원자를 배열하는 규칙은 엄격한 대칭성 원리를 따른다. 디랙 물질 이론 연구로 유명한 양범정 서울대 물리천문학부 교수는 이렇게 설명한다. “빨간 입자와 파란 입자가 사는 파동벡터 공간이 회전에 대한 대칭성을 갖는다고 가정합시다. 회전대칭성은, 말하자면 빨간 입자와 파란 입자가 서로 악수할 때 왼손을 사용할지 오른손을 사용할지에 대한 제약을 줍니다. 만약 빨간 입자와 파란 입자 모두 오른손만 사용할 수 있으면, 서로 악수하며 상호작용을 할 수 있어 두 입자 모두 비상대론적 입자로 바뀔 수 있습니다. 반면 빨간 입자는 오른손만 쓰고 파란 입자는 왼손만 쓸 수 있는 경우 두 입자는 서로 악수를 할 수 없기 때문에 상호작용 없이 상대론적 디랙 입자로 남아 있을 수 있습니다.”
만약 이런 대칭성에 의한 보호가 더 이상 작동하지 않아 두 입자가 ‘싸우고 갈라서는’ 상황이 벌어지면 어떻게 될까. 비상대론적 입자가 자리 잡을 수 있는 에너지 구조는 위의 오른쪽 2번 그림처럼 바뀐다. 모든 전자는 아래로 휘어진 ‘에너지 띠’를 차지하고, 위로 휘어진 에너지 상태에는 전자가 하나도 없다. 앞서 말한 모든 아파트 가구에 남자 한명, 여자 한 명씩 들어가 있는 상태, 전기가 통하지 않는 절연체가 된다. 하지만 실망할 필요는 없다. 이 절연체야말로 세상에서 가장 신기한 절연체, 위상절연체가 되니까.
기묘한 절연체를 만든 ‘위상숫자’
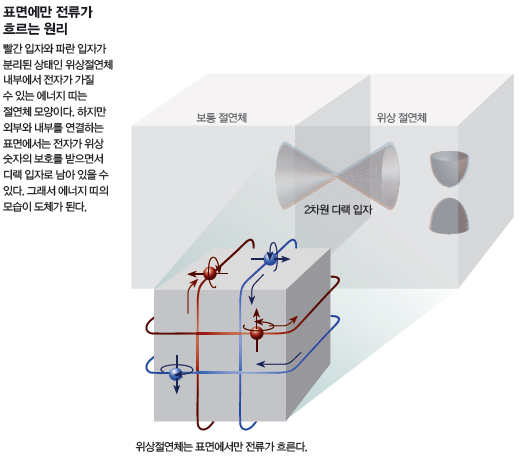
절연체란 물체 양쪽에 전극을 꽂고 전기를 흘리려고 했을 때 전기가 통하지 않는 물질을 말한다. 반면 위상절연체는 전류가 껍질에서만 흐른다. 내부는 절연체, 껍질은 금속인 양자물질이 바로 위상절연체다. 이제 이런 질문을 할 수 있다. 위상절연체의 껍질에서 움직이는 입자는 디랙 입자일까. 물론 그렇다! 3차원 디랙 입자를 깨뜨려서 만든 위상절연체는 본래의 디랙적 존재감을 껍질에 투영해서 2차원 디랙 입자 형태로 유지한다. 마치 악마의 무공을 이기지 못하고 쓰러져 가는 무림 고수가 악마의 무공을 깰 비법을 적은 책과 함께 어린 아들을 머나먼 외지로 보내는 것처럼, 표면으로 ‘추방된’ 2차원 디랙 전자는 무공의 절대 비법 대신 ‘위상숫자’의 보호를 받는다. 절연체의 3차원 파동벡터 공간으로 다시 돌아와서 전자구조를 잘 살펴보면, 어떤 위상숫자를 하나 발견하게 된다. 이 숫자가 짝수면 그 절연체의 표면은 평범하다. 만약 홀수면 그 표면에는 디랙 입자가 ‘반드시’ 존재해야만 한다. 미국 펜실베이니아대 물리및천문학과 찰스케인과 그 동료들의 위대한 발견이다.
분수 전하나 디랙 입자 같은 단어만 열거해 보면 입자물리학자나 우주론 연구자의 사전이 떠오를지 모른다. 하지만 더 이상 그렇지 않다. 응집물질물리학자의 실험실에 놓인 고체 덩어리 속에 이 모든 입자들이 존재한다. 철학적 문제가 있기는 하다.
만약 이런 대칭성에 의한 보호가 더 이상 작동하지 않아 두 입자가 ‘싸우고 갈라서는’ 상황이 벌어지면 어떻게 될까. 비상대론적 입자가 자리 잡을 수 있는 에너지 구조는 위의 오른쪽 2번 그림처럼 바뀐다. 모든 전자는 아래로 휘어진 ‘에너지 띠’를 차지하고, 위로 휘어진 에너지 상태에는 전자가 하나도 없다. 앞서 말한 모든 아파트 가구에 남자 한명, 여자 한 명씩 들어가 있는 상태, 전기가 통하지 않는 절연체가 된다. 하지만 실망할 필요는 없다. 이 절연체야말로 세상에서 가장 신기한 절연체, 위상절연체가 되니까.
기묘한 절연체를 만든 ‘위상숫자’
절연체란 물체 양쪽에 전극을 꽂고 전기를 흘리려고 했을 때 전기가 통하지 않는 물질을 말한다. 반면 위상절연체는 전류가 껍질에서만 흐른다. 내부는 절연체, 껍질은 금속인 양자물질이 바로 위상절연체다. 이제 이런 질문을 할 수 있다. 위상절연체의 껍질에서 움직이는 입자는 디랙 입자일까. 물론 그렇다! 3차원 디랙 입자를 깨뜨려서 만든 위상절연체는 본래의 디랙적 존재감을 껍질에 투영해서 2차원 디랙 입자 형태로 유지한다. 마치 악마의 무공을 이기지 못하고 쓰러져 가는 무림 고수가 악마의 무공을 깰 비법을 적은 책과 함께 어린 아들을 머나먼 외지로 보내는 것처럼, 표면으로 ‘추방된’ 2차원 디랙 전자는 무공의 절대 비법 대신 ‘위상숫자’의 보호를 받는다. 절연체의 3차원 파동벡터 공간으로 다시 돌아와서 전자구조를 잘 살펴보면, 어떤 위상숫자를 하나 발견하게 된다. 이 숫자가 짝수면 그 절연체의 표면은 평범하다. 만약 홀수면 그 표면에는 디랙 입자가 ‘반드시’ 존재해야만 한다. 미국 펜실베이니아대 물리및천문학과 찰스케인과 그 동료들의 위대한 발견이다.
분수 전하나 디랙 입자 같은 단어만 열거해 보면 입자물리학자나 우주론 연구자의 사전이 떠오를지 모른다. 하지만 더 이상 그렇지 않다. 응집물질물리학자의 실험실에 놓인 고체 덩어리 속에 이 모든 입자들이 존재한다. 철학적 문제가 있기는 하다.
고체 덩어리 속엔 전자 밖에 없다. 전자는 분수 전하를 갖고 있지도 않고, 디랙 입자와도 전혀 다르다. 그럼에도 불구하고 전자는 이 모든 것을 흉내 낼 수 있다. 전자만으로 이 모든 입자를 완벽하게 흉내 낼 수 있다면, 과연 우리는 진짜를 찾을 필요가 있을까. 일종의 튜링 시험이다. 모든 면에서 인간과 똑같이 사고하고 대답할 수 있는 기계가 있다면 그걸 굳이 인간이 아니라고 부를 필요가 있을까. 지금까지의 계산용 소자는 전자가 정보를 매개하는 원리에 기반해 왔다. 전자 대신 전자가 매개한 다른 입자가 정보를 매개하는 소자라면 어쩌면 더 좋은 계산기를 우리에게 줄 수 있지 않을까. 21세기 물리학이 풀어야 할 과제다.
한정훈_hanjh@skku.edu http://manybody.skku.edu
성균관대 물리학과에서 다체계 이론을 연구하고 있다. 자성체에 존재하는 스커미온을 예측하는 데 기여했다. 최근에는 텐서 그물망으로 표현되는 양자 상태를 연구하고 있다.
성균관대 물리학과에서 다체계 이론을 연구하고 있다. 자성체에 존재하는 스커미온을 예측하는 데 기여했다. 최근에는 텐서 그물망으로 표현되는 양자 상태를 연구하고 있다.
+더 읽을거리
in 과학동아 31년 기사 디라이브러리(정기독자 무료)
‘‘기묘한’ 2차원 세계를 설명한 개척자들’(2016.11)
dl.dongascience.com/magazine/view/S201611N028
in 과학동아 31년 기사 디라이브러리(정기독자 무료)
‘‘기묘한’ 2차원 세계를 설명한 개척자들’(2016.11)
dl.dongascience.com/magazine/view/S201611N028