d라이브러리 2014년 08월 과학동아

맥스웰이 전기와 자기에 관련된모든 지식을 통합해 만든 ‘맥스웰방정식’은 대칭성을 띠고 있다는점에서 수학자들을 매료시켰다.

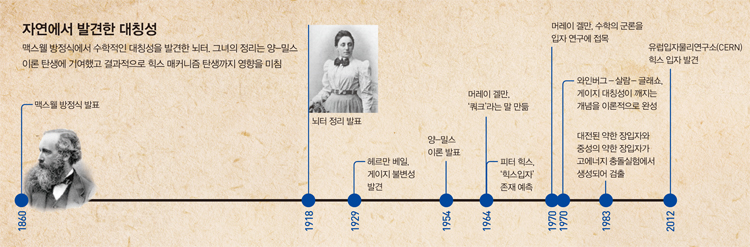
1860년대 영국에서 앞으로 수많은 이론의 밑거름이 될 아름다운 방정식이 만들어집니다. 물리학자 제임스 클러크 맥스웰이 전기와 자기에 관련된 모든 지식을 통 합해 만든 ‘맥스웰 방정식’입니다. 여러 가지 물리학 방정식을 하나로 통합했다는 것도 중요하지만, 맥스웰 방정식에는 수학자들을 매료시킨 특별한 점이 있었습니다. 바로 ‘대칭성’입니다.

대칭성이란 어떤 조작에 대해 변화가 없는 성질을 말합니다. 사람 몸의 외형은 대략 좌우대칭입니다. 좌우를 바꿔도 큰 차이가 없지요. 공은 대칭성이 매우 높아서 어느 방향으로 굴려보아도 항상 똑같은 모습입니다.

대칭은 아름다울 뿐 아니라 수학적, 물리적으로도 중요한 의미를 가지고 있습니 다(과학동아 2014년 1월호 ‘미스터리 입자 헌터’ 참조).

대칭의 아름다움을 찾아낸 수

1918년 독일의 수학자 에미 뇌터는 전하와 에너지처럼 보존되는 물리량이 있을 때, 대칭이 깊은 관계가 있다는 사실을 발견합니다. 그녀는 모든 물리량 보존에는 그것과 관련된 대칭이 존재한다는 사실을 밝혀내지요.

뇌터의 정리에 살이 붙고 붙어 1954년 중요한 이론이 발표됩니다. 미국 시카고대에서 이론물리학을 연구하던 중국인 양전닝과 미국인 로버트 밀스는 뇌터의 정리에 역도 성립한다는 사실을 알고 있었습니다. 두 사람은 물리적 힘에 대한 대칭을 찾았으니 무언가 보존되는 물리량이 있을 것이라고 추정했습니다. 두 사람은 ‘아이소스핀’ 이라는 이름을 가진 입자의 게이지 대칭과 장을 결합한 양-밀스 이론을 발표합니다.

두 젊은 학자가 만든 이론은 오늘날 입자와 기본 힘을 이해하는 데 중요한 버팀목역할을 합니다. 우선 이들 덕분에 고전전자 기학과 양자역학이 합쳐지면서 통일장 이론으로 발전했습니다. 또한 핵을 이루는 두 힘인 강력과 약력을 설명하는 데 큰 도움이 됐습니다. 마지막으로 아직 해결되지 않은 문제이지만, 이 방정식으로부터 나온 질량간극 가설은 전자 등의 질량이 0이 될 수 없는 근거로 사용되고 있습니다.

오늘날 그들의 연구는 표준모형의 핵심 토대를 이루고 있습니다. 하지만 당시만 해도 두 사람은 물리학에 미칠 거대한 충격 을 예견하지 못했습니다. 단지 ‘연구결과의 수학적 아름다움에 기뻐했다’는 기록만 남아있습니다.

가속기 안에 수학이 돌고 있다

양-밀스 이론은 수학적인 아이디어들이 더해지면서 더욱 발전했습니다. 필즈상을 받은 수학자 마이클 아티야는 1970년 대에 양-밀스 이론을 광범위하게 일반화시켰지요. 쿼크라는 말을 만든 머레이 겔 만은 대칭의 수와 종류를 계산하는 수학의 ‘군론(Group Theory)’을 입자 연구에 접목시킵니다. 마침내 입자물리학은 ‘대칭 깨짐’을 이용해 질량을 부여하는 입자가 있다는 사실도 밝혀냅니다.

자연에는 수학적인 대칭이 존재하고, 그 대칭이 깨질 때 질량이 발생한다. 게이지 대칭성이 깨지면서 질량이 발생하는‘힉스 메커니즘’은 그 부산물이라고 할 수 있는 ‘힉스 입자’가 발견되면서 증명됐다.

자연에는 수학적인 대칭이 존재하고, 그 대칭이 깨질 때 질량이 발생한다. 게이지 대칭성이 깨지면서 질량이 발생하는‘힉스 메커니즘’은 그 부산물이라고 할 수 있는 ‘힉스 입자’가 발견되면서 증명됐다.

영국 에든버러대의 피터 힉스를 비롯한 여러 이론물리학자들은 이론상의 대칭을 유지하면서도 실제 대칭이 사라지면 입자에 질량을 부여할 수 있다는 점을 깨닫습 니다. 여기서 물체에 질량을 준다는 힉스 메커니즘이 탄생했습니다. 모두 알다시피 2012년 힉스 입자가 증명됐지요.

아직 기본입자에 대한 의문은 많이 남아있습니다. 많은 물리학자들이 가속기를 통해 입자의 물리적 현상을 관측하고 있는 이유지요. 수학은 물리학의 최전선에서 과학자들의 눈과 손이 되어 주고 있습 니다.

자연에서 발견한 대칭성- 맥스웰 방정식에서 수학적인 대칭성을 발견한 뇌터. 그녀의 정리는 양-밀스이론 탄생에 기여했고 결과적으로 힉스 매커니즘 탄생까지 영향을 미침1860맥스웰 방정식 발표1918뇌터 정리 발표1929헤르만 베일,게이지 불변성발견1954양-밀스이론 발표1964머레이 겔만,‘쿼크’라는 말 만듦 피터 힉스,‘힉스입자’존재 예측

자연에서 발견한 대칭성- 맥스웰 방정식에서 수학적인 대칭성을 발견한 뇌터. 그녀의 정리는 양-밀스이론 탄생에 기여했고 결과적으로 힉스 매커니즘 탄생까지 영향을 미침1860맥스웰 방정식 발표1918뇌터 정리 발표1929헤르만 베일,게이지 불변성발견1954양-밀스이론 발표1964머레이 겔만,‘쿼크’라는 말 만듦 피터 힉스,‘힉스입자’존재 예측

수 : 소수 = 물체 : 기본입자?

“수가 결국은 소수로 분해되고 더는 분해되지 않는다는 사실은, 자연의 구성 요소를 이해하려는 우리의 시도에서 아주 유사한 패턴이 되풀이되리라는 일종의 종교적 신념을 갖게 한다.”

세계적인 수학자 김민형 옥스퍼드대 교수가 저서 ‘소수 공상’에서 밝힌 견해다. 유사 이래 수학과 과학은 늘 함께 발전했다. 소수는 더 이상 나눠지지 않는 수로, 수에 얽힌 많은 비밀을 품고 있다. 수와 소수의 관계를 생각하다보면 결국 자연스레 우주를 이루는 근본 물질에 대한 의문을 품게 된다. 셀 수 없이 많은 과학자가 근본 물질을 찾으려고 도전했다가 실패했지만 아직도 포기하지 않는 이유가 여기에 있지 않을까, 김 교수는 조심스레 추측해본다. 그런데 그는 책 말미에 재미있는 반전을 숨겨놓았다. 소수가 쪼개지지 않는다는 생각이 틀렸다는 것. 과학자들이 이 글을 보면 어떤 생각을 할까.

d라이브러리

❹ 힉스입자 - 수학적 대칭이 깨지면 질량이 생겨난다