d라이브러리

추석이 느지막이 찾아온 올해는 어느 때보다도 과일과 곡식이 풍성하다. 차례 상을 차리기 위해 시장에 들르면 피라미드처럼 보기 좋게 쌓여 있는 사과나 배를 볼 수 있다. 열과 행을 맞춰 서 있는 군인들처럼 맨 밑에 사과를 일렬로 깔아놓은 뒤 그 위로 사과 사이의 움푹 들어간 곳에 두 번째 층을 쌓고 또 그 위로 움푹 들어간 곳에 세 번째 층을 쌓는 방식이다.

사실 상인들은 수천 년 전부터 둥근 과일을 이런 식으로 쌓아놓고 손님을 맞았다. 천체의 운행을 설명한 ‘케플러의 법칙’으로 잘 알려진 독일의 천문학자 요하네스 케플러는 이런 식으로 과일을 쌓는 게 가장 효율적인 방식, 즉 주어진 공간에서 과일을 가장 많이 쌓는 방식이라고 주장했다. 이를 ‘케플러의 가설’이라고 부른다. 케플러의 가설은 그 뒤 400여 년이 지난 1998년에야 옳은 것으로 증명됐다.

케플러 가설, 컴퓨터 동원해 증명

사실 케플러와 그의 영국인 친구는 1600년 경에 크기가 같은 대포알(당시의 대포알은 지금과 달리 공처럼 생겼다)을 어떻게 쌓아야 가장 효율적인지 이야기했는데, 케플러는 시장 상인들이 과일을 쌓듯 쌓는 방식이 가장 효율적이라고 주장했다.

케플러의 주장이 수학적으로 모양새를 갖추려면 여러 관찰이 필요하다. 먼저 빽빽한 정도를 어떻게 측정하는지부터 결정해야 한다. 예를 들어 공간이 아니라 사각형 평면에서 크기가 같은 원을 조밀하게 배치하는 방법을 생각해보자. 먼저 평면을 정사각형 격자로 나누고 지름이 한 변의 길이와 같은 원을 중심이 격자의 교차점에 오게 채워보자.

이 경우 원이 차지하는 부분은 평면 전체 넓이의 78.5% 정도다. 그러나 평면을 정삼각형 격자로 나누고지름이 한 변의 길이와 같은 원을 중심이 격자의 교차점에 오게 배치하면 그냥 봐도 더 빽빽하게 채워졌음을 알 수 있다. 이때 원이 차지하는 부분은 평면 전체 넓이의 90.7% 정도로 정사각형 격자보다 효율이 높다. 만일 사각형 평면의 크기를 무한히 크게 하면



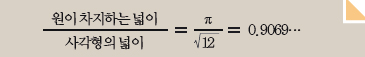
이 나온다.



이제 다시 3차원 공간으로 돌아가서 케플러의 주장처럼 과일 쌓기를 하면



이 나온다. 이 숫자들을 ‘각 채우기 방식의 밀도’라고 부른다. 케플러 방식은 대포알 같은 공이 전체 공간의 74%를 채운다. 여기서 따져봐야 할 것이 하나 더 있다. 지금까지 본 사례는 모두 규칙적으로 채운방식이지만, 규칙이 없게 채우는 방식도 허용하면 어떤 창고에서는 과일 쌓기보다 더 빽빽하게 채우는 방법이 있을 수도 있다.

물론 케플러의 가설이 옳다면 창고의 크기가 무한히 클 때 결국 과일 쌓기가 가장 효율적인 방식일 것이다. 즉 불규칙하게 채워서는 어떻게 해도 이보다는 효율이 낮다는 뜻이다. 실제로 공을 맘대로 채우고 흔들거나 꽉꽉 눌러주면 보통 전체 공간의 64% 정도만 채워진다.

규칙이 있게 공을 채우는 경우 케플러의 과일 쌓기가 가장 효율적이라는 사실은 1800년경에 독일의 수학자 가우스가 증명했다. 불규칙하게 쌓는 경우를 포함하더라도 케플러의 과일 쌓기가 가장 효율적이라는 사실은 1998년에 미국 미시간대의 수학자 토머스 헤일즈가 증명했다.



헤일즈의 증명은 250쪽에 이르는 방대한 논문과 3기가바이트(GB, 1GB=109B) 분량의 프로그램과 계산결과로 이뤄져 있다. 논문에서는 먼저 “만일 규칙이 없는 효율적인(케플러의 가설보다 더 잘채우는) 방식이 있다면 그것은 여차여차한 수천 가지 중 하나다”라
는 사실을 보통의 수학 논문처럼 증명했다.

그리고 이 수천 가지에 대해 부피 비를 구하는 컴퓨터 프로그램을 실행해 그것들 모두가
케플러의 방식보다 효율적이지 않다는 사실을 계산했다. 이로써 증명 끝(QED). 하지만 누군가는 프로그램에 오류가 없고, 컴퓨터 하드웨어에 오류가 없고, 입력과 출력에 오류가 없다는 점을 확인해야 한다.

‘수학연보(Annals of Mathematics)’라는 저명한 수학 학술지에서 그 작업에 도전했는데, 12명의 심사위원이 6년에 걸쳐서 심사한 뒤 마침내 2005년 헤일즈의 논문을 출판했다. 보통 수학 논문에는 심사위원이 많으면 3명 정도가 참여한다. 참고로 페르마의 마지막 정리를 증명한 것으로 유명한 영국의 수학자 앤드루 와일즈의 논문에는 6명의 심사위원이 참여했다.

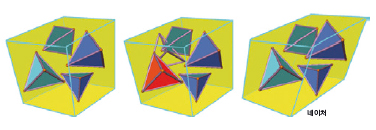
한편 공 모양이 아니라 다른 형태이면 어떤가 하는 문제도 흥미롭다. 예를 들어 물질을 이루는 분자의 모양은 대부분 공 모양이 아니기 때문이다. 사실 이런 경우는 케플러의 문제보다도 더 어렵다. 과학저널 ‘네이처’ 8월 13일자는 크기가 같은 정사면체를 가장 빽빽하게 쌓은 세계 신기록을 표지 논문으로 다뤘다. 미국 프린스턴대 화학과 살바토레 토르콰토 교수와 기계공학과 대학원생인 양 지아오가 역시 컴퓨터 시뮬레이션을 통해 그 방법을 찾아냈다.

한상근 교수는 미국 오하이오주립대에서 박사학위를 받고 1989년 KAIST에 부임했다. 정수론과 그 응용인 암호학, 정보학 분야를 연구하고 있다. 1992년 조선시대 수학자 최석정의 저서‘구수략’을 접하고 이듬해 ‘최석정과 그의 마방진’이라는 논문을 써 최석정이 조합론 분야의 원조임을 알리는 데 기여했다.