d라이브러리

Q 오른쪽 그림처럼 아홉 개의 점이 가로 세로 3개씩 정사각형 모양을 이루고 있다. 연필을 떼지 않고 직선 4개를 그어 모든 점을 지나게 하라. 단 모든 직선은 점의 중앙을 지나야 한다.

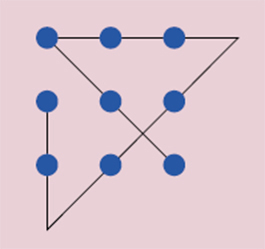
A 아래 그림과 같이 그으면 된다.
 

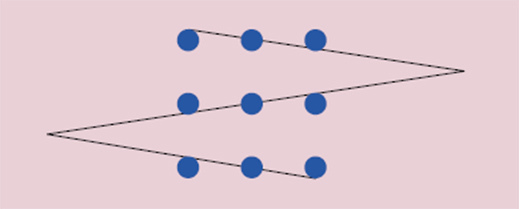
이 문제는 직선의 개수를 3개로 바꿔 약간은 장난스럽게 변형한 형태로도 잘 알려져 있다. 상식적으로는 불가능하지만 점이 꽤 뚱뚱(?) 하다는 사실에 주목하면 아래 그림과 같은 방법으로 직선을 그을 수 있다.
 

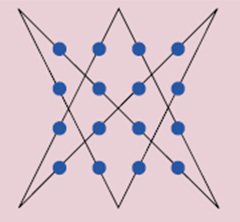
이 문제는 특별한 지식이 필요하지 않으면서도 결과가 주는 대칭의 아름다움 때문에 많은 사람들이 점의 개수를 바꿔가며 여러 형태를 만들었다. 그 중 몇 개를 나열하면 다음과 같다. 지면상 풀이를 하나만 실었지만 대부분 전혀 다른 풀이가 여러개 존재한다.

 

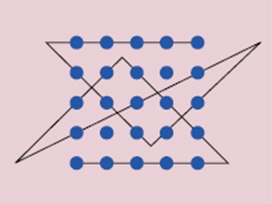
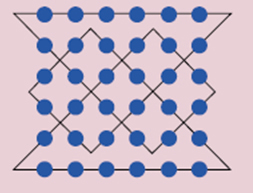
사람들은 단순히 퍼즐의 답을 구하는 것만으로 만족하지 않고, 이런 결과로부터 다양한 예상을 제시했다. 이들 가운데는 수학과 관계가 없는 사람도 많은데, 한 예로 이 분야에 크게 공헌한 언어학자 미하엘 시사우를 들 수 있다.

n×n으로 배열된 점을 한글 자음 ‘ㄹ’ 모양으로 (2n-1)개의 직선을 연결한 것을 ‘자명한 해’라고 하자. 지금까지 얻은 결과에 따르면 'ㄹ' 모양을 만드는데 필요한 직선의 최소 개수는 자명한 해보다 하나 작은 (2n-2)개다.

(2n-2)개의 직선을 그을 수 있는 알고리즘은 여러 사람이 발견했다. 더 적은 수의 직선으로 모든 점을 지나게 할 수 있는 n이 존재할까? 아마 그렇지 않을 것이라고 예상하지만 아직 아무도 증명하지 못하고 있다.

또 n이 짝수인 경우 (2n-2)개의 직선을 그릴 때 같은 점에서 시작해 같은 점에서 끝나면서도 모든 점을 꼭 한 번만 지나도록 할 수 있을 것이라고 예상하고 있지만 이 역시 아직 증명되지 않았다. 자, 여러분이 한번?

지난달 정답_ 첫 번째 나그네 7개, 두 번째 나그네 1개