d라이브러리

크기는 다르지만 모양은 같은 ‘닮음’. 이 성질은 다양한 분야에서 쓰인다. 건축가는 설계한 건축물을 작은 모형으로 미리 만들어본다. 영화 촬영에는 실물을 축소한 세트가 이용된다.

하지만 실생활에서 닮음이 가장 널리 이용되는 경우는 복사기를 꼽을 수 있다. 이를 이용해 우리는 쉽게 원본이 되는 그림이나 글을 축소·확대 가능하다. 그렇다면 복사기가 발명되기 전에는 그림이나 사물을 축소하거나 확대하는 일이 불가능한 것이었을까.

인간은 수세기 전부터 팬터그래프라는 간단한 도구로 그림이나 도형을 확대·축소할 수 있었다. 이를 이용해 원본을 손상시키지 않고 크기만 일정한 비율로 줄이거나 늘려 그릴 수 있다. 팬터그래프는 제도하는 사람이 설계도나 지도를 축소하거나 확대할 때, 또는 세밀화법을 전문으로 하는 예술가가 작품을 더 세밀하게 하기 위해 사용한다. 르네상스 시대를 대표하는 천재 레오나르도 다빈치는 자신의 그림을 복사하는데 이를 이용했다고 한다.
 

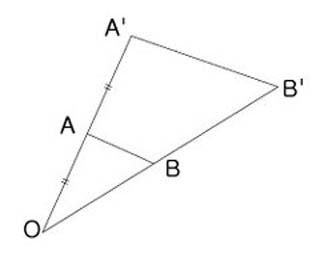
팬터그래프는 수학의 닮음 성질을 그대로 이용한 도구다. 두 삼각형 △OAB와 △OA´B´가 있다. 이 두 삼각형은 한개의 꼭지점 O를 공유한다. 그리고 선분 $\overline{OA}$와$\overline{OA}$´, 그리고 선분 $\overline{OB}$와 $\overline{OB}$´은 각각 같은 선분 위에 있고, 선분 $\overline{AB}$, $\overline{A´B´}$은 평행이다. 그렇다면 이 두 삼각형은 어떤 관계일까. 한개의 꼭지점 O를 공유하고 있기 때문에 ∠AOB와 ∠A´OB´가 같다. 선분 $\overline{AB}$, $\overline{A´B´}$가 평행하므로 ∠OAB와 ∠OA´B´가 같다. 따라서 두 삼각형은 서로 닮았다. 이때 $\overline{OA}$ : $\overline{OA}$´ = 1 : 2라면 △OAB와 △OA´B´의 닮음비는 1 : 2이다.


막대 4개로 만드는 닮은꼴

두개의 닮은 삼각형이 팬터그래프에 적용됐다. 팬터그래프는 4개 막대가 2개씩 서로 평행하게 연결돼 있고, 이들은 관절처럼 움직인다. 이 구조를 잘 살펴보면 2개의 닮은 삼각형을 찾을 수 있다. 막대의 끝과 막대들이 만나는 관절 부위에 점을 찍는다. 이 점들을 연결해보면 바로 두개의 닮은 삼각형이 그려진다.
 

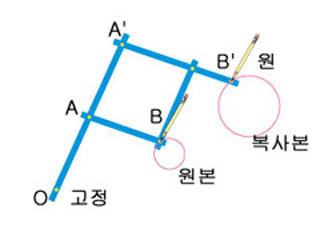
팬터그래프의 사용법은 어떨까. O에 해당하는 지점을 어느 한곳에 고정시킨다. 그리고 B와 B´에 구멍을 뚫는다. B´에는 펜을 꼽아 고정시키고, B 지점은 원본 그림을 따라 이동할 수 있는 펜을 놓는 위치다. 이제 원본을 따라 B의 펜을 이동시킨다. 그러면 B´의 펜이 함께 이동하면서 원본과 같으면서 일정한 비율로 확대된 그림을 그려간다. 만약 2배로 확대하고 싶다면 1 : 2인 닮은 삼각형이 팬터그래프에 숨어 있으면 된다.

팬터그래프로는 닮은 도형을 그릴 수 있을 뿐만 아니라 어떤 모양에서의 비례를 확인할 수 있다. 닮음비 중에 가장 유명한 황금비를 확인할 수 있는 팬터그래프를 만들어보자.

황금비는 약 2천3백년 전 그리스 사람들이 이름 붙였다. 중세 사람들은 이 비를 신의 의지로 생각해 ‘신의 비’라고 불렀다. 흔히 황금비를 ‘피’(phi)라고 부르는 것은 그리스의 유명한 조각가였던 피디아스(phidias) 때문인데, 이 황금비는 파르테논 신전의 기둥들 윗부분에 있는 조각품을 포함해 그의 여러 작품들 속에 풍부하게 나타나고 있다.

황금비라는 이름은 귀하다는 의미와 함께 변하지 않는다는 황금의 성질에 빗대어 붙여졌다. 변하지 않는 비라는 말은 어떤 선분을 자를 때 황금비로 자르면 분할된 두부분 중 작은 것의 큰 것에 대한 비례가 큰 것에 대한 전체 비와 항상 같게 된다는 것을 뜻한다. 황금비는 무리수로 정확한 값이 $\frac{(1+\sqrt{5})}{2}$ 이며, 보통 소수점 셋째자리까지 표현해서 1.618이다.

황금비는 자연에서 쉽게 찾을 수 있다. 식물에는 무궁화, 야생 제라늄, 노란 바이올렛 등이 있으며 앵무조개와 같은 해양동물에서도 황금비를 발견할 수 있다. 앵무조개는 껍질이 아름다운 소용돌이 무늬의 나선 모양이다. 이 나선무늬를 가로와 세로로 접선을 그려본다. 이때 접선 길이의 관계가 황금비를 이룬다.

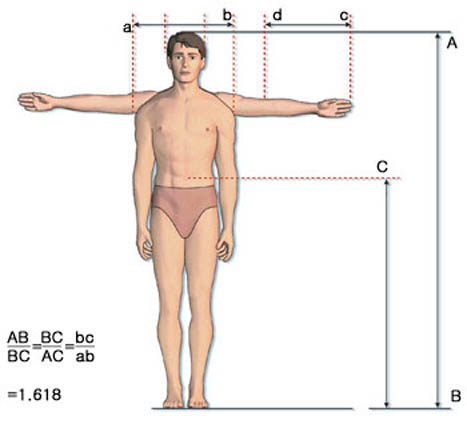
또 우리 몸에서도 황금비를 찾아볼 수 있다. 건축가 르 꼬르뷔제는 인간의 몸 분할을 연구해 배꼽이 몸 전체를 황금분할로 나누고, 목이 윗부분을, 무릎이 아랫부분을 황금분할한다는 점을 알아냈다. 또 어깨 폭에 대한 팔 길이에 비도 황금비를 이룬다.