d라이브러리

확장수

원시인들은 하나 둘 셋 많다로 밖에는 수를 셈할줄 몰랐다고 한다. 그 후에 인간의 두뇌가 발달함에 따라 자연수(natural numbers) 를 알게되었을 것이다. 또한 음수(negative numbers) 와 0(zero)의 개념도 도입되었다.

그 세 가지를 합쳐서 만든 정수(whole numbers) 가 발전되고 이어 소수(decimal numbers) 를 포함하는 유리수(rational numbers) 가 탄생했다. 또 원주율 삼각함수의 값 등을 포함한 비순환 무한소수와 제곱근을 포함하는 무리수(irrational numbers) 가 합쳐져서 실수(real numbers) 라는 수체계가 되었다.

그 실수체계에 허수(imaginary numbers) 를 더해서 현재까지 가장 큰 수체계라고 알려진 복소수(complex numbers) 가 된 것이다.

"그럼, 그보다 더 큰 수체계는 없을까?"하는 의문이 나의 뇌리를 스쳐갔다. 학교 교실에 남아서 자율학습을 하던중에 갑자기 떠오른 것이었다.

나는 이 의문의 해답을 찾는 작업에 곧 착수했다. 우선 그 수체계의 기호와 더불어 이름을 적었다. 허수의 기호 'i'는imaginary numbers의 첫자를 따왔다는 점에서 힌트를 얻어 'expanded numbers'(확장수)의 첫글자인 e를 기호로 쓰기로 했다. 단, 수식의 계산등에서 e라는 문자가 미지수 내지는 어떤 정수(定數)로 쓰일 수도 있으므로 그 밑에 점(dot)을 찍어'(ẹ)'(e dot)라고 쓰고 그렇게 읽기로 하였다.

다음엔 ẹ= $\sqrt{-i}$, 즉 ẹ²= -i로 '정의'했다. 그리고 ${ẹ}^{0}$ ${ẹ}^{1}$ ${ẹ}^{2}$ ${ẹ}^{3}$ ${ẹ}^{4}$ ${ẹ}^{5}$ …등을 계산해 보았다. 뭔가 되는것 같아서 수학선생님께 이 사실을 말씀드렸다. 선생님은 내게 사칙연산 교환 결합 배분법칙 인수분해 등을 해 보라고 충고하셨다.

인수분해는 수학 교과서 등에 있는, "다음 정식을 복소수 범위까지 인수분해 하시오"하는 문제를 "…을 확장수 범위까지 인수분해 하시오"로 고쳐서 풀어 보았다. 그 결과 모두 적용되었다.

 ẹ= $\sqrt{i}$인 경우에는 확장수의 개념이 필요없으나, 현 단계에선  ẹ= $\sqrt{-i}$일 경우에 확장수가 성립한다. 조금 더 두고 연구해 보아야 하겠지만, 앞으로는 수학책에, "가장 큰 수체계는 확장수이다"라고 나올른지도 모를 일이다.

시공좌표

만일 어떤 물체가 직선상으로 움직일때 이동한 자취를 표시하려면 수직선이 필요하다(1차원). 그러나 평면위를 왔다갔다할 때는 좌표평면 이 필요하다(2차원). 또 3차원적(입체적)운동을 할 때는 공간좌표 가 필요하다

그러나 한 가지 빠진 것이 있다. 만일 그냥 물체가 이동한 좌표상의 위치들이 자취만을 표시한다면 문제가 없겠지만, 물리에서 특히 역학에서, 단위시간당 이동한 위치 및 거리를, 또는 일정 거리를 이동할 때의 위치를 표시하려고 한다면 한 차원씩이 더 필요하기 때문이다.

이를 표시하기 위해 나는 시공(時空)좌표(the time-space co-ordinates)를 만들었다. 이 시공좌표는 4차원적인 좌표계다. 말하자면 공간좌표(x축-y축-z축)를 새로 설정한 시간축(t축)에 따라 쭉 늘어 놓음으로써 형성된다.

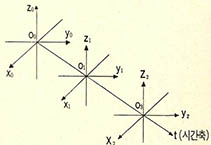
시공좌표의 기본형태는 (그림1)과 같이 된다.
즉 공간좌표 ${x}_{n}$-${y}_{n}$-${z}_{n}$을 시간축t의 n점을 따라 이동시키는 것이다. 여기서 n은 t축이 가지는 값이다.
더 자세히 설명을 해보면, t축의 ${x}_{0}$-${y}_{0}$-${z}_{0}$은 물체의 위치 및 시간을 측정하기 시작하였을 때이다. 또 t축의 값이 1,2,3…으로 변함에 따라 ${x}_{1}$-${y}_{1}$-${z}_{1}$, ${x}_{2}$-${y}_{2}$-${z}_{2}$, ${x}_{3}$-${y}_{3}$-${z}_{3}$…으로 변하게 된다. 물론 각각의 공간좌표에 ${P}_{0}$,${P}_{1}$,${P}_{2}$,${P}_{3}$…의 값을 표시해 준다.

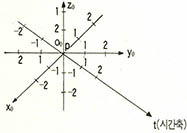
실제로 시공좌표를 작성해 보자.
우선 공간좌표 ${x}_{0}$-${y}_{0}$-${z}_{0}$와 시간축 t를 설정한다. (그림2) 다음 ${x}_{0}$축, ${y}_{0}$축, ${z}_{0}$축과 t축에 눈금을 매기고 P의 점을 찍는다.(물론 여기서 P의 점은 ${O}_{0}$의 점과 일치한다. 즉, t축이 갖는 값이 0이므로, 물체 P의 관찰을 시작했음을 나타낸다.) 그리고나서 t축의 값이 1,3,6이 되는 곳에 각각 ${x}_{1}$-${y}_{1}$-${z}_{1}$(원점은 ${O}_{1}$), ${x}_{3}$-${y}_{3}$-${z}_{3}$(원점은 ${O}_{3}$), ${x}_{6}$-${y}_{6}$-${z}_{6}$(원점은 ${O}_{6}$)의 공간좌표를 잡고서 P',P",P'"의 점을 표시한다.

이제까지 살펴본 시공(時空)좌표라는 새로운 개념의 도입에 의해 우리는 4차원을 평면(2차원)인 종이위에 표시할수 있게 될지도 모른다. 물론 아직 완전한 것은 아니다. 예를 들면 측정하는 물체의 연속적인 위치를 선으로 표시하고자 할 때 시공좌표는 쓸모가 적어지게 된다. 만일 그 물체가 아주 불규칙적인 운동을 해서(예로 브라운 운동) 한 번 지나간 곳에 다시 온다면, 종래의 공간좌표만으로는 그 점에 오기 전의 위치와 후의 위치등을 정확히 알 수가 없다. 물론 시공좌표로 그런 것을 간단히 알 수 있으나, 한 점에서 다른 점으로 이동하는데 걸린 시간은 알지 못하게 된다.

그러므로 나는 이 글을 읽으시는 분들중의 어느 한 분이 이 시공좌표를 좀 더 개량해 주었으면 한다. 마치 '네이피어'에 의해 발견되고 '브릭스'에 의해 개량 log(로가리즘)처럼.
 

독창성과 진지한 태도에 흐뭇함 느껴

나는 이군의 글을 읽고 한마디로 우리나라에도 밝은 미래를 기대할 수 있다는 흐뭇함을 느꼈다는 것이 솔직한 심정이다.
그것은 첫째로, 요즈음과 같은 치열한 입시 경쟁속에서도 입시문제와는 직접적으로 관련성이 없는 수학문제에 깊은 관심을 가지고 몰두했다는 점에 진정으로 깊은 감명을 받았다. 이군은 넓은 시야도 있었거니와 또한 마음의 여유도 있다고 생각된다. 우리의 사회풍토에서는 기성세대에 있어서도 그 같은 여유를 찾아 보기 어려운 것이 현실이다.

그리고 둘째로는, 무엇보다도 그의 창의적이고 학구적인 태도에 높은 찬사를 보내고자 한다. 비록 그의 착상이 수학에서 볼 때 새로운 발전에까지 이르지는 못하였으나, 그의 문제에 대한 창의성있는 시도는 참으로 가상한 것이었다.

우리나라의 교육제도에서 자주 지적된 점이 암기위주의 입시를 위한 교육임은 너무도 잘 알고 있다. 즉 비창의적인 교육이다. 그러기때문에 이군과 같은 독창성이 돋보이는 학구적인 진지한 태도는 참으로 값진 것이다.

이군의 글은 두 가지 문제를 다루고 있다. 이 두 문제를 지면의 범위내에서 간단히 평가하기로 한다. 첫째의 '확장수'는 이군의 독창적인 문제의 통찰력을 돋보이게 한다고 말하고 싶다. 이군이 지적한대로 수의 체계가 자연수 정수 유리수 실수체계로부터 복소수체계로 확정되었다. 그런데 이 확장은 ${x}^{2}$=-1인 x가 실수로는 존재하지 않기 때문에 이 x를 i로 나타내는 것이다. 즉 실수체계에 i를 첨가한 수체계가 복소수체계이다. 이군은 이와같은 확장의 방법을 모방해서 복소수체계에서 다시 ẹ²= -i인 ẹ를 새로 도입시키고, 복소수체계를 확정시켰다고 하였다.

이군의 이같은 확장은 첫째로 복소수체계를 보다 더 큰 체계로 확장할 필요성이 없다는 점과, 둘째로, 이군이 지적한 ẹ라는 수가 복소수에 지나지 않는다는 점을 지적한다. 따라서 ẹ가 복소수에 불과하기 때문에 확장수가 될 수 없다는 점이다. 고등학교 2학년생으로는 ẹ=$\sqrt{-1}$ 가 복소수임을 보이기에는 무리한 문제이다. 이 문제는 이군이 대학교 수학과 2학년 또는 3학년의 함수론의 수준에 이르러서야 깨닫게 될 것이다.

이군이 다룬 둘째의 문제인 시공좌표에서도 그의 창의적인 면을 충분히 엿볼수 있으나 한마디로 타당한 이야기는 아니다. 아무튼 그의 통찰력있는 '그림'등을 보면서 이군이 장차 수학과 같은 창의성을 요구하는 학문에 진학한다면 그의 소질을 발휘할 기회가 반드시 있을 것으로 기대된다.