최대공약수를 구할 때 흔히 사용되는 방법이 유클리드 기하원본에 소개된 호제법이다.놀랍게도 구장산술 첫장에 나오는 단순한 분수 계산의 풀이법에 이런 유클리드 호제법과 동일한 방법이 소개돼 있다.
지난호에서 우리는 ‘구장산술’이 동양 최초의 수학서이면서 후대에 미친 영향이 지대했다는 점을 알게 됐고, 저자인 유휘가 쓴 서문에서도 부분적으로나마 살펴보았다. 사실 어떤 책이 한 문명권의 과학문화를 적어도 2천년 동안이나 지배했다는 사실은 그 자체로서 결코 보통 사건이 아니다. 우리가 지금 하려는 작업은 그 같은 엄청난 영향력의 비밀을 파헤쳐서 그 에너지로 우리의 수학적 사고력을 충전해보자는 것이다.
그러면 이제부터 아홉장으로 이뤄진 이 책의 첫째장을 살펴보자. 첫째장은 ‘방전’(方田)으로 분수 계산과, 평면기하 위주의 도형 넓이 계산을 다루고 있다. 얼핏 봐서는 도저히 오늘날의 중·고등학교 수학 수준에도 미치지 못하는 진부한 내용으로 비춰지기 쉽다.
하지만 그렇지 않다. 첫째장이라고 해서 우리의 수학적 사고력을 북돋아주고 풍요롭게 할 에너지나 자양분이 절대로 모자라지 않다. 여기서는 이런 자양분을 특히 동양의 ‘유클리드 호제법’이라 할 수 있는 ‘상감법’(相感法)과 고리모양의 밭인‘환전’(環田)이라는 두 주제에 초점을 맞춰서 살펴보기로 하겠다.
간단한 약분 설명 속에서 놀라운 발견
구장산술 첫째장인 방전 장의 다섯번째와 여섯번째 문제는 각각 $\frac{12}{18}$와 $\frac{49}{91}$ 을 약분하라는 것이다. 사실 이런 소중한 지면에 언급하기에는 너무나 격이 떨어지는 문제들이라고 할 수 있다. 하지만 이들 속에는 동양의 유클리드 호제법이라 불릴 수 있는 놀라운 방법이 숨어 있다.
일반적으로 우리는 약분 문제에서 최대공약수를 발견하고, 이를 위해서 소인수분해나 유클리드 호제법을 써야 한다는 사실을 알고 있다. 아닌게 아니라 $\frac{49}{91}$ 의 분모와 분자를 소인수분해하면
$\frac{49}{91}$ = $\frac{7·7}{7·13}$ = $\frac{7}{13}$
이라고 계산하게 된다. 그런데 정작 구장산술의 풀이법은 어떻게 돼 있을까.
“약분술(約分術)에 따라서 반으로 나눌 수 있는 것은 반으로 나누면 되고, 반으로 나눠지지 않는 것은 분모·분자의 수를 다른 곳에 놓고, 큰 것에서 작은 것을 빼고 나서, 다시 서로서로 빼주는 일을 되풀이해 그것들의 등수(等數)를 구해 등수로 그것들을 나눈다.”
이 풀이법에서 ‘반으로 나눌 수 있는 것은 반으로 나누면 되고’라고 말한 것은 물론 분모·분자가 짝수인 경우에는 2라는 약수를 활용하면 된다는 뜻이다. 정작 주목할 대목은 ‘반으로 나눠지지 않는’ 경우다. $\frac{49}{91}$ 의 예를 들어보자. 이때 분모가 분자보다 크므로 91에서 49를 빼면 42가 나온다. 그리고 이번에는 49에서 42를 뺀다. 그러면 7이 남는데 이것이 바로 우리가 최대공약수로 알고 있는‘등수’(等數)다. 등수 7로 분모와 분자를 나누면 $\frac{49}{91}$는 $\frac{7}{13}$ 로 약분된다.
놀랍게도 이에 대한 처방전이 정확히 ‘유클리드 호제법’과 일치하는 것이 아닌가! 단지 여기서 최대공약수가 ‘등수’라 지칭하고 있을 뿐이다.
최대공약수가 최대등수
사실 이 방법이 오늘날 흔히 유클리드 호제법이라 지칭되는 이유는 이것의 출처가 유클리드의 ‘기하원본’에 나오는 다음과 같은 두 명제라고 보기 때문이다. 기하원본의 원문을 보자.
[명제 1] 서로 다른 두수를 배열해서, 큰 쪽에서 작은 쪽을 계속 번갈아 빼주다가, 만일 나머지가 그보다 앞선 수를 측정하지(연산하지) 못하고 하나의 숫자(최대공약수)가 남으면, (이로 나눈) 원래의 수들은 서로 소가 된다.
[명제 2] 두수가 서로 소가 아니면, 최대공약수를 구할 수 있다.
기하원본은 명말에 선교사 마테오 리치(Matteo Ricci, 1552-1610)가 중국에 와서 서광계(徐光啓, 1562-1633)와 더불어 처음 여섯권을 번역해 1607년에 펴냈다. 이후 오랫동안 미완성인 채로 남아 있다가 청말인 1857년이 돼서야 영국인 알렉산더 와일리(Alexander Wylie, 1815-1887)가 수학자 이선란(李善蘭, 1811-1882)의 도움을 받아 나머지 작업을 끝마친 것으로 유명하다.
그런데 호제법과 관련된 두 명제는 제7권에 들어있어서 와일리와 이선란이 옮기게 됐다. 그들은 소수(素數)는 ‘무등수’(無等數)로, 그리고 최대공약수는 ‘최대등수’(最大等數)로 각각 옮겼다. 한눈에도 구장산술 약분술의 용례를 그대로 따른 결과임이 분명하다. 이는 고대 동양사회가 유클리드 호제법을 독자적으로 터득하고 있었으며, 이것이 구장산술 약분술의 용어로는 ‘상감법’(相減法, 서로 빼주는 법)에 해당한다는 사실은 알면 알수록 놀랍기만 하다.
그런데 이런 사실은 중국이나 일본에서 쏟아져 나오는 구장산술의 최신 주해서들마저 한결같이 간과했고 필자 역시 최근에 번역을 서두르는 과정에서 이 점에 대한 지적을 빼먹고 말았다. 각국의 구장산술 연구 자체가 이런데 약분술의 의미를 학교에서 제대로 가르친다는 일은 아예 기대조차 하기 어려운 노릇이다.
어떤 이는 21세기에 접어든 마당에 케케묵은 고서를 들춰내서 무엇에 쓰겠느냐고 말할지 모르겠다. 그러나 우리는 뻔한 약분문제로부터도 큰 발견을 얻을 수 있다는 사실을 앞에서 보았다. 고대 동양사회에도 동양의 유클리드 호제법이라 할 수 있는 상감법이 존재했다는 깨달음이 어찌 우리들의 문화적 자긍심과 수학적 사고에 도움이 안되겠는가.
일본 중3 참고서에 등장하는 문제
환전은 고리나 반지 모양의 밭을 말한다. 방전 장 끝부분에 이에 관한 두 문제가 등장하는데, 특기할 만한 점은 두 동심원의 반지름 대신에 원둘레와 이들 사이의 간격을 알려주고 있다는 사실이다. 그중 하나를 살펴보도록 하자.
[문] 지금 고리 모양의 밭이 있는데, 안쪽 둘레가 92보, 바깥쪽 둘레가 1백22보, 둘 사이의 간격이 5보이다. 밭의 넓이는 얼마인가?
[답] 2무 55보2(여기서 ‘무’(畝)는 넓이의 단위로 1무 = 2백40보2이고 ‘보’(步)는 거리의 단위로 1보 = 6자 = 1백82cm이다).
이 문제에 대해 제시된 풀이법은‘안쪽 둘레와 바깥쪽 둘레를 합해서 반으로 나눈 다음, 둘 사이의 간격을 곱하면, 넓이의 보(步)수가 된다’는 것이다. 얼핏 보면 복잡한 암호문 같지만 잘 들여다보면 그렇게 어려운 답은 아니다.
이제 큰 원과 작은 원의 반지름을 각각 r1, r2, 두 원둘레 사이의 간격을 d라고 하자. 물론 두 원둘레 사이 간격 d는 두 반지름의 차가 된다. 그리고 원둘레는 2π에 원의 반지름을 곱하면 되므로, 고리 모양 밭의 바깥쪽 둘레, 즉 큰 원의 둘레는 2πr1이 되고, 밭의 안쪽 둘레, 즉 작은 원의 둘레는 2πr2가 된다.
그러면 우리가 원하는 고리 모양의 밭 넓이 S는 큰 원의 면적에서 작은 원의 면적을 빼면 된다. 즉
S = π(r₁² - r₂²) = π(r₁ - r₂)(r₁ + r₂)
= d·π(r₁ + r₂) = d·π(r₁ + r₂) = d·(πr₁ + πr₂)
이라는 관계가 성립된다. 여기서 간단한 인수분해 공식인 a2 - b2 = (a - b)(a + b)와 두 원둘레 간격 d = r1 - r2를 이용했다. 최종적으로 얻은 고리 모양 밭 넓이를 살펴보면 ‘안쪽 둘레와 바깥쪽 둘레를 합해서 반으로 나눈 다음, 둘 사이의 간격을 곱하면 넓이가 된다’는 풀이법의 공식을 확인할 수 있다.
그런데 이렇게 식을 통한 증명과정 자체는 일본에서 나온 한 참고서를 보면, 중3 수준의 인수분해 응용문제로 분류돼 실려 있다. 그 참고서의 편집자가 과연 구장산술 문제를 활용했는지는 불분명하다. 그러나 아무려면 어떤가. 이 문제만 봐도 구장산술이 오늘날의 중학생에게까지 여전히 훌륭한 교재가 될 수 있음이 드러나는데.
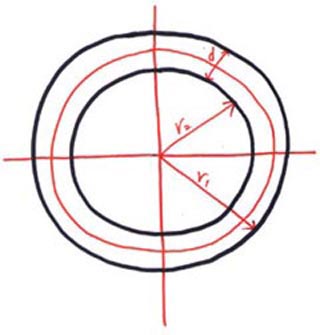
고리 모양과 같은 넓이의 직사각형
여기서 한걸음 더 나아가보자. 고리 모양의 밭을 이루는 두 원의 한가운데를 맴도는 제3의 원을 가정한다. 이 원의 둘레를 l이라고 하자.
그러면 제3의 원에서 반지름은 작은 원의 반지름 r2에 원래 두원 간격 d의 반을 합한 값이 된다. 따라서 제3의 원둘레는
ι = 2π(r₂ + $\frac{d}{2}$) = 2π(r₂ + $\frac{r₁-r₂}{2}$) = 2π$\frac{r₁+r₂}{2}$ = π(r₁ +r₂)
이다. 이런 사실을 이용해 고리 모양의 밭 넓이 S를 다시 나타내면 S=d·l 이 된다.
구장산술의 풀이법이 은근히 강조하려던 포인트는 아마도 고리 모양의 밭 넓이가 바로 가로와 세로가 각각 l과 d인 직사각형의 넓이라는 점이었을 것이다. 고리 모양의 밭 넓이가 직사각형 밭 넓이와 같다는 사실이 재미있지 않은가.
궁금증풀이
Q: ‘유클리드 호제법’이 뭐예요 ?
A: ‘유클리드 호제법’(Euclidean algorithm)은 고교수학의 수학 I을 공부하다보면, 수와 집합이라는 단원에서 만나게 되는, 최대공약수(GCM)를 구하는 방법이랍니다. 호제법을 간단히 말하면 두수의 최대공약수를 구할 때 큰 수에서 작은 수를 나눈 나머지를 잇달아 재활용해 나눗셈을 이어가는 방법이지요. 아직도 잘 모르겠지요. 예를 들어볼까요. 90과 168의 최대공약수를 호제법을 이용해 구해봅시다.
호제법의 풀이과정 속에 정답인 6이 나타나는 사실이 신기하지요. 위의 (a)는 미국의 한 대학교재에서 발견한 것이고, (b)와 (c)는 일본 참고서들에서 찾아낸 계산방식입니다. 같은 호제법을 적용하더라도 방법이 나라와 사람에 따라서 제각각 다를 수 있지요. 그러나 원리나 풀이과정만큼은 모두 같답니다. 이렇게 되는 원리를 간단히 살펴볼까요.
두 자연수 A, B가 있다고 하지요. 이때 A는 B보다 큽니다. A를 B로 나눈다고 할 때 나눈 몫과 나머지가 생기지요. 이를 각각 Q, R이라고 합시다. 그러면 A와 B의 최대공약수가 놀랍게도 B와 R의 최대공약수와도 일치한답니다. 이 관계를 계속해서 이어가는 방법이 바로 호제법입니다. 그림의 예에서는 A = 168, B = 90이고 168을 90으로 나눈 나머지 R = 78이지요. 호제법에 따르면 168과 90의 최대공약수가 90과 78의 최대공약수가 일치합니다. 여기서 이번에는 90을 A로, 78을 B로 사용하면 90을 78로 나눈 나머지 R = 12가 되지요. 다시 78을 A로, 12를 B로 사용해서 똑같은 방식을 계속 적용하다보면 결국 최대공약수 6을 만나게 됩니다.
여기서 한가지 더 짚고 넘어갑시다. 원래 유클리드의 기하원본에 등장하는 호제법에 대한 설명부분에는 ‘큰 수에서 작은 수를 계속 번갈아 빼준다’는 표현이 나온답니다. 하지만 이 사실은 위에서 말했던, ‘큰 수에서 작은 수를 나눈다’는 표현과 같답니다. 왜냐하면 큰 수에서 작은 수를 여러번 빼주는 일은 큰 수에서 작은 수를 나누는 일과 같기 때문입니다. 예를 들어 78에서 12를 6번 빼준 결과가 78을 12로 나눈 나머지인 6과 같지요.
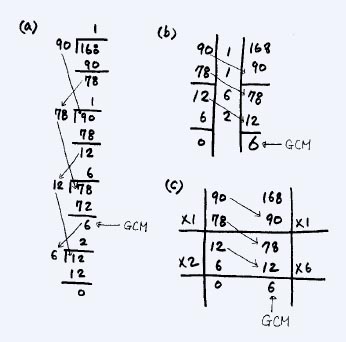
한걸음 더 나아가기
Q: 왜 A와 B의 최대공약수가 B와 R의 최대공약수와 일치하나요?
A: 그러면 유클리드 호제법을 일반적으로 증명해야 하지요.
앞에서 두 자연수 A와 B를 생각했지요(물론 A는 B보다 큽니다). A를 B로 나눈 몫과 나머지를 Q와 R이라고 했고요. 그러면 A = BQ + R이라는 식이 성립하지요. 유클리드 호제법의 원리는 바로 여기서 A와 B의 최대공약수가 B와 R의 최대공약수가 같다는 말이랍니다. 그런데 왜 그럴까요.