d라이브러리

아름다운 선율을 자랑하는 음악과 딱딱한(?) 수학은 전혀 어울리지 않을 것 같아 보인다. 그러나 수학자는 음악의 역사 첫 장부터 등장하며 수학 없이는 음악 이론을 전개할 수 없다.

‘수는 만물을 지배한다’고 주장했던 피타고라스는 음정이 ‘수’의 지배를 받는다는 사실을 발견했다. 음정은 동시에 울리거나 연이어 울리는 두 음의 높이의 간격인데, 일반적으로 ‘도’를 단위로 해서 음계에서 똑같은 단계에 있는 두 음의 음정을 1도, 한 단계 떨어져 있는 두 음의 음정을 2도라 한다. 간격이 한 단계씩 넓어짐에 따라 3도, 4도라 하는데, 8도를 1옥타브라고 부른다.

피타고라스는 장력과 재질이 서로 같은 두 현을 퉁겼을 때 나오는 두 음은 길이의 비가 2 : 1이면 8도, 3 : 2이면, 5도, 4 : 3이면 4도 음정이 난다는 사실을 발견했다. 그리고 현의 길이가 이렇게 간단한 정수의 비로 표현될수록 어울리는 소리가 나고, 복잡할수록 어울리지 않는다는 사실도 발견했다. 실제로 1도, 4도, 5도, 8도 음정만을 완전 어울림 음정이라고 한다. 이렇게 피타고라스의 음정 이론은 서양 음악 이론의 출발점이 되면서 음악과 수학은 밀접한 관계를 맺었다.

로그를 이용

피타고라스의 음정 이론에 따라 음계를 정하는 방법을 순정률(또는 순정조, pure temperament)이라고 한다. 현을 퉁겼을 때, 현의 길이가 짧을수록 진동수는 커지고, 현의 진동수가 클수록 높은 음이 나온다. 즉 음의 높이는 현의 길이에 반비례하고 진동수에 비례한다. 순정률에 따른 C장조 음계에서 각 음에 대응하는 진동수와 인접한 진동수 사이의 비를 보면 음정의 합과 진동수 비의 곱이 멋지게 대응한다는 사실을 발견할 수 있다. 예를 들어 5도 음정과 4도 음정의 경우는 다음과 같다.

음정의 합:5도 + 4도 → 8도
↕ ↕ ↕
진동수의 비의 곱: $\frac{3}{2}$ x $\frac{4}{3}$ = $\frac{2}{1}$

이와 같이 덧셈과 곱셈 사이의 관계가 성립하기 때문에, 곱셈을 덧셈으로 바꾸는 로그가 이런 맥락에서 이용된다.

순정률은 음정을 정수의 비로 간단하게 나타내고 이에 따라 완벽한 화음을 보장한다. 그렇지만 순정률에서는 음정이 일정하지 않다. 똑같은 2도 음정이라도 진동수의 비가 각각 9 : 8, 10 : 9, 16 : 15로 다르기 때문이다. 거의 비슷한 처음 두 가지를 각각 온음이라 하고, 훨씬 작은 마지막 경우를 반음이라고 한다. 그런데 순정률에서는 두 반음의 합이 온음이 되지 않는다는 결정적인 약점이 있다. 즉 반음에 대응하는 진동수의 비인 16/15을 두 번 곱하면 16/15×16/15≒1.138로 온음에 대응하는 진동수의 비 9/8≒1.125 또는 10/9≒1.111보다 커진다. 그래서 C장조를 D장조로 조바꿈을 할 경우 D와 E의 첫째 음정은 진동수의 비가 원래의 9 : 8이 아니라 10 : 9가 되는데, 이 경우에는 차이점을 거의 알 수 없다. 그렇지만 다음 음정은 온음이기 때문에 E와 F 사이의 반음과 F와${F}^{＃}$ 사이의 반음을 더해야 하는데, 음계에 이런 음정은 없다. 이런 문제점은 곡이 진행될수록 더욱 커진다.

순정률은 순수하고 완벽한 화음을 지녔기 때문에, 음높이를 자유롭게 바꿀 수 있는 무반주합창(아 카펠라)이나 현악기의 합주 등에서는 그 화성적 아름다움이 살아나지만, 음높이를 고정시킨 악기(피아노, 관악기 등)에서는 온음의 폭이 고르지 않고 조바꿈이 곤란하다는 등의 문제점이 있다.

1옥타브 속에 숨은 등차, 등비수열

순정률의 문제점을 보완한 방법으로 현재는 건반 악기를 중심으로 해서 1옥타브를 반음씩 12등분한 평균율(equal temperament)이 일반적으로 쓰이고 있다. 반음씩의 등분은 이에 대응하는 진동수의 비를 일정하게 정한다는 말과 같다.(식1)

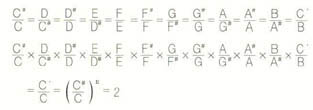
이에 따라 각 반음에 대응하는 진동수의 비를 ${}^{12}$$\sqrt{2}$≒1.0595 로 정해야 한다. (무리수가 이 곳에도 등장하는데, 이런 비는 수학자 메르센(Marin Mersenne, 1588-1648)이 처음으로 제시했다.) 그러므로 평균율에서 음정은 반음씩 증가하는 등차수열을 이루고, 이에 대응하는 진동수는 일정한 비율 ${}^{12}$$\sqrt{2}$로 증가해서 1옥타브 올라가면 2배가 되는 등비수열을 이룬다.

평균율은 복잡한 무리수의 비를 이용하지만 정수의 비를 이용하는 순정률에서 많이 벗어나지는 않는다. 예를 들면 5개의 반음으로 이루어지는 4도 음정과 7개의 반음으로 이루어지는 5도 음정에 대응하는 진동수의 비를 순정률과 평균율에서 비교해보면 다음과 같다.

음정 순정률 평균율
4도 $\frac{4}{3}$ ≒ 1.3333 ${({}^{12}\sqrt{2})}^{5}$ ≒ 1.3348
5도 $\frac{3}{2}$ = 1.5 ${({}^{12}\sqrt{2})}^{7}$ = 1.4983

평균율에서 유일한 순음정(pure inteval)은 1옥타브뿐이며 어울림 음정과 안어울림 음정이 건반 위에서는 동일한 음정으로 되는 모순이 있다. 그러나 평균율은 모든 장조와 단조가 연주 가능한 실용적 음계를 이루며, 자유로운 조바꿈과 조옮김은 물론 자유로운 화음 진행을 원활하게 한다는 장점이 있다.