각 문자를 고유한 숫자에 대응시키면 USA + USSR = PEACE가 된다.
풀어보고
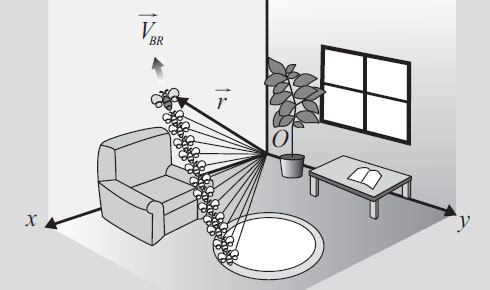
① 엉터리 수학자가 다음과 같은 계산을 했다. 이중에서 진짜로 틀린 식은?
② 1천개의 정육면체를 서로 붙여서 각 변의 길이가 10배인 커다란 정육면체를 만들었다. 이렇게 만들어진 큰 정육면체의 표면에 칠을 하고 다시 분리시켰을 때, 적어도 한면이 칠해진 정육면체의 개수는?
① 600 ② 520 ③ 488 ④ 480
③ 다음 문제에서 각 문자는 고유한 숫자를 의미한다. USA와 USSR은 초대강국인 미국과 소련을 뜻한다. 비록 USSR인 소련은 붕괴됐지만, 이 두나라가 오랜 기간의 냉전기를 갖지 않았다면 지구의 역사는 많이 바뀌었을 것이다. 따라서 다음과 같은 식이 성립될 수 있다.
USA
+USSR
PEACE
이 식에서 PEACE(평화)의 값은 얼마일까?
① 10270 ② 24564 ③ 15465 ④ 23793
④ 문자로 구성된 다음과 같은 식이 있다.
(YE)×(ME)=TTT
각 문자는 10이 넘지 않는 고유한 숫자를 갖는다고 할 때 E+M+T+Y는 얼마인가?
① 20 ② 21 ③ 22 ④ 23
⑤ 다음의 나눗셈을 완성하면 나눗수는 얼마인가?
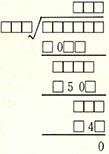
① 156 ② 215 ③ 316 ④ 459
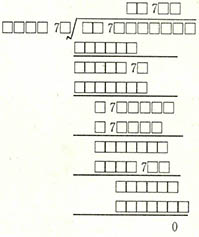
⑥ 다음의 제곱근을 구하는 공식을 완성하면 제곱근은 얼마인가?
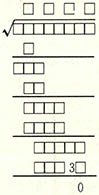
① 1562 ② 1986 ③ 2432 ④ 3194

맞춰보고
① ③세번째 식은 $\frac{8}{2}$-$\frac{9}{3}$=$\frac{8-9}{2-3}$가 되면 맞다. 이런 계산을 식으로 쓰면 $\frac{a}{b}$-$\frac{c}{d}$=$\frac{a-c}{b-d}$이 된다. 이 식을 전개시키면 ${a}^{2}$=-${b}^{2}$c+2bcd가 되고 양변을 c${d}^{2}$으로 나누면 $\frac{a}{c}$=$\frac{b}{d}$(2-$\frac{b}{d}$)가 된다.
이식의 의미와 a와 c를 계산하기 위해 b, d를 선택할 수 있다는 얘기다. 예를 들어 b=2, d=7이라면 $\frac{a}{c}$=$\frac{2}{7}$(2-$\frac{2}{7}$)=$\frac{2}{7}$×$\frac{12}{7}$=$\frac{24}{49}$이다. 그래서 a와 c는 각각 24, 49 또는 그의 배수가 된다. 따라서 다음 식이 성립한다.$\frac{24}{2}$-$\frac{49}{7}$=$\frac{24-49}{2-7}$또 문제에서처럼 b=2, d=3이라면 a=8, c=9가 된다.
한편 ④번과 같이 지울 수 있는 예도 여럿 있다. $\frac{19}{95}$=$\frac{1}{5}$, $\frac{16}{64}$=$\frac{1}{4}$, $\frac{49}{98}$=$\frac{4}{8}$
② ③이 문제를 어렵게 생각하면, 상당히 계산해야 할지 모른다. 발상의 전환을 하면 훨씬 쉬워질 수 있다. 칠해진 개수는 전체에서 안 칠해진 개수를 뺀 숫자다. 안 칠해진 개숫는 8×8×8개의 표면 내부의 정육면체가 된다. 즉 답은 ${10}^{3}$-${8}^{3}$=488이 된다.
③ ① 문제의 합을 보면 PEACE가 10,000보다 크고 11,000보다 작아야 됨을 금방 알 수 있다. 즉 P=1, E=0. 따라서 U=9가 된다. 그러면 맨 오른쪽부터 계산해 A+R=10, 1+S+S=C, 9+S=A+10(S=A+1)을 만족해야 함을 알 수 있다. C가 2S+1로 나타나므로 또 U가 9이므로 9보다도 작은 홀수가 된다. 또 C=2S+1=2A+3이고 P가 1이므로 A는 2보다 큰 수여서 C=2A+3≥2×2+3=7이 된다. 따라서 C=7이다. 최종 식은 다음과 같다.
932
+9338
10270
④ ② 정수인 TTT=T×(111)=T×3×37로 표시된다. 그러므로 ME와 YE는 37로 나눠질 수 있어야 한다. 또 문제의 식에서 T는 ${E}^{2}$의 끝자리 숫자와 같다. 따라서 ME를 택해보면 37이나 74가 돼야 한다. ME를 74로 놓으면 YE는 최소로 14가 되는데 ME×YE=74×14=1036>999. TTT는 최대 999이므로 ME는 74일수가 없다. 그러면 ME=37, T=9, 또 YE=$\frac{TTT}{ME}$=$\frac{999}{37}$=27이다. 따라서 E+M+T+Y=21이 된다.
⑤ ② 이 문제는 '숫자복원' 문제 중에서 쉬운 편에 속한다. 6자리의 숫자를 3자리의 숫자로 나눠 3자리의 결과를 얻는 것으로 힌두(즉 인도)에 기원을 두고 있는 문제다. 답은 다음과 같다.
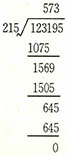
여러가지 문제중 조금 까다로운 것으로는 7만 남고 모두 지워진 다음과 같은 것이 있다.
여기서 나뉨수는 7375428413, 나눗수는 125473, 몫은 58781이다.
⑥ ④식의 셋째줄에서 넷째줄을 빼서 셋째줄의 맨 첫째 자리수가 없어지려면 셋째줄 첫번째 수는 1이어야 한다. 따라서 첫째줄과 둘째줄은 다음과 같이 돼야 한다.
3
$\sqrt{10}$
9
1
넷째줄을 만족하기 위해서는 제곱근의 둘째자리가 1이 돼야 한다. 따라서 근은 31□□가 되고 3100과 3199 사이의 수가 된다. 제곱수의 맨 끝부분이 3□로 끝났는데, 이 숫자는 36밖에 없다. 그런데 3100부터 3199까지의 수의 제곱수중 36으로 끝나는 숫자는 3194밖에 없다. 따라서 319${4}^{2}$=10201636이 원래의 문제다.