2022년 2월 러시아가 우크라이나를 침공하면서 두 국가 간의 전쟁이 발발했다. 2년 정도 이어진 전쟁으로 무고한 사람들이 희생됐다. 전쟁을 예측하고 준비한다면 이러한 피해를 줄일 수 있지 않을까.
실제로 전쟁과 테러 가능성을 예측하는 방정식을 고안한 사람이 있다. 2009년 뉴질랜드 물리학자 숀 고울리가 이끄는 연구팀은 뉴스에서 보도한 데이터를 수학적으로 분석해 무질서해 보이는 현대 전쟁에서 특징을 찾아냈다.
연구팀은 가장 먼저 뉴스와 비정부단체(NGO)가 작성한 만든 보고서에서 정보를 모아 전쟁과 테러에 대한 데이터베이스로 만들었다. 그리고 공격 시간, 공격 규모, 공격 장소, 무기의 종류 등을 변수로 다양한 그래프를 그렸다.
그 결과 x축을 공격으로 인한 사망자 수, y축을 (공격 횟수전체 공격 횟수)로 한 그래프에서 의미 있는 결과가 나왔다. 공격이 일어난 나라, 공격의 이유, 지지 세력 등이 모두 달랐지만, 기울기 α가 약 2.5인 직선이 나왔기 때문이다. 이라크와 아프가니스탄뿐만 아니라 세네갈, 페루, 인도네시아 등 10개국에서 일어난 전쟁과 테러에서도 똑같은 패턴이 나타났다.
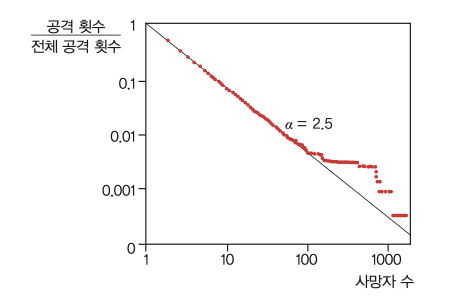
연구팀은 이를 바탕으로 공격 가능성을 예측할 수 있는 방정식을 만들었다.
공격 가능성을 알려 주는 수학 공식
P(x)는 어떤 나라에서 x명이 사망하는 공격이 발생할 가능성으로,
상수 C와 사망자 수의 -α제곱한 것과 같다.
여기서 α는 앞에서 설명한 직선의 그래프에서 기울기다.
α는 조직의 구조를 나타내는데, 조직이 응집하거나 흩어져 있는 정도를 알 수 있다. α값이 2.5로 유지되면 전쟁과 테러가 계속되고, α값이 커지면 공격 조직의 규모가 커지면서 한 조직이 여러 조직으로 나눠진다. 반대로 α값이 작아지면 조직의 규모는 작아지지만, 조직의 응집력이 강해 협상을 시도할 수 있다. 즉 이 방정식은 공격의 가능성을 예측해줄 뿐만 아니라 α값을 통해 어떤 전략을 써야 할지도 제시해준다.
연구팀은 이 방정식을 이용해 모의 실험을 했는데, 실제 전쟁을 비슷하게 재현할 수 있었다. 이 방정식으로 현대 전쟁의 패턴을 설명할 수 있으며, 전쟁의 양상을 어느 정도 예측할 수 있는 셈이다. 물론 모의 실험과 다르게 실제 전쟁에는 예상하지 못한 변수가 생길 수 있어 이를 완벽하게 입증하기는 어렵다. 하지만 수학을 이용해 전쟁을 예측할 수 있다면 그로 인한 큰 피해를 줄일 수 있다.
폭탄 테러를 막아라!
단시간에 엄청난 인명 피해를 내는 폭탄 테러가 일어날 날도 수학으로 예측할 수 있다. 2011년 영국 물리학자 닐 존슨은 연쇄 폭탄 테러 날짜를 예측하는 공식을 만들었다. 이 방정식은 두 번의 폭탄 테러가 똑같은 장소에서 일어난다고 가정했을 때, 두 공격 사이의 시간 간격을 방정식에 넣으면 다음 공격까지 시간이 얼마나 남았는지 알려 준다. 처음 일어나는 폭탄 테러를 예측하긴 어렵지만, 이후에 일어날 폭탄 테러 시기를 미리 알 수 있다.
다음 공격 날짜를 알려 주는 수학 공식
Γn = 다음 공격이 일어날 때까지 남은 시간
즉 n-1번 공격과 n번 공격 사이의 시간
Γ1 = 처음 공격과 두 번째 공격 사이의 시간
n = 공격 횟수(단, n=1, 2, 3, …).
-b = 폭탄 테러 학습 곡선을 따르는 상수
이게 가능한 이유는 폭탄 테러가 학습 곡선을 따르기 때문이다. 학습 곡선이란 시간이 지나면서 경험이 쌓여 일을 처리하는 시간은 줄어들고 정확성은 올라간다는 것을 그래프로 나타낸 것이다. 폭탄 테러의 경우 테러를 저지르는 횟수가 늘어날수록 성공할 확률이 지수함수 형태로 나타난다. 따라서 다음 공격까지 걸리는 시간은 지수함수를 따라 줄어든다.

란체스터 법칙으로 전쟁 승리 예측
전쟁의 승패는 ‘란체스터 법칙’이라는 수학 법칙으로 예측할 수 있다. 이는 영국 공학자인 프레데릭 란체스터가 제1차 세계대전 중이었던 1916년에 만든 법칙으로, 아군과 적군의 상대적인 힘을 계산하는 수학 이론이다. 그가 고안한 법칙 중 가장 유명한 법칙은 ‘란체스터 선형 법칙’과 ‘란체스터 제곱 법칙’이다.
란체스터 선형 법칙은 칼이나 창 같은 무기를 쓰는 근접전에 적용된다. 활이나 총 같은 원거리 무기는 사용하지 않는다고 가정한다. 이때 상대방의 전투력에 의한 손실은 미분 방정식으로 표현할 수 있다. 미분 방정식은 여러 가지 변수와 미분 식으로 이뤄진 수학 방정식으로, 순간 변화량을 측정하는 데 쓰인다.
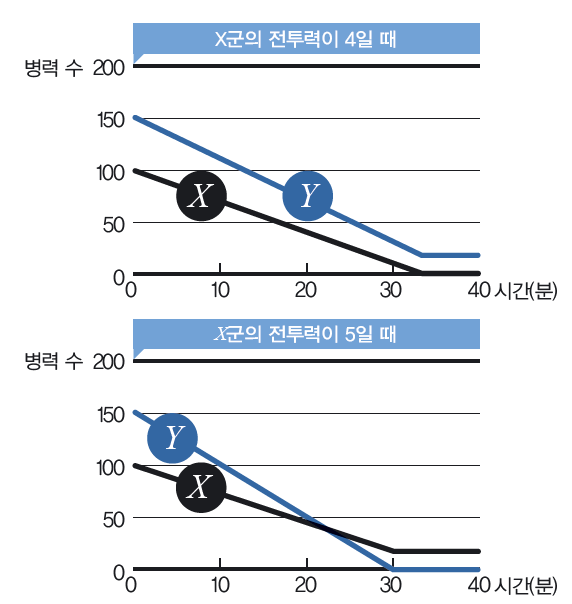
란체스터 선형 법칙으로 보는 전쟁 승패
전투력 1이 1분당 1명의 사상자를 낼 수 있는 수치라 생각하면 X군은 1분당 적 4명을, Y군은 적 3명을 때려눕힐 수 있다. 즉 1분이 지나면 X군은 97명, Y군은 146명이 된다. 2분이 지나면 각각 94명, 142명이 된다. 34분 뒤에는 X군이 모두 쓰러지고 Y군만 17명 남는다.
만약 X군의 힘이 5라면 어떨까. 계산해보면 30분 뒤 X군이 이긴다. 수적 열세를 극복하고 높은 전투력으로 승리한 것이다.
란체스터 제곱 법칙은 총과 같은 원거리 무기를 사용하는 전투에 적용되며, 원거리 전투에서는 근접전보다 병력이 더 중요해진다. 각 진영의 총 공격력은 병력의 제곱에 비례하기 때문이다.
란체스터 제곱 법칙에서는 두 미분 방정식을 이용해 병력 변화량을 계산한다. X군대와 Y군대가 전쟁을 치르고 있을 때, 한 군대의 전투력 손실은 다른 군대의 전투력 상승과 비례하고 다른 조건은 영향을 주지 않는다고 가정하자. 각 군대는 병력을 각각 x, y만큼 갖고 있다.
X군대의 전투력 손실량은 시간(t)에 따른 병력의 변화량이다. 미분법을 이용해 이 변화량을 수학식으로 나타내면 dx/dy 다. 공격 시 치명타를 준 비율을 ‘유효 사격률’이라고 할 때, Y군대 입장에서 X군대에게 치명타를 준 정도는 유효 사격률과 병력 수의 곱으로 나타낼 수 있다. 같은 방법으로 Y군대 기준으로도 식을 구할 수 있다. 따라서 다음과 같은 식이 나온다.

● Y군의 병력 변화량 = dt/dy = -a × y
a = X군의 유효 사격률 x = X군의 병력수
b = Y군의 유효 사격률 y = Y군의 병력수
X군과 Y군의 유효 사격률이 같은 경우(a = b) 전투 초반에 병사가 많은 쪽이 승리하고, 양측이 병력이 같은 경우(x = y) 화력이 큰 쪽이 승리한다. 또 x > y와 a > b일 경우 X군이 승리하고, x < y와 a < b일 경우 Y군이 승리한다.
한편 x > y와 a < b일 경우나 x < y와 a > b일 경우 b/a의 비율이 y/x의 비율 제곱보다 큰지 작은지에 따라 승리하는 쪽이 결정된다.
란체스터 법칙이 잘 맞아떨어진 사례도 있지만, 실제 전쟁에는 변수가 많아 이 법칙으로 설명되지 않는 경우가 대부분이다. 그렇다고 해서 란체스터 법칙이 아무짝에도 쓸모없는 건 아니다. 이런 이론은 더 나은 선택을 위해 참고 정도만 해도 충분히 가치가 있다. 현재 미국 육군에서는 란체스터 법칙을 변형해서 전투 시뮬레이션에 활용하고 있다.











