

과일가게 주인은 다 아는 수학 상식! 바로 케플러 추측입니다. 크기가 같은 공을 상자에 가장 많이 담으려면 피라미드 모양으로 쌓아야 한다는 것이지요. 그런데 이를 3차원이 아니라 더 큰 차원, 8차원과 24차원으로 확장하면 어떻게 될까요? 최근 우크라이나의 수학자가 이를 해결했습니다. 상상도 안 되는 8차원과 24차원에서는 케플러의 추측을 어떻게 풀어야 할까요?
커다란 상자 안에 크기가 같은 공을 가장 많이 넣고 싶습니다. 어떻게 하면 될까요? 시장이나 마트에서 사과나 오렌지를 상자에 담을 때 어떻게 담는지 보면 누구나 정답을 알고 있는 것 같습니다.
그런데 이 문제를 20년 전 수학자에게 물었다면 머리를 긁적이며 답을 하지 못했을 겁니다. 3차원 공간에서 같은 크기의 구를 최대한 많이 쌓는 방법은 오래된 미해결 문제였거든요. 1611년 독일의 수학자이자 천문학자인 요하네스 케플러는 피라미드 모양으로 쌓는 것이 최적이라고 주장했습니다. 즉 서로 맞닿도록 구를 촘촘하게 배열한 다음 그 위로구와 구 사이의 움푹 들어간 곳에 구를 쌓아 올려층을 만드는 겁니다. 이렇게 해야 3차원에서 공을 가장 많이 쌓을 수 있지요.

378년 난제, 컴퓨터로 증명
케플러의 추측이 옳다고 증명하는 일은 결코 만만치가 않았습니다. 무려 378년이나 미해결 난제로 남아 있었지요. 그러다 1998년 미국의 수학자 토마스 헤일스 피츠버그대 교수가 엄청난 양의 컴퓨터 계산을 통해 증명했습니다. 250쪽 분량의 논문은 3기가바이트 분량의 컴퓨터 프로그램 알고리즘과 계산 결과로 이뤄져 있었지요.
컴퓨터의 힘을 빌린 증명이라 헤일스 교수는 오류가 없는지 한 번 더 확인하고 싶었습니다. 그래서 2015년에는 연구진 21명과 함께 논문을 읽고 수학적으로 오류가 없는지 따지는 소프트웨어를 개발했습니다. 그 결과 증명이 틀리지 않았다는 걸 확인할 수 있었지요.
이제 케플러의 추측을 3차원이 아닌 n차원 문제로 확장해 봅시다. 한 점에서 거리가 1 이하인 점들의 모임을 반지름이 1인 구라고 합시다. 이때 각 차원에서 밀도는 얼마까지 높일 수 있을까요?
먼저 1차원을 생각해 봅시다. 1차원에서는 축이 하나밖에 없으므로 구는 길이가 2인 막대 형태로 나타납니다. 따라서 수직선 위에 길이가 같은 막대를 가장 많이 채우는 방법이 되지요. 하나의 빈틈도 없이 막대를 가득 채울 수 있기 때문에 밀도는 1입니다.


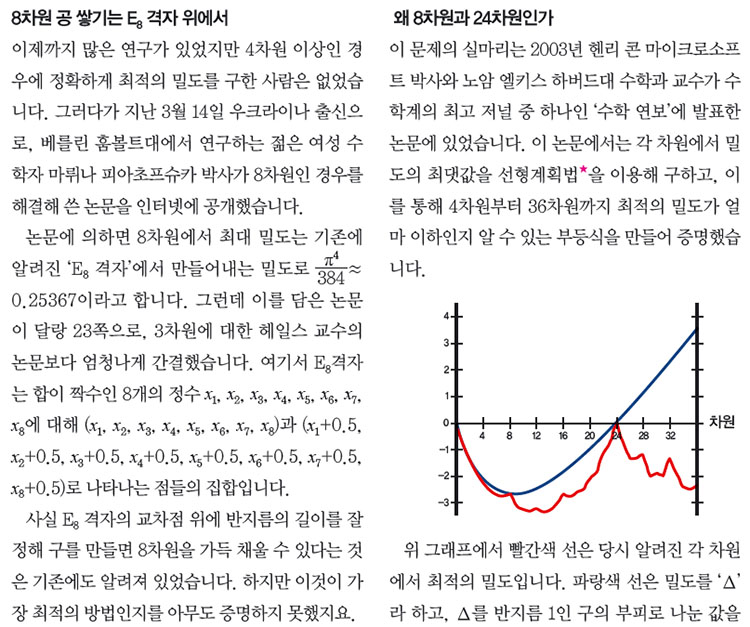



대부분 파랑색 선과 빨간색 선 사이의 간격이 큽니다. 하지만 8차원과 24차원에서는 두 그래프가 거의 만난 것처럼 보일 정도로 매우 가깝습니다. 실제로 2003년 논문에서 8차원일 때 최적의 밀도는 E8격자에서 구한 밀도의 1.000001배를 넘을 수 없다고 증명해 보였습니다. 이를 바탕으로 콘 박사와 엘키스 교수는 8차원과 24차원에서는 현재까지 알려진 가장 좋은 방법이 최적의 밀도일 거라고 추측했습니다.
피아초프슈카 박사는 8차원의 문제를 해결하기 위해 이 논문의 정리를 이용했습니다. 여기에는 특정 조건을 만족하는 함수를 잘 찾기만 하면 그걸 이용해서 최적의 밀도가 얼마 이하라는 점을 보일 수 있다고 설명한 정리가 있습니다. 문제는 이 함수를 찾기가 매우 어렵다는 겁니다.
그런데 피아초프슈카 박사가 정수론 분야에서 중요하게 사용하는 복소해석함수★인 ‘모듈러 형식’을 이용해 이 함수를 만들었습니다. 마치 모래사장에서 잃어버린 열쇠를 찾아 자물쇠를 여는 것처럼 딱 맞는 함수를 찾아낸 것이지요.
1주일 만에 풀린 24차원 문제
8차원 결과가 공개되자마자 콘 박사는 피아초프슈카 박사에게 24차원에 대해서도 할 수 있지 않냐고
이메일을 보냈습니다. 24차원에는 ‘리치 격자★’를 따라서 구를 채우면 밀도가 가장 높다는 추측이 있
었지요. 다행히 피아초프슈카 박사의 방법은 24차원에서도 통했습니다.
1주일 뒤 피아초프슈카 박사와 콘 박사, 인도 수학자 압히나브 쿠마, 미국 수학자 스티븐 밀러, 우크라이나 수학자 다뉠로 라드헹코 이렇게 5명이서 24차원 케플러 추측을 증명한 논문을 공개했습니다. 불과 1주일 만에 8차원을 풀었던 아이디어가 24차원으로 확장된 것이지요. 다음에는 어떤 차원의 문제가 해결될지 벌써부터 기대됩니다.












