d라이브러리

총상금 100억 원을 차지하기 위해 리얼리티쇼 ‘라이어 게임’에 참가한 사람들. 평소 생활고에 시달린 이들은 거액의 상금을 차지하기 위해 거짓말은 물론 배신도 서슴없이 한다. 과연 누구를 믿고 믿지 말아야 할까? 거액의 돈 앞에서 흔들리는 인간 심리를 수학으로 파헤쳐 본다.

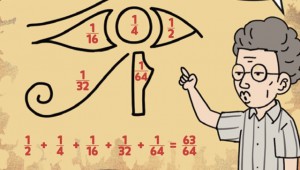
라이어게임의 필승법, 게임이론에 있다!

상대방을 속여야만 이기는 위험한 게임이 있다. 게임에서 이기면 거액의 상금을 거머쥐지만, 지면 엄청난 빚을 떠안을 수도 있는 ‘라이어게임’이다. 10월 말부터 방영 중인 드라마 <;라이어게임>;은 거짓말쟁이가 이기는 게임에 휘말린 여대생과 그를 돕는 천재 사기꾼의 이야기다. 일본 만화가 원작으로, 일본에서는 동명의 드라마와 영화가 큰 인기를 누렸다. 우리나라 드라마는 일본드라마를 우리 상황에 맞게 바꿨지만, 드라마를 이끌어 가는 게임은 원작과 같다.

게임의 큰 틀은 주최측이 각 참가자에게 나눠준 돈을 상대방을 속여서 가로채 오는 것이다. 물리적인 폭력만 쓰지 않는다면 어떤 방법을 사용해도 상관없다. 이렇게 뺏어온 돈은 고스란히 상금이 된다. 문제는 처음 받았던 돈을 주최측에 반납해야 한다는 것! 이 때문에 패자는 반드시 거액의 빚을 지게 된다. 승자에게 돈을 빼앗긴 마당에 처음에 받았던 돈도 반납해야 하기 때문이다.

우리나라 드라마에서는 라이어게임이 펼쳐지는 무대가 TV쇼로 바뀌면서 돈을 반납해야 하는 규칙은 없어졌다. 다만 중도 탈락하면 지금까지 받은 상금 전액을 반납해야 하는 규칙 때문에 참가자 중 많은 사람들이 빚을 떠안게 된다. 게임에 이기기 위해서는 지금까지 받은 상금을 쓸 수밖에 없는 상황이 벌어지기 때문이다.

그렇다면 빚을 지지 않고 모두가 이득을 얻는 방법은 없을까? 그 해답은 ‘게임이론’에서 찾을 수 있다. 게임이론이란 전략을 짜야 하는 상황에서 사람의 행동을 연구하는 수학의 한 분야다. 자신의 이익에 따라 협조했다가 때론 배신하는 사람의 이기적인 행동마저도 설명 가능하다. 이제부터 본격적으로 라이어게임을 수학의 눈으로 살펴보자.

모두가 상금을 타려면?

"아까 살려달라고 달려드는 사람들을 보고 생각했어요. 우리가 대체 왜 이래야만 하는 걸까? 누가 끝까지 살아남건 똑같이 상금을 나누기로 약속한다면 굳이 싸울 이유도 없고 빚질 일도 없고 다들 행복해지는 거 아니에요?"

라이어게임의 1라운드는 일대일 경기로 펼쳐지는 ‘5억 게임’이다. 규칙은 간단하다. 방송국에서는 참가자 전원에게 5억 원씩 지급한다. 이 돈을 일주일 동안 잘 보관했다가 반납하면 된다. 그 동안 폭력을 뺀 어떤 방법으로든 다른 사람에게서 5억 원을 빼앗으면 그 돈은 상금이 된다. 5억 게임의 참가자들은 상대방과 협력하느냐 배신하느냐에 따라 다음과 같은 상황에 처할 수 있다.

➊ 서로 협력해 둘 중 한 사람을 승자로 만들고 5억 원의 상금을 반씩 나눠 갖는다.
➋ 둘 중 하나가 배신해 돈을 빼앗으면 배신자만 상금 5억 원을 갖는다.
➌ 둘 다 배신해 승패를 가리지 못하면 상금은 없다.
 
이 상황 중에서 어떤 선택을 해야 나에게 가장 이득이 될까? 만약 참가자 A와 B가 서로 협력하기로 약속했다고 하자. 그런데 평소 자기밖에 모르는 B가 A를 배신한다. 하지만 중간 결과 발표로 이는 들통나고 만다. 화가 난 A가 덩달아 B를 배신한다. 그런데 이렇게 되면 둘 다 한 푼도 벌지 못한다. 따라서 둘은 다시 서로 협력하게 된다. 이것이 바로 ‘내시 균형’이다.

내시 균형은 1994년 노벨 경제학상을 받은 미국의 수학자 존 내시가 고안한 것으로, 게임에서 경쟁자의 행동에 따라 최선의 선택을 하면서 서로 자신의 선택을 바꾸지 않는 균형 상태를 말한다. 즉, 수학적으로 따졌을 때 참가자들은 서로 협력해서 상금을 나눠 갖는 것이 가장 최선이다.

드라마에서는 2라운드 소수결 게임에서 하우진과 남다정 등 8명이 동맹을 맺고 이 중 한 사람이라도 우승자가 나오면 상금을 나눠 갖기로 한다. 이것이 바로 내시 균형이다.

배신이 만연한 게임에서 이기려면?

"자업자득이야. 사실 처음 네가 한 제안, 서로 믿고 누가 떨어지더라도 상금을 나누자는 것이 가장 안전한 방법이었어. 하지만 저들은 내심 상금을 나누지 않고도 나 대신 아무나 떨어지기를 바랐던 거야. 나만 아니면 된다는 그 이기심이 화를 부른 거지."

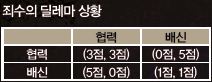
사실 여자 주인공 남다정(김소은 분)은 줄곧 서로 협력하자고 제안한다. 하지만 그녀의 말에 귀 기울이는 이는 없다. 몇몇은 사리사욕에 눈이 멀어 협력하기로 해놓고도 배신을 일삼는다. 이런 상황을 게임이론의 관점으로 살펴보면 ‘죄수의 딜레마’라고 할 수 있다. 협력할 경우 서로에게 가장 이익이 되는데, 개인적인 욕심으로 서로에게 불리한 상황을 만드는 것이다. 5억 게임의 경우에는 서로 협력하면 2억 5천만 원씩 나눠 가질 수 있는데, 한 명이 배신하면 다른 사람은 상금을 얻지 못하게 된다.

그런데 라이어게임의 2라운드부터는 1대1 대결이 아닐 뿐더러 죄수의 딜레마 상황이 반복해서 일어난다. ‘소수결’과 ‘정리해고’ 게임에서는 규칙이 같은 게임을 여러 차례 반복하기 때문이다. 그렇다면 이럴 때는 어떻게 대응해야 할까? 만약 배신한 동료가 있다면 이를 그대로 지켜봐야만 하는 걸까?

이 문제를 간단하게 해결하는 전략이 있다. 바로 ‘팃포탯’이다. 일명 눈에는 눈, 이에는 이 전략이다. 배신을 당하면 어김없이 복수하는데 단 한번으로 경각심을 일으키는 전략이다. 이 방법은 1981년 미국의 수리심리학자 아나톨 래퍼포트가 고안했다. 그는 미국의 정치학자 로버트 액설로드가 개최한 ‘반복적 죄수의 딜레마 게임 컴퓨터대회’에 참가했는데, 이때 팃포탯 전략으로 2회 연속 우승을 차지했다.

팃포탯에는 중요한 원칙 4가지가 있다. 바로 다음과 같다.

➊ 대결 상대가 배신하기 전까지는 항상 협력한다.
➋ 대결 상대가 배신하면 반드시 복수한다.
➌ 복수한 뒤에는 빠르게 관용을 베푼다.
➍ 한번 대결을 펼친 상대와 또 대결을 해도 사이가 좋도록 좋은 관계를 유지한다.

이 원칙 아래 경기를 진행해 간다. 그런데 만약 참가자가 다음 게임이 마지막이라는 것을 알면 자연히 더 많은 상금을 얻기 위해 배신할 가능성이 높다. 따라서 상대방이 이게 몇 번째 죄수의 딜레마 상황인지 모르게 진행해야 게임을 더 유리하게 할 수 있다.

팃포탯 맛보기

"저는 라이어게임에 참여하는 내내 계속 생각해 봤어요. 정말 속고 속이기 위해 만들어진 쇼인 걸까? 그럴 수도 있죠. 하지만 달리 생각해 보면 우리가 정말 서로를 믿을 수 있는지 시험하는 걸 수도 있다는 생각이 들어요. 전 여러분을 믿고 싶어요."

이제 실제 게임에서 팃포탯 전략이 어떻게 적용되는지 보자. 여기 4명의 게임 참가자가 있다. A와 B는 팃포탯 전략을 사용하고, C와 D는 자신만 이익을 얻기 위해 배신을 한다. 참가자는 다른 3명과 각각 6번씩 총 18번의 게임을 한다. 이때 협력하면 둘 다 3점을 얻을 수 있다. 배신하면 배신한 쪽이 5점을 얻지만, 협력한 사람은 점수를 얻지 못한다. 둘 다 배신할 경우 모두 1점을 얻는다.
 
먼저 팃포탯 전략을 사용하는 A와 배신자 C의 게임을 살펴보자. 첫 번째 게임에서 A와 C는 협력하기로 했지만 C는 곧바로 배신한다. 따라서 A는 0점, C는 5점을 얻는다. 이제 둘의 신뢰 관계는 깨졌기 때문에 나머지 5경기 모두 서로 배신하게 된다. 따라서 A의 총합은 5점이고, C의 총합은 10점이다.

다음 게임은 둘 다 팃포탯 전략을 쓰는 A와 B의 경기다. 둘은 6번 모두 협력을 하기 때문에 둘 다 18점씩 얻는다. C와 D, 배신자끼리 게임을 하면 6경기 모두 배신하기 때문에 C와 D가 얻는 점수는 6점씩이다.

이를 토대로 총 18번의 게임에서 얻은 총점을 계산해 보면 팃포탯 전략을 사용한 A와 B는 각각 다른 참가자와의 게임에서 28점(=5+5+18), 배신자 C와 D는 각각 26점(=10+10+6)을 얻게 된다. A와 B는 단 한 게임에서도 5점을 획득한 적이 없고, C와 D는 0점을 얻은 적이 없지만, 놀랍게도 팃포탯 전략을 쓴 참가자의 최종 점수가 더 높다. 실제로 팃포탯 전략을 쓰는 참가자가 많을수록 더 많은 이득을 챙길 수 있다. 만약 이 전략을 쓰는 참가자가 적다면 이득이 줄어들지만, 그래도 배신자보다는 더 많은 이득을 얻게 된다.

17포커의 필승법은 합동!

이번에는 원작 만화에 나온 17포커의 필승법을 살펴보자. 17포커란 가장 대표적인 카드 게임, 포커와 규칙이 같다. 단지 각각 4장씩인 에이스와 잭, 킹과 퀸, 그리고 한 장의 조커 이렇게 총 17장의 카드만 사용한다. 참가자는 딜러에게서 5장의 카드를 받는다. 한 번의 카드 교환 기회를 이용해 2장 이상 같은 문자가 나열되도록 카드를 만들어야 한다. 같은 문자가 많이 나온 사람이 이기기 때문이다. 게임은 총 10번 진행되는데, 매번 새 트럼프를 사용하고 힌두 셔플★과 리플 셔플★만을 사용해서 카드를 섞는다.

남자 주인공 아키야마 신이치는 이미 승패가 기운 분위기에서 힌두 셔플로 섞으면 카드 뒷면에 뭐가 있는지 훔쳐 볼 수 있으니 리플 셔플로만 섞고, 참가자가 주문한대로 여러 번 섞자고 제안한다. 상대방은 흔쾌히 이를 받아들이고 게임이 다시 시작되는데, 이때부터 신이치가 줄곧 이긴다. 대체 어떻게 된 걸까?

바로 리플 셔플에 숨겨진 ‘합동★’의 개념 때문이다. 합동이란 정수론에 등장하는 용어로, 정수 a와 b의 차가 정수 m으로 나눠떨어질 때 쓰는 표현이다. a와 b를 두고 mod m에서 합동이라고 한다. 합동이면 a와 b를 각각 m으로 나눈 나머지도 같다.

그렇다면 대체 리플 셔플과 합동이 무슨 관계일까? 카드 17장으로 리플 셔플을 계속해서 해 보자. 2번 또는 6번 섞으면 같은 문자 4개가 연달아서 배열된다. 8번 섞으면 카드 배열이 맨 처음과 같아진다. 즉 8로 나눴을 때 나머지가 2이거나 6인 횟수로 리플 셔플을 요구한 뒤 카드를 여러 장 바꾸면 그만큼 같은 문자 카드를 얻을 수 있다.

이처럼 최고의 거짓말쟁이를 가리는 대회인줄만 알았던 라이어게 임의 필승법은 수학에서 찾을 수가 있었다. 드라마와 만화를 보면서 기사에 소개되지 않은 수학 필승법을 찾아보는 건 어떨까?
 
힌두 셔플★ 카드 무더기에서 일부를 떼어낸 다음 맨 위에 있는 카드부터 순차적으로 다른 한쪽에 내려놓아 카드의 순서를 역순으로 만드는 방법.
리플 셔플★ 반으로 나눈 카드를 좌르륵 소리를 내며 양손에서 번갈아가며 한 장씩 떨어지도록 하는 기술.
합동★ 14와 20은 mod 6에서 합동이다. 14와 20의 차인 6이 6으로 나눠떨어지기 때문이다.