d라이브러리

생일 축하합니다~. 생일 축하합니다~. 사랑하는 수학동아, 생일 축하합니다! 수학동아가 열두 번째 생일을 맞았어요. 이번에는 생일하면 빠질 수 없는 케이크를 만들어 보겠습니다. 또 케이크를 공평하게 나눠 먹으려면 어떻게 자르는 것이 좋을지 같이 알아 볼까요?

※ 편집자 주

LOL, 오버워치, 배그부터 다양한 인디게임까지 섭렵한 게임 인생 6년 차 퓨처킴. 하지만 마인크래프트는 처음이다. 회사에서 게임을 하는 것이 조금은 눈치 보이지만 마크의 초고수가 되는 그날까지, 나는 달린다!

만약 먹을 수 있는 진짜 케이크를 만들었다면 수학동아 편집팀이 즐겁게 나눠 먹었을 거예요. 그런데 여럿이 음식을 먹을 때마다 고민되는 게 있습니다. 바로 ‘어떻게 공평하게 나눌까?’입니다. 모든 사람이 공평하게 케이크를 나눠 먹기 위해선 어떻게 케이크를 잘라야 할지 알아볼까요?

공평하게 케이크 나누기

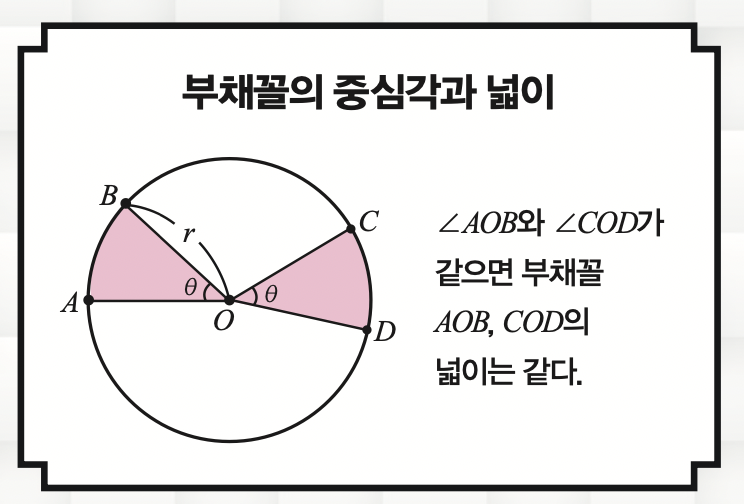
우선 높이를 고려하지 않고 평면에 놓인 원 모양의 케이크를 편집팀 6명이 나눠 먹는다고 해볼게요. 이때 원의 성질을 알고 있다면 케이크를 공평하게 자를 수 있습니다. 위의 그림처럼 원의 중심 O와 원 위의 두 점 A, B가 이루는 도형을 부채꼴이라고 하고 부채꼴 AOB라 부릅니다. 이때 선분 OB와 선분 OA가 이루는 각을 중심각이라고 하고 ∠AOB로 나타내죠. 원의 성질 중 중심각의 크기가 같은 부채꼴은 넓이가 같다는 성질이 있습니다. 이 성질에 따라 공평하게 케이크를 나누기 위해선 중심각이 같도록 원을 나누면 됩니다. 그럼 원 전체의 중심각인 360 ° 를 6으로 나눠 중심각이 60 ° 이고 넓이가 같은 부채꼴 6개로 나눌 수 있습니다.

이제 실제 원기둥 모양의 케이크를 생각해볼게요. 원기둥의 부피는 원의 넓이에 높이를 곱해 구할 수 있습니다. 원기둥뿐만 아니라 위아래의 단면이 같은 기둥꼴 도형 역시 밑면의 넓이에 높이를 곱해 부피를 구할 수 있어요. 케이크의 높이는 일정하므로, 부채꼴의 넓이가 모두 같다면 부채꼴 기둥의 부피도 모두 같습니다. 결국 원기둥 모양의 케이크를 공평하게 나눌 땐 같은 중심각을 가진 부채꼴 기둥으로 나눠야 하죠.

모두가 만족하는 케이크 나누기

나누어 먹을 케이크가 여러 맛이 섞여 있는 아이스크림 케이크라고 생각해봅시다. 사람마다 취향이 달라서 똑같은 크기로 잘랐다고 해도 불만이 생길 수 있어요. 이렇게 서로 원하는 부분이 다를 경우에 모두가 만족하도록 나누는 법은 무엇일까요?

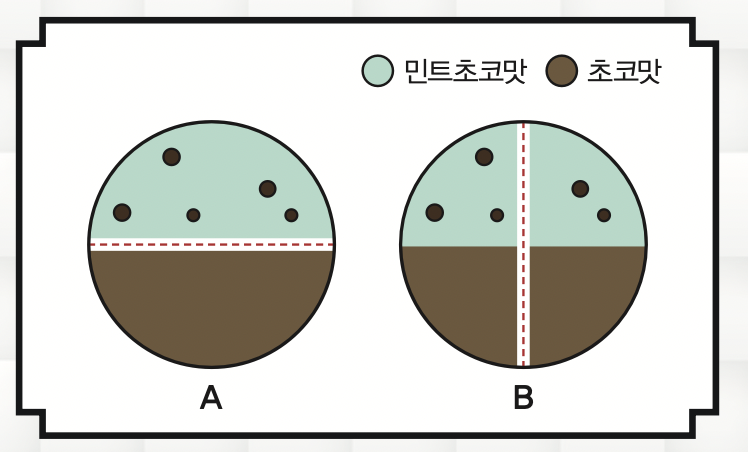
우선 두 사람만 케이크를 먹는다면,  이 문제는 간단하게 해결됩니다. 둘 중 한 명이 케이크를 반으로 나누고, 다른 한 명이 가져갈 케이크를 먼저 고르는 거예요. 만약 태인이 민트초코맛을 몽땅 먹고 싶어서 A처럼 잘랐다고 가정해볼까요? 선택권은 아름에게 먼저 있어서 아름이 민트초코맛 부분을 다 가져갈 수도 있습니다. 그럼 태인은 민트초코맛을 입에 댈 수도 없죠. 결국 태인은 전략적으로 민트초코맛을 B처럼 반으로 나누는 선택을 할 겁니다. 그럼 사람이 늘어난다면 어떻게 나눠야 할까요?

1960년대의 비슷한 시기에 미국 수학자 존 셀프리지와 영국 수학자 존 호턴 콘웨이는 3명이 만족하도록 케이크 나누는 방법을 떠올리고, 그 방법을 이용하면 모두 만족할 수 있다는 것을 수학으로 증명했습니다. 이 방법에 따르면 최대 5번 자를 때 공평하게 나눌 수 있죠. 이후 많은 수학자가 더 많은 사람이 있을 때 공평하게 케이크를 나누는 알고리듬을 만들어 컴퓨터로 이 문제를 풀려고 시도했습니다. 하지만 약 55년 동안 이렇다 할 최적의 알고리듬을 찾지 못했어요.

그러던 중 2016년 4월 호주의 수학자 하리스 아지즈와 사이먼 멕켄지가 새로운 케이크 분배 방법을 논문 사전 공개 사이트인 ‘아카이브’를 통해 제안했습니다. 그 방법에 따르면 4명일 때 최대 203번 칼질로 공평히 자를 수 있고, n명일 때 공평하게 케이크를 나눠 먹기 위해선 n^{_n^n^n^n^n}번 이내로 칼질해야 한답니다. 이 연구는 획기적인 공평한 케이크 나누기 방법을 제시했다는 평가를 받으며 2016년 열린 IEEE(Institute of Electrical and Electronics Engineers) 컴퓨터 과학 기초 심포지엄에서 소개됐습니다.    

수학자들은 케이크조차 평범하게 먹지 않네요. 혹시 여러분만의 공평한 케이크 나누는 법이 있나요? 없다면 이번 기회에 새로운 방법을 찾아보는 건 어떨까요?