뜨개질 하는 수학자들
뜨개질을 한다고 하면, 누군가에게 선물할 목도리를 짜는 여자 친구나 흔들의자에 기대 앉아 실을 꿰는 할머니를 떠올릴지 모른다. 그런데 여기 뜨개질을 하는 수학자들이 있다. 이들은 수학 뜨개질을 주제로 미국수학학회 특별 컨퍼런스에 모여 각자가 만든 작품을 발표하고 전시회를 열었다. 2014년이 세 번째 컨퍼런스였다. 수학 개념을 담은 뜨개 옷과 뫼비우스 띠 모양의 목도리, 혹은 머리 끈처럼 실제로 쓸 수 있는 물건을 만들기도 한다.
왜 수학자들이 뜨개질을 하는 걸까? 특별 컨퍼런스를 기획한 수학자 사라 마리 벨캐스트로 박사에 따르면, 수학 뜨개질은 크게 두 가지 의미로 해석할 수 있다. 하나는 수학을 이용해 뜨개질을 하는 것이고, 다른 하나는 뜨개질을 수학적으로 연구하거나 뜨개질을 활용해 수학을 연구하는 것이다.
수학적 개념을 나타내는 모양을 만들면, 수학 이론을 연구하거나 학생들을 가르치는 데 도움이 된다. 뜨개질 모형은 3차원 구조를 자세히 뜯어볼 수 있고, 유연한 실물을 손으로 만져 볼 수 있기 때문에 정교한 컴퓨터 모델보다 유용할 수 있다.
뜨개질로 수학 작품을 만드는 것 자체가 수학 연구에 도움이 되기도 한다. 130년 전 스코틀랜드의 화학자 알렉산더 크럼 브라운은 화학 분자의 3차원 구조에서 아이디어를 얻어, 복잡한 함수를 뜨개질 모델로 만들었다. 이 모델은 이후 ‘분자의 화학적 성질은 원자들이 어떻게 꼬여서 매듭을 이루고 있는가에 달려 있다’는 켈빈의 ‘볼텍스 이론’과 함께 ‘매듭이론’이라는 수학 이론의 토대가 됐다.
아무리 복잡한 3차원 형태도 함수를 이용해 모델로 만들면, 쉽게 뜨개질할 수 있다. 수학 개념을 활용하면 기하학적 패턴도 무궁무진하게 디자인할 수 있다. 수학 알고리듬이나 수학 퍼즐에 담긴 규칙을 따라 여러 경우의 수를 만들어낼 수 있기 때문이다. 또한 수학적인 분석을 통해 좀 더 효율적인 뜨개질을 할 수도 있다.


인터뷰

“뜨개질을 하면 수학이 보여요.”
사라 마리 벨캐스트로
수학 뜨개질과 관련된 활동을 주도해온 사라 마리 벨캐스트로 박사는 얼마 전까지 미국 사라로렌스대 수학과 교수로 지냈고, 현재는 미국 스미스칼리지 수학과 연구원으로 재직 중이다. 고등학생을 대상으로 하는 수학 캠프를 주관하는 비영리단체 ‘MathIY’의 총감독을 맡고 있기도 하다. 그녀와 수학 뜨개질에 관해 이야기를 나눴다.
Q 수학 뜨개질을 시작하게 된 계기는 무엇인가요?
A 어려서부터 수학을 좋아했고, 뜨개질은 초등학교 때부터 할 줄 알았어요. 그래서 정확히 언제부터 수학 뜨개질을 시작했는지는 잘 기억이 나지 않지만, 아마 고등학교 1학년 때일 겁니다. 당시에 저는 정말 뜨개질을 많이 했어요. 위상수학 시간에 안쪽 면과 바깥쪽 면이 구분되지 않는 클라인 병을 배운 뒤, 4차원 물체를 손으로 직접 느껴보고 싶다는 생각을 했죠. 완벽하지는 않았지만 스스로 만들었다는 데 신이 나서 교수님께 보여 드렸어요. 그 뒤로 어떻게 하면 수학적인 개념을 뜨개질로 표현할 수 있을지 고민했습니다.
Q 미국수학학회에서 수학 뜨개질을 주제로 특별 컨퍼런스를 기획한 이유는 무엇인가요?
A 수학 뜨개질 특별 컨퍼런스는 미국 머서대 수학과 캐롤린 야켈 교수와 제가 공동 주최했어요. 사실 수학자들도 수학 뜨개질에 대해 잘 모르는 경우가 많았거든요. 뜨개질의 유용성을 더 많은 수학자들과 공유하고 싶었어요. 그리고 특별 컨퍼런스에 참여한 수학자들이 발표한 이야기를 책으로 엮어, 누구나 볼 수 있게 만들었죠.
Q 뜨개질이 수학 연구에 어떤 도움이 되나요?
A 실로 짠 뜨개질 작품은 선과 면의 관계를 잘 드러내 줘요. 뜨개질을 통해, 복잡한 곡면 위에 직선과 곡선이 어떻게 놓이는지 쉽게 알 수 있죠. 이런 점이 수학 연구에 많은 도움이 됩니다. 뜨개질 안에 담긴 매듭과 그 매듭이 물체가 되어가는 과정 자체를 연구하는 것도 수학의 연구 분야가 됩니다. 뜨개질 자체가 연구 주제가 되는 거죠.
Q 수학 뜨개질을 하려는 독자들에게 한마디 해 주세요.
A 뜨개질은 일종의 수학 실험이라고 생각할 수 있어요. 추상적인 개념을 눈으로 볼 수 있는 것으로 만들려면, 나타내고자 하는 추상적 개념의 핵심을 잘 파악하는 게 중요합니다. 뜨개질을 하면서 수학을 깊이 있게 탐구하려고 노력해 보세요. 그 전에는 몰랐던 새로운 것들이 눈에 보일 거예요. 뜨개질 과정 자체에 대한 기하학적인 이해도 필요합니다.
뜨개질 도와 주는 수학
수학을 활용하면 뜨개질을 할 때 어떤 점이 좋을까. 뜨개질 패턴을 만들어 주는 알고리즘부터 최적의 뜨개바늘 경로를 찾는 방법까지…. 수학적 원리와 모델을 활용하면 뜨개질을 쉽고 재밌게 할 수 있다.
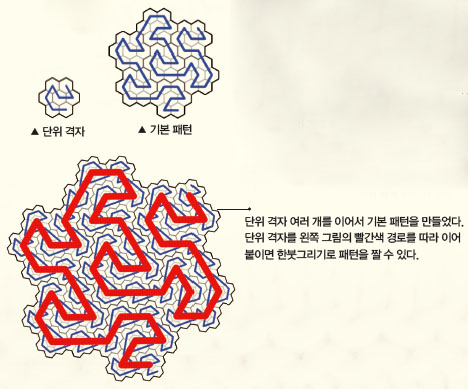
힐베르트 곡선으로 한붓그리기
뜨개질은 두꺼운 실을 촘촘히 짜서 면이 되도록 하는 것이다. 즉, 빈 공간에 선을 그려 평면을 만드는 것이다. 하지만 무작정 백지에 패턴을 그리려고 하면 막막하다. 그렇다면 몇 가지 수학적 규칙을 따라 선을 그려보는 것은 어떨까.
‘힐베르트 곡선’으로 평면을 채우면 여러 가지 패턴을 만들 수 있다. 평면을 격자로 나타내고 모든 칸의 중심을 한 번씩 지나도록 끊어짐 없이 선을 그리면, 패턴을 만들 수 있다.
정육각형 격자 위에 힐베르트 곡선을 그리는 방식을 적용하면, 다양한 패턴을 만들 수 있다. 선이 끊어지지 않게 한붓그리기로 실을 짜려면, 기본 패턴의 시작점부터 끝점까지의 경로와 단위 격자를 이어 붙인 경로가 닮은 꼴이 돼야 한다.

수학적으로 가장 효율적인 뜨개질
수학자들은 최적의 뜨개질 방법을 찾기도 한다. 보통 티셔츠 하나를 개려면 4번을 접어야 하지만 처음에 잡는 위치를 잘 선택해 개면 단 2번 만에 티셔츠를 접을 수 있다. 뜨개질도 마찬가지다. 어떻게 실을 엮느냐에 따라 같은 모양을 만들 때 필요한 뜨개질 횟수가 달라질 수 있다. 똑같은 물체를 만들더라도 최소한의 바늘 수로 뜨개질 할 수 있다면, 훨씬 시간과 수고를 덜 수 있다. 가능한 짧은 길이의 실로 뜨개질 하는 방법도 있다.
복잡한 뜨개질은 뜨개바늘 지도로
간단한 물체가 아닌 복잡한 물체, 혹은 엄청나게 큰 물체를 짤 때는 어떤 지점에서 뜨개질을 시작할지 결정하는 게 중요하다. 무작정 뜨개질을 시작했다가 원하는 물체가 만들어지지 않을 수도 있다.
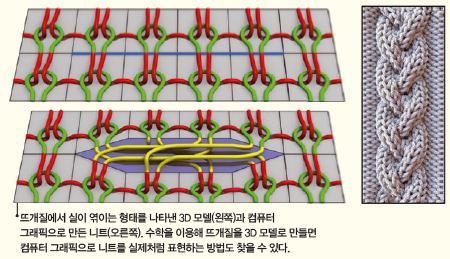
뜨개질을 함수로 나타내 3D 컴퓨터 모델로 만들면, 어떤 경로로 바늘이 움직여야 뜨개질이 되는지 눈으로 확인해 볼 수 있다. 일종의 바늘 지도다. 이 모델을 보면서 뜨개질을 하면, 초보자도 어렵지 않게 복잡한 입체 구조를 뜨개질 할 수 있다.
정사각형 여러 개로 직사각형 만들기
크기가 다른 정사각형 여러 개로 하나의 직사각형을 만드는 방법으로 패턴을 디자인할 수도 있다. 실의 색깔을 바꿔가며 뜨개질을 하고, 이렇게 만든 정사각형을 서로 이어서 직사각형을 만드는 것이다.
이때 몇 가지 규칙을 따르면, 문제가 좀 더 간단해진다. 아래 규칙을 따라 패턴을 만들어 보자. 각 정사각형의 색깔과 크기, 개수에 따라 만들어질 수 있는 패턴의 경우의 수가 많이 생긴다. 따라서 같은 규칙이라 해도 서로 다른 패턴이 나올 수 있다.
● 정사각형만을 사용해 직사각형을 만든다.
● 정사각형 한 변의 길이는 정수이고, 모든 정사각형의 크기는 서로 다르다.
● 직사각형을 이루는 각각의 정사각형을 서로 구분할 수 있도록 이웃한 정사각형끼리는 서로 다른 색깔을 쓴다.
● 사용하는 색깔의 수는 최소가 되도록 한다.
수학 도와 주는 뜨개질
실제로 뜨개질은 교육과 연구를 위해 많이 쓰이고 있다. 뜨개질 모델을 직접 만들어 보면서, 우리는 실이 어떤 경로로 진행하고 서로 교차하는지 알 수 있다. 실의 색깔을 서로 구분해서 짜면, 곡선이 곡면을 어떻게 구성하는지 눈으로 관찰할 수 있기 때문이다. 그래서 뫼비우스 띠나 클라인 병, 쌍곡면 등 보통의 평면에서는 이해하기 어려운 입체 구조를 이해하는 데 유용하게 쓰인다. 이론만으로는 이해할 수 없는 부분이나 이론과는 다른 부분에 대해 새롭게 알게 되기도 한다.
쌍곡 기하학 평면 위의 이상적인 삼각형
보통 우리가 평면이라고 알고 있는 것은 유클리드 기하학에서 말하는 평면이다. 이런 평면 위에서 삼각형 내각의 합은 180°다. 그러나 쌍곡 기하학 평면 위에서는 삼각형 내각의 합이 180°보다 작다. 오른쪽 그림은 수학자 푸앵카레가 쌍곡 기하학 평면과 그 위에 그려진 이상적인 삼각형을 간단히 나타낸 모델이다.
쌍곡 기하학 평면 위의 이상적인 삼각형은 원의 일부인 부채꼴의 호를 세 변으로 한다. 이런 이상적인 삼각형의 가장 대표적인 특징은 ‘같은 쌍곡 기하학 평면 위에서는 서로 다른 모든 삼각형의 넓이가 항상 같다’는 것이다. 언뜻 보기엔 전부 다를 것 같지만, 실제로는 모두 같다.
이렇게 쌍곡 기하학 평면 위에서 나타나는 도형의 특이한 성질을 가장 쉽게 탐구해 볼 수 있는 도구가 뜨개질 모형이다. 뜨개질로 만든 쌍곡 기하학 평면 위에 구분할 수 있는 다른 색깔의 실로 삼각형을 표시하고, 이 모형을 이리저리 구부리고 접어 보면서 삼각형의 특성을 관찰할 수 있기 때문이다.

뜨개질로 직접 보는 위상동형
뜨개질을 활용하면 어려운 도형 개념을 실험을 통해 쉽게 이해할 수 있다. 도형에서 합동이라 하면 형태를 변형시키지 않고 단지 평행이동이나 대칭이동, 회전이동을 했을 때 겹쳐지는 두 도형을 의미한다. 하지만 공간 속의 점과 선, 면의 위치 관계와 형상을 연구하는 위상수학에서는 구부리고 늘이고 줄이는 것 같은 변형을 거쳐 서로 같은 형태로 만들 수 있는 두 도형을 같은 도형으로 생각한다. 이런 도형을 ‘위상동형’이라 한다.
오른쪽 사진은 뜨개질로 만든 쌍곡면 치마와 클라인 병이다. 색깔 별 실의 양이나 놓이는 위치를 동일하게 유지한 채로 꿰었던 실을 풀어 모양을 바꾸고 이를 다시 연결해 만들었다. 이들은 서로 위상동형이다.

뜨개질로 찾은 토러스 매듭 알고리즘
뜨개질과 가장 직접적인 연관을 갖는 연구 분야가 바로 매듭이론이다. 매듭이론은 양 끝이 이어진 수학 매듭을 교차점 수와 같은 기준으로 종류별로 분류하고, 이들의 특성을 연구하는 학문 분야다. 보통 매듭은 긴 줄을 꼬아 묶은 것이지만, 수학에서의 매듭은 이 줄의 양 끝을 이어 붙인 닫힌 곡선을 의미한다.
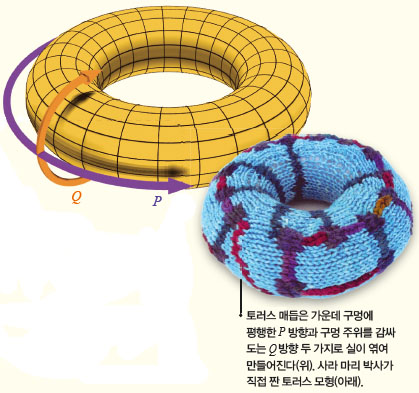
위상수학을 연구하는 사라 마리 박사는 직접 뜨개질을 직접 하며 토러스 매듭 알고리즘을 고안했다. 토러스 매듭은 도넛 모양을 이루며 매듭이 연결돼 있는 것이다. 가운데 구멍에 평행한 P와 구멍 주위를 감싸 도는 Q의 두 가지 방향으로 엮인 실로 이뤄져 있다.
이 두 고리가 각각 한 바퀴를 도는 횟수가 p, q이면 이를 ‘(p, q) 토러스 매듭’이라고 한다. 사라 마리 박사는 이 정수 사이의 규칙을 찾아 무한히 많은 종류의 토러스 매듭을 만드는 알고리즘을 만들었다.
털뭉치로 분류한 대칭 패턴
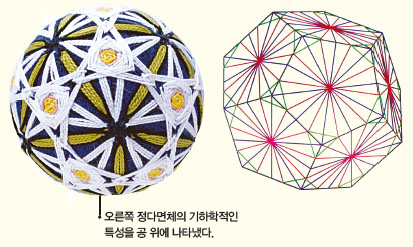
특별 컨퍼런스의 공동 주최자인 캐롤린 야켈 교수는 사라 마리 박사와 함께 구로 나타낼 수 있는 대칭의 종류를 밝혔다. 유클리드 기하학에서 모든 정다면체는 구에 내접할 수 있다.
캐롤린 교수는 이를 활용해 구 안에 정다면체가 내접했다고 가정하고 구 표면에 정다면체의 핵심 요소를 표시했다. 예를 들어 꼭짓점에는 별을 표시하고 그 별을 직선으로 이어 구획을 나눴다. 이렇게 구형의 털뭉치 위에 여러 가지 정다면체의 기하학적 특성을 나타내고, 대칭의 종류를 분류했다.