d라이브러리

종소리 울려라~ 종소리 울려~. 따뜻한 벽난로 앞에 예쁜 트리를 세워두고 온 가족이 꾸미는 모습을 TV에서 본 적이 있는데요, 저희 집엔 벽난로도 없고 트리도 없으니 마인크래프트로 
트리를 만들어보겠습니다! 거대 트리 도오~전!

※ 편집자 주
LOL, 오버워치, 배그부터 다양한 인디게임까지 섭렵한 게임 인생 6년차 퓨처킴. 하지만 마인크래프트(이하 마크)는 처음이다. 회사에서 게임하는 게 조금 눈치 보이지만 마크 초고수가 되는 그날까지, 나는 달린다!

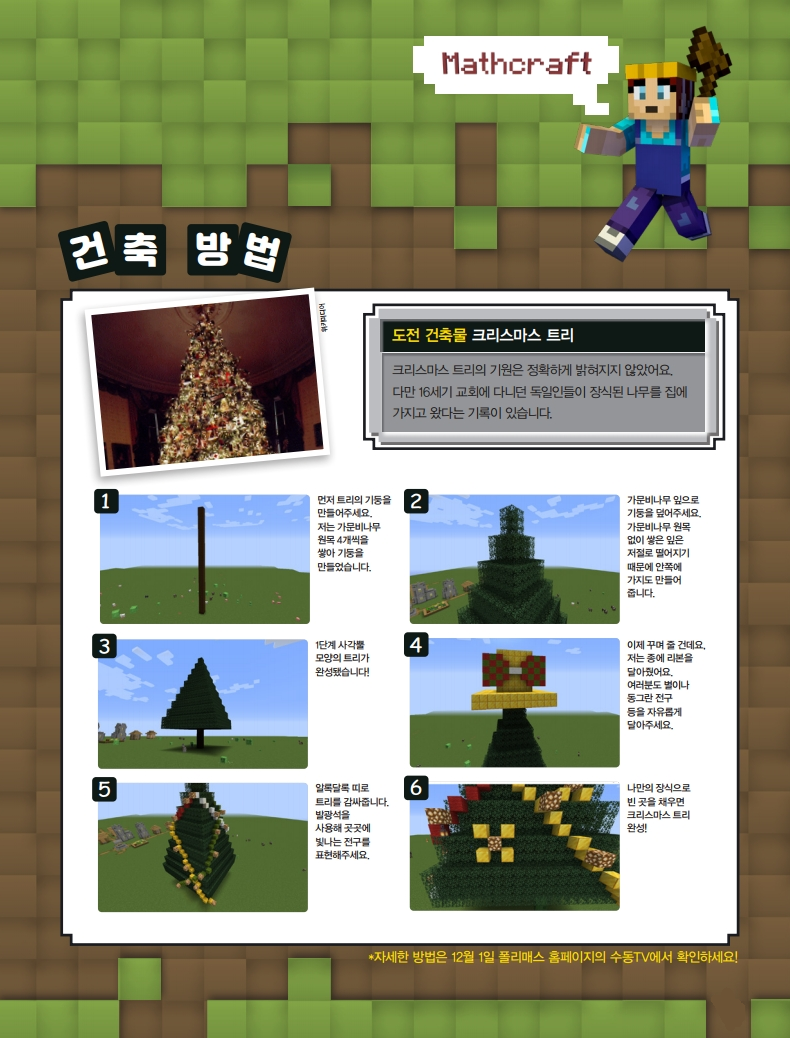
알록달록 예쁜 거대 트리가 완성됐어요. 크리스마스 트리는 주로 침엽수를 사용해 만들어 멀리서 보면 세모 모양이죠. 갑자기 재밌는 도형이 생각나네요. 바로 ‘시에르핀스키 삼각형’이요! 

자기 유사성을 가진 프랙털

위쪽에 보이는 삼각형이 바로 시에르핀스키 삼각형이에요. 이 삼각형은 큰 정삼각형 안에 중간 크기의 정삼각형들이, 또 그 안에 더 작은 정삼각형들이 있는 독특한 구조예요. 폴란드의 수학자 바츠와프 시에르핀스키가 고안했죠. 이렇게 전체 구조와 비슷한 형태의 작은 구조가 계속해서 반복되는 구조를 ‘프랙털’이라고 해요. 

17세기 고트프리트 라이프니츠는 이런 구조를 ‘분수 지수’라고 불렀어요. 이후에도 프랙털과 같은 개념을 언급한 수학자가 있었지만 제각각 다른 이름으로 불렀어요. 그러던 1967년 브누아 망델브로가 영국 해안의 길이를 계산하는 논문에서 ‘프랙털’이라는 표현을 사용하면서 이런 구조를 지칭하는 용어가 프랙털로 굳어지게 됐죠. 프랙털은 자연에서도 많이 찾아볼 수 있는데요, 번개나 나뭇가지 역시 한 갈래로 뻗어가다가 두 갈래로 갈라지는 구조가 반복되는 프랙털이랍니다. 

95쪽 그림을 보며 직접 시에르핀스키 삼각형을 만들어볼까요? 먼저 정삼각형 하나를 그리세요. 그리고 정삼각형의 세 변의 중점을 이어 작은 정삼각형을 만든 다음 새로 그려진 정삼각형을 제거해주세요. 2단계와 같은 모양이 되죠? 이 과정을 계속해서 반복하면 작은 정삼각형이 계속해서 생기는 프랙털 도형을 만들 수 있어요. 

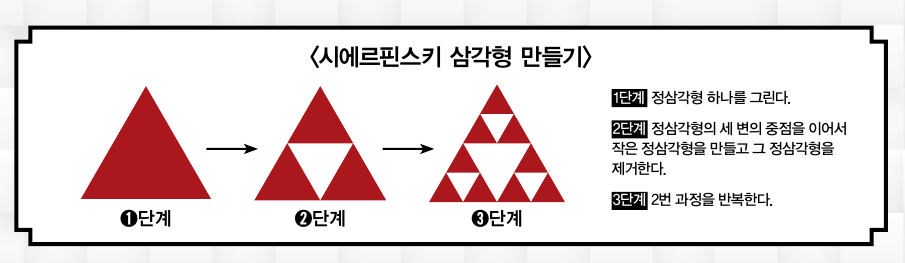
둘레가 무한한 시에르핀스키 삼각형

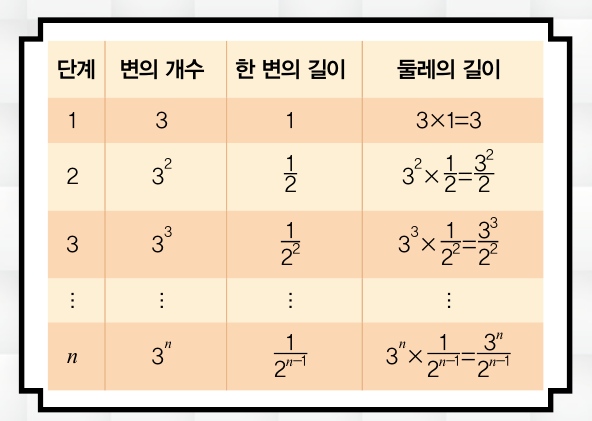
신기한 모양의 시에르핀스키 삼각형은 둘레의 길이가 무한하다는 특징이 있어요. 계산을 통해 왜 그런지 알아볼까요? 단계가 진행될 때마다 정삼각형의 한 변의 길이는 1/2배씩 줄어들고, 변의 개수는 3배씩 늘어나요.

만약 1단계의 정삼각형의 한 변의 길이가 1이라면 2단계 정삼각형의 한 변의 길이는 1/2, 변의 개수는 3×3(=3²)이 돼요. 즉 2단계까지 진행한 시에르핀스키 삼각형의 둘레는 한 변의 길이가 1/2인 변이 3²개 있으므로 3^2/2이죠. 마찬가지로 3단계 정삼각형의 한 변의 길이는 (1/2)², 변의 개수는 3²×3=3³으로 총 둘레는 3³/2²이에요. 결국 n번째 만들어지는 시에르핀스키 삼각형의 둘레는 3ⁿ/2^n-1이고, 단계를 무한히 반복하면 둘레 역시 무한히 커진답니다. 일정한 면적 안에서 무한한 둘레를 갖다니! 정말 신기하죠?

 제가 소개한 프랙털 외에도 다양한 모양의 프랙털을 만들 수 있어요. 이번 크리스마스엔 캐롤을 들으며 나만의 프랙털 트리를 만들어보세요!