d라이브러리

고수들이 심판에게 항의한 건 ‘공정성’ 때문이었습니다. 오늘 대결을 펼칠 종목은 ‘포커’와 ‘15퍼즐’, ‘루빅스 큐브’인데요, 게임을 시작하기 전에 심판이 각 퍼즐을 뒤섞는 걸 본 고수들이 심판에게 “공정하지 않다”며 항의하기 시작한 겁니다. 고수들의 이야기처럼 공정하게 섞는 건 승부에 영향을 줄 만큼 중요한 문제랍니다.

포커나 15퍼즐, 루빅스 큐브 같은 퍼즐은 카드나 퍼즐판을 특정한 순서로 배열한 상태에서 게임을 시작하기 때문에 초기 상태가 승패에 영향을 미칩니다. 예를 들어 포커에서는 카드를 무작위하게 섞지 않으면 한 선수에게만 유리한 카드가 몰릴 수 있죠. 이런 경우 공정한 게임이라고 하기 어렵습니다.

그렇다면 어떻게 해야 공정한 게임이 될까요? 핵심은 고수들이 목소리를 높이는 것처럼 카드와 퍼즐을 최대한 무작위로 섞는 것입니다. 하지만 그냥 무작위라고 하면 좀 모호한 느낌이 드는데요, 각 게임에서 말하는 무작위가 무엇인지 고수들에게 물어보겠습니다.

잠깐! 그런데 카드를 몇 번 섞든지 카드 한 장을 뒤집었을 때 특정 카드가 나올 확률은 이 아니냐고요? 그렇지 않습니다. 5장의 카드로 예를 들어보겠습니다. 

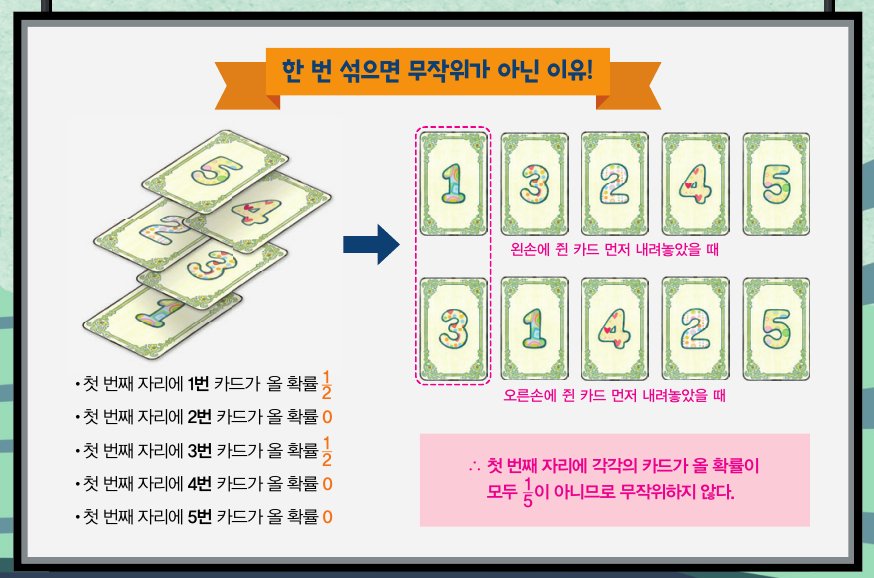
5장의 카드를 왼손과 오른손에 각각 2장, 3장씩 나눠 쥐고 번갈아 내려놓는 방법으로 카드를 섞는다고 생각해보세요. 편의상 왼손에 쥔 카드를 아래부터 1, 2라 하고 오른손의 카드를 아래부터 3, 4, 5라고 하겠습니다. 이 경우 카드를 한 번 섞었을 때 가장 아래와 그 위에 놓이는 카드는 반드시 1 또는 3이 됩니다. 또 세 번째와 네 번째로 놓이는 카드는 2 또는 4가 되죠. 그리고 5는 항상 가장 위에 놓입니다. 즉 한 번 섞었을 때 나올 수 있는 카드의 배열은 아래와 같고, 특정 카드가 나올 ‘확률 분포’가 로 균일하지 않죠. 따라서 무작위라고 할 수 없습니다. 확률 분포란 각 상황에 따른 확률을 나타낸 함수로, 정육면체 주사위의 각 눈이 나올 확률은 모두 이고, 확률 분포 역시 로 균일하죠.

카드를 두 번 섞으면 어떻게 될까요? 처음 섞어서 만든 카드 더미에 붙인 번호를 유지한 채 맨 아래 카드부터 차례로 다시 3장과 2장으로 나눠 쥐고 섞어보겠습니다. 그러면 가장 아래와 바로 위에는 1, 3, 2, 4 중 하나의 카드가 올 수 있습니다. 하지만 모든 카드가 올 수는 없기 때문에 무작위하지 않죠. 한 번 더 섞어야 비로소 모든 카드가 모든 위치에 올 수 있게 됩니다. 3번 이상 섞었을 때 결과적으로 처음과 똑같이 1, 2, 3, 4, 5 순서로 카드가 배열되는 상황이 생기더라도 이 배열은 각 순서에 모든 카드가 똑같은 확률이기 때문에 우연의 일치일 뿐 무작위 배열입니다.