d라이브러리

여러분도 무작위가 퍼즐 대결에서 이렇게 중요한 요소인 줄 모르셨을 겁니다. 그러면 어떻게 해야 퍼즐을 무작위로 섞을 수 있을지 궁금하시죠? 오늘 경기의 심판은 52장의 카드를 둘로 나눠 양손에 쥔 뒤 차례로 교차하며 빠르게 내려놓는 ‘리플 셔플’ 방식으로 카드를 섞었는데요, 이 경우 최소 8번은 리플 셔플을 반복해야 무작위하게 섞을 수 있다는 것이 밝혀졌습니다. 1992년 페르시 다이아코니스 미국 스탠퍼드대학교 수학과 교수가 자세한 증명 과정을 담은 논문을 학술지 ‘응용확률론연보’에 발표했습니다.

리플 셔플을 8번 이상 했을 때 카드가 무작위로 섞인다는 걸 증명하는 과정은 크게 세 단계로 나눌 수 있습니다. 그 과정을 자세히 설명해보겠습니다.

스텝 1) 리플 셔플을 수학 모형으로 나타내자

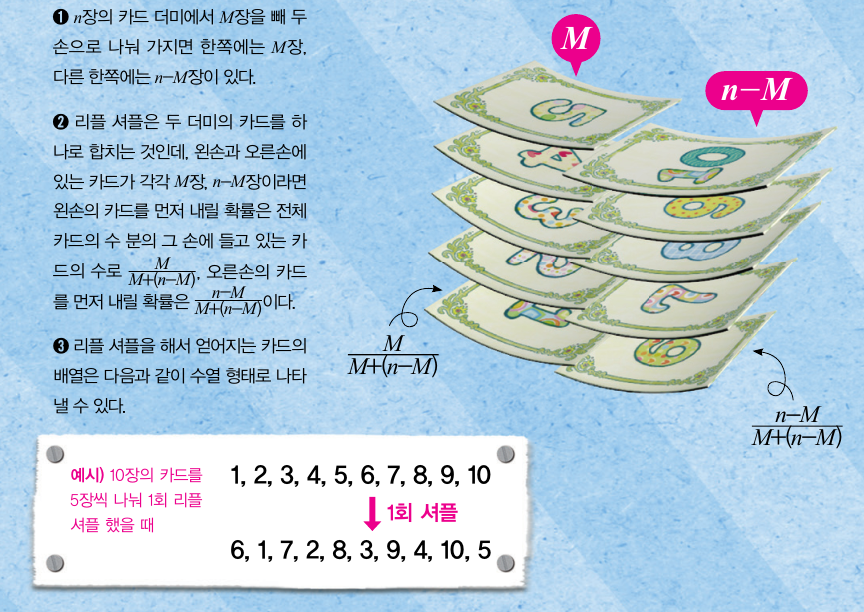
스텝 2) 카드 섞기는 마르코프 연쇄와 똑같다?!

리플 셔플로 카드 섞기를 반복할 때마다 카드의 배열 순서가 다른 수열이 나타난다. 카드 섞기를 t번 했을 때 나타나는 카드 배열의 수열을 변수 X_t라고 하자. 예를 들어 카드 5장을 섞었다고 가정하면 리플 셔플을 반복할 때마다 다음과 같은 수열이 나타난다.

흥미롭게도 이 수열은 X_t+1이 오직 X^_t에 의해서만 결정된다는 특징이 있다. 이처럼 리플 셔플 했을 때 나오는 카드의 배열은 바로 직전 카드 배열에 의해 정해진다. 조금 어렵게 말하면 X_t+1이 가질 수 있는 모든 수열에 대한 확률 분포가 오직 X_t에 의해 결정된다. 그리고 이런 형태의 수열을 ‘마르코프 연쇄’라고 부른다.

마르코프 연쇄는 러시아의 수학자 안드레이 마르코프가 20세기 초에 제시한 개념으로, 확률을 이용해 과거의 정보로부터 미래를 예측하려는 기법이다. 예측이 필요한 거의 모든 분야에서 마르코프 연쇄를 활용하고 있을 정도로 중요한 개념으로 자리 잡았다. 인공지능과 전염병 전파, 야구 통계 분석, 날씨, 인터넷 검색 등 다방면에 쓰이고 있다.

스텝 3) 무작위가 되면 확률분포가 똑같다!

초기 카드 배열을 아는 상태에서는 한 번 섞으면 배열이 어떻게 변할지 대략 예측할 수 있지만 여러번 섞을수록 예측하기가 어렵다. 이 상태를 ‘무작위’라고 한다. 즉 무작위일수록 어떤 순서에 각 카드가 올 확률이 균일하게 1/52 에 가까워지는 것이다. 그럼 모든 카드의 확률이 1/52 인지는 어떻게 알수 있을까?

해법은 마르코프 연쇄의 특징에서 찾을 수 있다. 무작위에 가까우면 마르코프 연쇄의 각 변수가 나타내는 수열의 확률 분포가 거의 일정해진다. 수열의 각 자리에 들어갈 수 있는 수의 후보가 52개로 같아지기 때문이다. 즉 수에 따른 확률 분포 사이의 차이가 0이 되는 것이다. 따라서 무작위로 섞였을 때의 균일한 확률 분포와 섞은 횟수 t에 따른 확률 분포의 차이를 계산해서 그 값이 0에 가까 우면 무작위하다고 볼 수 있다.

반대로 1에 가까우면 아직 무작위하지 않은 것이다. 결국 확률 분포의 차이를 0에 가깝게 해주는 t를 찾으면 몇 번 섞어야 되는지 알 수 있다. 이처럼 확률 분포를 균일하게 만드는 시행 차시(t값)를 찾아주는 방법을 ‘마르코프 연쇄 몬테 카를로(MCMC)’ 기법이라고 부른다.

MCMC는 각 수의 확률 분포가 균일하다는 것을 보장하기 때문에, 동일한 분포를 가지는 표본을 인위적으로 만드는 데 활용된다. 마르코프 연쇄와 마찬가지로 인공 지능과 생물학, 물리학, 기후변화 연구 등 다양한 분야에 쓰인다.

드를 무작위하게 섞는 수학적인 원리, 이제 이해하셨나요? 그렇다면 MCMC 기법으로 찾아낸 무작위를 보장하는 카드 섞어주기 횟수는 몇 번일까요? 다이아코니스 교수는 카드가 52 장인 트럼프 카드의 경우 4.5회에서 12.5회 사이에서 무작위화가 일어난다는 것을 알아냈습 니다. 계산 결과를 그래프로 그려보면 6~8회 사이에서 값이 급격하게 작아집니다.

따라서 최소 7회 또는 8회 이상 섞으면 카드가 무작위하게 뒤섞이기 시작했다고 볼 수 있습 니다. 이때 횟수를 정하는 기준은 7~12회 사이에서 주관적으로 정합니다. 어떤 값이 0에 가깝다고 볼 수 있느냐에 따라서 7회만 섞어도 충분히 무작위하다고 볼 수도 있고, 12회까지 섞어야 엄밀하게 무작위하다고 판단할 수도 있습니다.

그 이유는 판단 기준이 되는 값이 ‘확률’이기 때문입니다. 예를 들어 주사위 던지기 시행을 여러 번 시도할 때 각 눈이 나올 확률인 1/6 로 딱 떨어져 나오지 않고 시행을 무한히 반복할 때 1/6에 가까워집니다. 마찬가지로 카드 섞기에서도 시행을 아주 많이 할 때 1/52 에 가까워지는데 무한히 섞을 수 없으니 어느 정도의 값에 가까워지면 무작위하다고 인정하자는 것이죠. 이 연구가 발표
된 뒤부터 포커 대결에서 트럼프 카드를 섞을 때 7번 이상 충분히 섞는 것으로 규칙이 바뀌었습니다.